一元配置分散分析 なじみのない用語かも知れないが,「独立 k 標本の平均値の差の検定」である。 残念なことに,Julia では標準的に用意されておらず,GitHab には何例かあるものの,全ての人が簡単にアクセスできるものではないかもしれないので,あえてプログラムを書き,公開してみたい。 まず最初の関数は,測定データ x とそのデータがどの群に属するかを表す g で検定を行うという onewayAnova 関数である。 Julia> using Statistics, Distributions Julia> function onewayAnova(x, g; var_equal=false) Julia> member = Set(g) Julia> k = length(member) Julia> gi = [] Julia> ni = [] Julia> mi = [] Julia> vi = [] Julia> for i in member Julia> append!(gi, i) Julia> append!(ni, sum(g .== i)) Julia> append!(mi, mean(x[g .== i])) Julia> append!(vi, var(x[g .== i])) Julia> end Julia> method = "One-way analysis of means" Julia> if var_equal Julia> n = sum(ni) Julia> mx = mean(x) Julia> df1, df2 = k - 1, n - k Julia> F = ((sum(ni .* (mi .- mx).^2) / df1) / (sum((ni .- 1) .* vi) / df2)) Julia> else Julia> method *= " (not assuming equal variances)" Julia> wi = ni ./ vi Julia> sum_wi = sum(wi) Julia> tmp = sum((1 .- wi ./ sum_wi).^2 ./ (ni .- 1)) ./ (k^2 - 1) Julia> m = sum(wi .* mi) / sum_wi Julia> df1, df2 = k - 1, 1 / (3 * tmp) Julia> F = sum(wi .* (mi .- m).^2) / (df1 * (1 + 2 * (k - 2) * tmp)) Julia> end Julia> order = sortperm(gi) Julia> gi = gi[order] Julia> ni = ni[order] Julia> mi = mi[order] Julia> vi = vi[order] Julia> output1(gi, ni, mi, vi) Julia> output2(method, F, df1, df2) Julia> end onewayAnova (generic function with 2 methods) もう一つの関数は,なんと,同じ名前 onewayAnova であるが,引数(の型と個数)が違う。 Julia は,同じ名前の関数があると,呼ばれたのはどの関数だろう?と判断して,適切な関数を呼んでくれる。 なんと,賢い!! Julia> function onewayAnova(ni, mi, ui, gi; var_equal=false) Julia> x = [] Julia> g = [] Julia> for i in 1:length(ni) Julia> obj = Normal(mi[i], sqrt(ui[i])) Julia> temp = rand(obj, ni[i]) Julia> temp = (temp .- mean(temp)) ./ std(temp) .* sqrt(ui[i]) .+ mi[i] Julia> append!(x, temp) Julia> append!(g, repeat([gi[i]], ni[i])) Julia> end Julia> ve = var_equal Julia> onewayAnova(x, g, var_equal=ve) Julia> end onewayAnova (generic function with 2 methods) 次の 2 つの関数は,検定の結果を出力するための関数である。 Julia> using Printf Julia> function output1(gi, ni, mi,vi) Julia> println("Sumary of the data.") Julia> @printf("%10s: %5s %15s %15s %15s\n", "group", "n", "mean", "variance", "s.d.") Julia> for i = 1:length(gi) Julia> @printf("%10s: %5d %15.7f %15.7f %15.7f\n", gi[i], ni[i], mi[i], vi[i], sqrt(vi[i])) Julia> end Julia> end Julia> function output2(method, F, df1, df2) Julia> println(method) Julia> obj = FDist(df1, df2) Julia> if df2 == floor(df2) Julia> @printf("F = %.7g, d.f.1 = %d, d.f.2 = %d, p value = %.7g\n", F, df1, df2, 1 - cdf(obj, F)) Julia> else Julia> @printf("F = %.7g, d.f.1 = %d, d.f.2 = %.7g, p value = %.7g\n", F, df1, df2, 1 - cdf(obj, F)) Julia> end Julia> end output2 (generic function with 1 method) 使用例 最初の使用例は,データベクトルと,群データベクトルを用いて呼び出すものである。 まず,R ではデフォルトではないが,群の分散が等しいと仮定する場合である。 Julia> # > x = c(2, 1, 2, 3, 4, 3, 5, 4, 6, 7, 2, 4) Julia> # > g = c("a", "a", "a", "a", "b", "c", "c", "b", "b", "c", "c", "c") Julia> # > oneway.test(x ~ g, var.equal=TRUE) Julia> # Julia> # One-way analysis of means Julia> # Julia> # data: x and g Julia> # F = 3.5715, num df = 2, denom df = 9, p-value = 0.07214 Julia> ##### Julia> x = [2, 1, 2, 3, 4, 3, 5, 4, 6, 7, 2, 4] Julia> g = ["a", "a", "a", "a", "b", "c", "c", "b", "b", "c", "c", "c"] Julia> onewayAnova(x, g, var_equal=true) Sumary of the data. group: n mean variance s.d. a: 4 2.0000000 0.6666667 0.8164966 b: 3 4.6666667 1.3333333 1.1547005 c: 5 4.2000000 3.7000000 1.9235384 One-way analysis of means F = 3.57149, d.f.1 = 2, d.f.2 = 9, p value = 0.0721381 次の使用例は,同じデータに対して,群の分散が等しいことを仮定しない場合(独立 2 標本の t 検定の場合の,Welch の方法の拡張)である。 これは R ではデフォルトになっている。 Julia> # > oneway.test(x ~ g) Julia> # Julia> # One-way analysis of means (not Julia> # assuming equal variances) Julia> # Julia> # data: x and g Julia> # F = 6.2568, num df = 2.0000, denom df = 5.0833, p-value = 0.04259 Julia> ##### Julia> onewayAnova(x, g) Sumary of the data. group: n mean variance s.d. a: 4 2.0000000 0.6666667 0.8164966 b: 3 4.6666667 1.3333333 1.1547005 c: 5 4.2000000 3.7000000 1.9235384 One-way analysis of means (not assuming equal variances) F = 6.256838, d.f.1 = 2, d.f.2 = 5.083311, p value = 0.04258988 二番目の例は,群ごとに,「サンプルサイズ」,「平均値」,「不偏分散」,「群の識別子」を与えて検定を行う方法である。 Julia> onewayAnova([4, 3, 5], [2, 4.6666667, 4.2], [0.6666667, 1.3333333, 3.7], ["a", "b", "c"], var_equal=true) Sumary of the data. group: n mean variance s.d. a: 4 2.0000000 0.6666667 0.8164966 b: 3 4.6666667 1.3333333 1.1547005 c: 5 4.2000000 3.7000000 1.9235384 One-way analysis of means F = 3.57149, d.f.1 = 2, d.f.2 = 9, p value = 0.07213809 同じデータで,等分散を仮定しない場合である。 Julia> onewayAnova([4, 3, 5], [2, 4.6666667, 4.2], [0.6666667, 1.3333333, 3.7], ["a", "b", "c"]) Sumary of the data. group: n mean variance s.d. a: 4 2.0000000 0.6666667 0.8164966 b: 3 4.6666667 1.3333333 1.1547005 c: 5 4.2000000 3.7000000 1.9235384 One-way analysis of means (not assuming equal variances) F = 6.256838, d.f.1 = 2, d.f.2 = 5.083311, p value = 0.04258988
1. Julia の F 分布関数
Rmath パッケージを使用すれば,R の pf(), qf() が使える。第 4 引数は lower.tail に対応し,true (デフォルト)のとき lower.tail=TRUE,false のとき lower.tail=FALSE を意味する。
using Distributions, Rmath
1.1. オブジェクト生成 FDist( )
obj = FDist(3, 10)
FDist{Float64}(ν1=3.0, ν2=10.0)
1.2. 上側確率 ccdf( ), pf( )
ccdf(obj, 1.5)
0.2737765559785967
pf(1.5, 3, 10, false)
0.2737765559785967
1.3. 上側確率に対するパーセント点 cquantile( ), qf( )
cquantile(obj, 0.05)
3.7082648190468457
qf(0.05, 3, 10, false)
3.7082648190468457
1. Julia の t 分布関数
Rmath パッケージを使用すれば,R の pt(), qt() が使える。第 3 引数は lower.tail に対応し,true (デフォルト)のとき lower.tail=TRUE,false のとき lower.tail=FALSE を意味する。
using Distributions, Rmath
1.1. オブジェクト生成 TDist(ν)
obj10 = TDist(10)
TDist{Float64}(ν=10.0)
1.2. 確率
1.2.1. 上側確率 ccdf( ), pt( )
ccdf(obj10, 1.96)
0.03921812012384987
pt(1.96, 10, false)
0.03921812012384987
1.2.2. Julia 下側確率 cdf( ), pt( )
cdf(obj10, -1.96)
0.03921812012384987
pt(-1.96, 10)
0.03921812012384987
1.3. パーセント点
1.3.1. 上側確率に対するパーセント点 cquantile( ), qt( )
cquantile(obj10, 0.025)
2.2281388519862744
qt(0.025, 10, false)
2.2281388519862744
1.3.2. 下側確率に対するパーセント点 quantile( ), qt( )
quantile(obj10, 0.025)
-2.2281388519862744
qt(0.025, 10)
-2.2281388519862744
1. Julia のカイ二乗分布関数
Rmath パッケージを使用すれば,R の pchisqt(), qchisq() が使える。第 2 引数は lower.tail に対応し,true (デフォルト)のとき lower.tail=TRUE,false のとき lower.tail=FALSE を意味する。
using Distributions, Rmath
1.1. オブジェクト生成
obj1 = Chisq(1)
Chisq{Float64}(ν=1.0)
1.2. 上側確率
ccdf(obj1, 3.841459)
0.04999999465319573
pchisq(3.841459, 1, false)
0.04999999465319573
1.3. 上側確率に対するパーセント点
cquantile(obj1, 0.05)
3.841458820694126
qchisq(0.05, 1, false)
3.841458820694126
(@v1.5) pkg> add Distributions, Random, HypothesisTests
julia> using Distributions, Random, HypothesisTests
分布関数
標準正規分布において,R の rnorm, pnorm, qnorm, dnorm に相当するもの
Julia の場合は,「オブジェクト」を操作する。
まず,標準正規分布のオブジェクトを作る。
julia> obj = Normal()
Normal{Float64}(μ=0.0, σ=1.0)
乱数生成
正規乱数 500 個を生成する。
R では
> d = rnorm(500)
Julia では
julia> d = rand(obj, 500);
生成された乱数データについて,平均値,不偏分散,標準偏差を計算してみる。
julia> println("mean = $(mean(d)), var = $(var(d)), sd = $(std(d))")
mean = -0.025412744391597998, var = 0.9232796228593824, sd = 0.9608744053513875
下側確率
R では
> pnorm(1.96)
[1] 0.9750021
Julia では
julia> cdf(obj, 1.96)
0.9750021048517795
複数の引数(ベクトル)において,各要素についての結果は,ドット記法 'cdf.(' を使って書ける。
R では
> pnorm(c(-1.96, 0, 1.96))
[1] 0.0249979 0.5000000 0.9750021
Julia では
julia> cdf.(obj, [-1.96, 0, 1.96])
3-element Array{Float64,1}:
0.024997895148220435
0.5
0.9750021048517795
パーセント点
R では
> qnorm(c(0.025, 0.5, 0.975))
[1] -1.959964 0.000000 1.959964
Julia では
julia> quantile(obj, [0.025, 0.5, 0.975])
3-element Array{Float64,1}:
-1.9599639845400592
0.0
1.9599639845400583
確率密度
R では
> dnorm(c(-1.96, 0, 1.96))
[1] 0.05844094 0.39894228 0.05844094
Julia では
julia> pdf.(obj, [-1.96, 0, 1.96])
3-element Array{Float64,1}:
0.05844094433345147
0.3989422804014327
0.05844094433345147
等分散を仮定した独立 2 標本の平均値の差の検定
両側検定
R では
> x = c(3,2,1,2,3,2,1,2,3,4,3,2,2,3,4)
> y = c(3,2,1,2,3,2,3,4,4,3,3,3,2,2,3,3,4,5)
> t.test(x, y, var.equal=TRUE)
Two Sample t-test
data: x and y
t = -1.282, df = 31, p-value = 0.2093
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-1.0939215 0.2494771
sample estimates:
mean of x mean of y
2.466667 2.888889
Julia では
julia> x = [3,2,1,2,3,2,1,2,3,4,3,2,2,3,4];
julia> y = [3,2,1,2,3,2,3,4,4,3,3,3,2,2,3,3,4,5];
julia> obj = EqualVarianceTTest(x, y)
Two sample t-test (equal variance)
----------------------------------
Population details:
parameter of interest: Mean difference
value under h_0: 0
point estimate: -0.422222
95% confidence interval: (-1.0939, 0.2495)
Test summary:
outcome with 95% confidence: fail to reject h_0
two-sided p-value: 0.2093
Details:
number of observations: [15,18]
t-statistic: -1.2820140381935845
degrees of freedom: 31
empirical standard error: 0.32934290081343587
片側検定
R で,alternative="less"
> t.test(x, y, var.equal=TRUE, alternative="less")
Two Sample t-test
data: x and y
t = -1.282, df = 31, p-value = 0.1047
alternative hypothesis: true difference in means is less than 0
95 percent confidence interval:
-Inf 0.1361849
sample estimates:
mean of x mean of y
2.466667 2.888889
Julia では
julia> println(pvalue(obj, tail=:left))
0.10467146197969886
R で,alternative="greater"
> t.test(x, y, var.equal=TRUE, alternative="greater")
Two Sample t-test
data: x and y
t = -1.282, df = 31, p-value = 0.8953
alternative hypothesis: true difference in means is greater than 0
95 percent confidence interval:
-0.9806293 Inf
sample estimates:
mean of x mean of y
2.466667 2.888889
Julia では
julia> println(pvalue(obj, tail=:right))
0.8953285380203011
その他の検定手法
OneSampleTTest(x)
EqualVarianceTTest(x, y)
UnequalVarianceTTest(x, y)
ChisqTest(matrix)
これ以外は,GitHub にあったりするが,最悪,自分で書かねばならない。かな?
Julia で CSV ファイルを読む。あるいは,データフレームを使う。
まずは,CSV と DataFrames パッケージのインストール。
(@v1.5) pkg> add CSV, DataFrames
Updating registry at `~/.julia/registries/General`
######################################################################## 100.0%
Resolving package versions...
Installed PooledArrays ─── v0.5.3
Installed SentinelArrays ─ v1.2.16
Installed CSV ──────────── v0.8.2
Updating `~/.julia/environments/v1.5/Project.toml`
[336ed68f] + CSV v0.8.2
Updating `~/.julia/environments/v1.5/Manifest.toml`
[336ed68f] + CSV v0.8.2
[2dfb63ee] + PooledArrays v0.5.3
[91c51154] + SentinelArrays v1.2.16
Resolving package versions...
Installed InvertedIndices ─── v1.0.0
Installed StructTypes ─────── v1.2.1
Installed CategoricalArrays ─ v0.9.0
Installed DataFrames ──────── v0.22.2
Installed PrettyTables ────── v0.10.1
Updating `~/.julia/environments/v1.5/Project.toml`
[a93c6f00] + DataFrames v0.22.2
Updating `~/.julia/environments/v1.5/Manifest.toml`
[324d7699] + CategoricalArrays v0.9.0
[a93c6f00] + DataFrames v0.22.2
[41ab1584] + InvertedIndices v1.0.0
[08abe8d2] + PrettyTables v0.10.1
[856f2bd8] + StructTypes v1.2.1
[9fa8497b] + Future
そして,using CSV, DataFrames。初回はコンパイルを伴うので,少しばかり時間がかかる。
julia> using CSV, DataFrames
[ Info: Precompiling CSV [336ed68f-0bac-5ca0-87d4-7b16caf5d00b]
[ Info: Precompiling DataFrames [a93c6f00-e57d-5684-b7b6-d8193f3e46c0]
読み込むデータがどこにあるか,確認しておくこと。
必要なら working directory を変更しておく。
julia> cd("/Users/foor/bar/")
julia> @time df = CSV.read("test.csv", DataFrame);
9.007682 seconds (49.06 k allocations: 1.257 GiB, 1.77% gc time)
実行時間測定のために @time を付けたが,必要なければ取る。
対話モードでやるときは,最後の ';' を付けておく方がいいかもしれない。
R の data.table::fread() では 5.027 sec. であったので,ちょっと負けるなあ。
でも,Python でも 28.793 sec. なので,よしとしよう。
julia> row, col = size(df) # データフレームのサイズ
(100000, 1500)
データフレームの最初の方の確認
julia> first(df, 5)
5×1500 DataFrame
Row │ X1 X2 X3 X4 ⋯
│ Float64 Float64 Float64 Float64
────┼──────────────────────────────────────
1 │ 51.26 44.35 38.61 36.61
2 │ 41.03 59.43 48.48 59.44
3 │ 61.89 29.32 64.51 51.07
4 │ 56.88 59.77 49.92 48.76
5 │ 69.43 56.75 65.3 47.28 ⋯
1488 columns omitted
データフレームの最後の方の確認
julia> last(df, 5)
5×1500 DataFrame
Row │ X1 X2 X3 X4 ⋯
│ Float64 Float64 Float64 Float64
────┼──────────────────────────────────────
1 │ 48.05 58.57 44.79 56.38
2 │ 79.41 41.44 53.72 52.31
3 │ 61.82 48.27 60.91 36.46
4 │ 49.19 24.26 49.97 44.7
5 │ 51.66 66.37 56.99 55.78 ⋯
1488 columns omitted
1 列目(変数名: "X1") の指定法
julia> sum(df[!, 1]) # 列番号で指定
5.004236609999999e6
julia> sum(df[!, "X1"]) # 変数名で指定 その1 df[!, 1],df[!, :1] も同じ
5.004236609999999e6
julia> sum(df.X1) # 変数名で指定 その2 df.X1 でも同じ
5.004236609999999e6
df[!, [:X1]] と df[:, [:X1]] はデータフレームだが,df[!, :X1] と df[:, :X1] はベクトル
df[!, "X1"] はコピーを作らない,df[:, "X1"] はコピーを作る
julia> df[!, "X1"] === df[:, "X1"] # === は同一かどうか(メモリー上で同じ位置にあるもの)
false
julia> df[!, "X1"] == df[:, "X1"] # == は等しいかどうか
true
julia> df[:, [:X2, :X5]]
100000×2 DataFrame
Row │ X2 X5
│ Float64 Float64
────────┼──────────────────
1 │ 44.35 54.22
2 │ 59.43 44.9
3 │ 29.32 34.25
4 │ 59.77 43.93
以上の他にも何種類かある。
行の抽出
julia> df2 = df[15:36, :]
22×1500 DataFrame
Row │ X1 X2 X3 ⋯
│ Float64 Float64 Float64 ⋯
────┼───────────────────────────────
1 │ 58.78 39.62 72.1 ⋯
2 │ 46.84 59.54 46.05 ⋯
:
22 │ 69.09 54.01 54.76
julia> size(df2)
(22, 1500)
抽出と同時に並べ替えもできる。
julia> df3 = df[[5, 2, 7], :]
3×1500 DataFrame
Row │ X1 X2 X3
│ Float64 Float64 Float64
────┼───────────────────────────
1 │ 69.43 56.75 65.3 ⋯
2 │ 41.03 59.43 48.48
3 │ 44.68 59.1 51.65
julia> size(df3)
(3, 1500)
列の抽出
julia> df4 = df[:, ["X1", "X5", "X2"]]
100000×3 DataFrame
Row │ X1 X5 X2
│ Float64 Float64 Float64
────────┼───────────────────────────
1 │ 51.26 54.22 44.35
2 │ 41.03 44.9 59.43
3 │ 61.89 34.25 29.32
4 │ 56.88 43.93 59.77
:
julia> size(df4)
(100000, 3)
行と列を同時に抽出
上の応用。
julia> df5 = df[[10, 5, 3], ["X1", "X5", "X2"]]
3×3 DataFrame
Row │ X1 X5 X2
│ Float64 Float64 Float64
─────┼───────────────────────────
1 │ 49.09 56.05 45.22
2 │ 69.43 45.76 56.75
3 │ 61.89 34.25 29.32
julia> size(df5)
(3, 3)
条件を満たす行の抽出
julia> df6 = df[df.X1 .> 87, ["X2", "X6", "X9"]] # > 前のピリオドを忘れないように
9×3 DataFrame
Row │ X2 X6 X9
│ Float64 Float64 Float64
─────┼───────────────────────────
1 │ 55.27 59.61 64.16
2 │ 38.27 38.72 41.42
3 │ 38.24 53.88 29.97
該当セルへの代入
行と列の指定法がわかれば,該当セルへの代入も同じように行えることがわかる。
julia> df7[1, 2] = 99999
99999
julia> df7
4×4 DataFrame
Row │ X6 X4 X1 X2
│ Float64 Float64 Float64 Float64
─────┼───────────────────────────────────
1 │ 38.72 99999.0 90.19 38.27
2 │ 49.75 49.8 89.25 64.74
3 │ 70.82 24.25 89.77 42.46
4 │ 34.49 54.26 92.58 55.82
列全部を代入対象とすることもできる。'.=' に注意。
julia> df7[!, 1] .= 77777
4-element Array{Int64,1}:
77777
77777
77777
77777
julia> df7
4×4 DataFrame
Row │ X6 X4 X1 X2
│ Int64 Float64 Float64 Float64
─────┼───────────────────────────────────
1 │ 77777 99999.0 90.19 38.27
2 │ 77777 49.8 89.25 64.74
3 │ 77777 24.25 89.77 42.46
4 │ 77777 54.26 92.58 55.82
並べ替え(ソート)
列を基準としてソートする。
julia> df8 = CSV.sort(df7, :X1)
4×4 DataFrame
Row │ X6 X4 X1 X2
│ Int64 Float64 Float64 Float64
─────┼───────────────────────────────────
1 │ 77777 49.8 89.25 64.74
2 │ 77777 24.25 89.77 42.46
3 │ 77777 99999.0 90.19 38.27
4 │ 77777 54.26 92.58 55.82
統計解析
julia> describe(df)
1500×7 DataFrame
Row │ variable mean min median max nmissing eltype
│ Symbol Float64 Float64 Float64 Float64 Int64 DataType
──────┼──────────────────────────────────────────────────────────────────
1 │ X1 50.0424 6.38 50.01 92.58 0 Float64
2 │ X2 49.9949 3.97 50.02 90.16 0 Float64
3 │ X3 50.0425 6.8 50.03 92.79 0 Float64
:
julia> combine(df, names(df) .=> sum)
1×1500 DataFrame
Row │ X1_sum X2_sum X3_sum X4_sum ⋯
│ Float64 Float64 Float64 Float64 ⋯
────┼───────────────────────
1 │ 5.00424e6 4.99949e6 5.00425e6 5.00398e6 ⋯
julia> sum(df.X2) # 合計
4.99949053e6
julia> var(df.X3) # 不偏分散
99.8737108092948
julia> var(df.X3, corrected=false) # 分散
99.87271207218672
julia> std(df.X4) # 標準偏差
10.012003767127581
julia> cor(df.X1, df.X3) # ピアソンの積率相関係数
-0.0027621173217232155
julia> using StatsBase
[ Info: Precompiling StatsBase [2913bbd2-ae8a-5f71-8c99-4fb6c76f3a91]
julia> corspearman(df.X1, df.X3) # スピアマンの順位相関係数
-0.0033731070923354164
julia> corkendall(df.X1, df.X3) # ケンドールの順位相関係数
-0.002256851537930442
散布図
julia> xy = df[:, [:X1, :X2]]
100000×2 DataFrame
Row │ X1 X2
│ Float64 Float64
────────┼──────────────────
1 │ 51.26 44.35
2 │ 41.03 59.43
3 │ 61.89 29.32
4 │ 56.88 59.77
:
julia> plot(df.X1, df.X2, st=:scatter, xlabel="X1", ylabel="X2", label="", title="scattergram")

ヒートマップ
julia> using StatsBase
julia> using Plots
julia> fit(Histogram, (df.X1, df.X2)) |> Plots.plot

単回帰分析
julia> using GLM
julia> ols = lm(@formula(X2 ~ X1), df)
StatsModels.TableRegressionModel{LinearModel{GLM.LmResp{Array{Float64,1}},GLM.DensePredChol{Float64,LinearAlgebra.Cholesky{Float64,Array{Float64,2}}}},Array{Float64,2}}
X2 ~ 1 + X1
Coefficients:
─────────────────────────────────────────────────────────────────────────────────
Coef. Std. Error t Pr(>|t|) Lower 95% Upper 95%
─────────────────────────────────────────────────────────────────────────────────
(Intercept) 50.0038 0.161703 309.23 <1e-99 49.6868 50.3207
X1 -0.000177375 0.00316896 -0.06 0.9554 -0.00638851 0.00603376
─────────────────────────────────────────────────────────────────────────────────
重回帰分析
julia> ols = lm(@formula(X2 ~ X1 + X3 + X10), df)
StatsModels.TableRegressionModel{LinearModel{GLM.LmResp{Array{Float64,1}},GLM.DensePredChol{Float64,LinearAlgebra.Cholesky{Float64,Array{Float64,2}}}},Array{Float64,2}}
X2 ~ 1 + X1 + X3 + X10
Coefficients:
─────────────────────────────────────────────────────────────────────────────────
Coef. Std. Error t Pr(>|t|) Lower 95% Upper 95%
─────────────────────────────────────────────────────────────────────────────────
(Intercept) 49.63 0.275956 179.85 <1e-99 49.0892 50.1709
X1 -0.000161144 0.00316895 -0.05 0.9594 -0.00637226 0.00604997
X3 0.00151638 0.00316354 0.48 0.6317 -0.00468412 0.00771688
X10 0.00594262 0.00316205 1.88 0.0602 -0.000254952 0.0121402
─────────────────────────────────────────────────────────────────────────────────
回帰分析のまとめ
julia> response(ols) # 従属変数
100000-element Array{Float64,1}:
44.35
59.43
29.32
59.77
56.75
33.05
:
julia> coeftable(ols)
──────────────────────────────────────────────────────────────────────────────────
Coef. Std. Error t Pr(>|t|) Lower 95% Upper 95%
─────────────────────────────────────────────────────────────────────────────────
(Intercept) 49.63 0.275956 179.85 <1e-99 49.0892 50.1709
X1 -0.000161144 0.00316895 -0.05 0.9594 -0.00637226 0.00604997
X3 0.00151638 0.00316354 0.48 0.6317 -0.00468412 0.00771688
X10 0.00594262 0.00316205 1.88 0.0602 -0.000254952 0.0121402
─────────────────────────────────────────────────────────────────────────────────
julia> coefnames(ols) # 独立変数の名前
4-element Array{String,1}:
"(Intercept)"
"X1"
"X3"
"X10"
julia> coef(ols) # 回帰係数
4-element Array{Float64,1}:
49.63004506573552
-0.00016114387378327575
0.0015163795173625358
0.005942618126945406
julia> stderror(ols) # 偏回帰係数の標準誤差
4-element Array{Float64,1}:
0.2759555477601921
0.00316895479304485
0.003163542394883129
0.00316204541408164
julia> round.(stderror(ols), digits=5)
4-element Array{Float64,1}:
0.27596
0.00317
0.00316
0.00316
julia> vcov(ols) # 偏回帰係数の分散・共分散行列
4×4 Array{Float64,2}:
0.0761515 -0.000504924 -0.000499421 -0.000497993
-0.000504924 1.00423e-5 2.75781e-8 2.00964e-8
-0.000499421 2.75781e-8 1.0008e-5 -5.57047e-8
-0.000497993 2.00964e-8 -5.57047e-8 9.99853e-6
julia> confint(ols) # 回帰係数の信頼区間
4×2 Array{Float64,2}:
49.0892 50.1709
-0.00637226 0.00604997
-0.00468412 0.00771688
-0.000254952 0.0121402
julia> predict(ols) # 予測値
100000-element Array{Float64,1}:
49.97502667684598
49.998951264807296
50.010448604441656
49.95823034383087
50.04644378530134
50.04986504302499
50.0524343170104
:
julia> round.(predict(ols), digits=5)
100000-element Array{Float64,1}:
49.97503
49.99895
50.01045
49.95823
50.04644
50.04987
:
julia> residuals(ols) # 残差
100000-element Array{Float64,1}:
-5.625026676845977
9.431048735192704
-20.690448604441656
9.811769656169133
6.703556214698658
-16.99986504302499
:
julia> r2(ols) # 決定係数
3.775037972164608e-5
julia> adjr2(ols) # 自由度調整済み R2 R とちょっと値が異なる
7.75031223032574e-6
julia> aic(ols) # AIC
744259.4650342457
julia> aicc(ols) # 調整済み AIC
744259.4656342817
julia> bic(ols) # BIC
744307.0296615706
julia> loglikelihood(ols) # 対数尤度
-372124.7325171229
julia> deviance(ols) # デビアンス
9.994475506014155e6
julia> nulldeviance(ols) # ヌル・デビアンス
9.994852815503202e6
julia> nobs(ols) # 分析に用いたサンプルサイズ
100000.0
julia> dof(ols) # 独立変数の個数 + 2
5
julia> dof_residual(ols) # 残差の自由度
99996.0
ヒストグラム(度数分布)
julia> fit(Histogram, df.X1)
Histogram{Int64,1,Tuple{StepRangeLen{Float64,Base.TwicePrecision{Float64},Base.TwicePrecision{Float64}}}}
edges:
5.0:5.0:95.0
weights: [2, 16, 93, 465, 1616, 4403, 9067, 15026, 19263, 19100, 14993, 9225, 4447, 1603, 540, 121, 18, 2]
closed: left
isdensity: false
julia> fit(Histogram, df.X1, nbins=10)
Histogram{Int64,1,Tuple{StepRangeLen{Float64,Base.TwicePrecision{Float64},Base.TwicePrecision{Float64}}}}
edges:
0.0:10.0:100.0
weights: [2, 109, 2081, 13470, 34289, 34093, 13672, 2143, 139, 2]
closed: left
isdensity: false
julia> using Plots
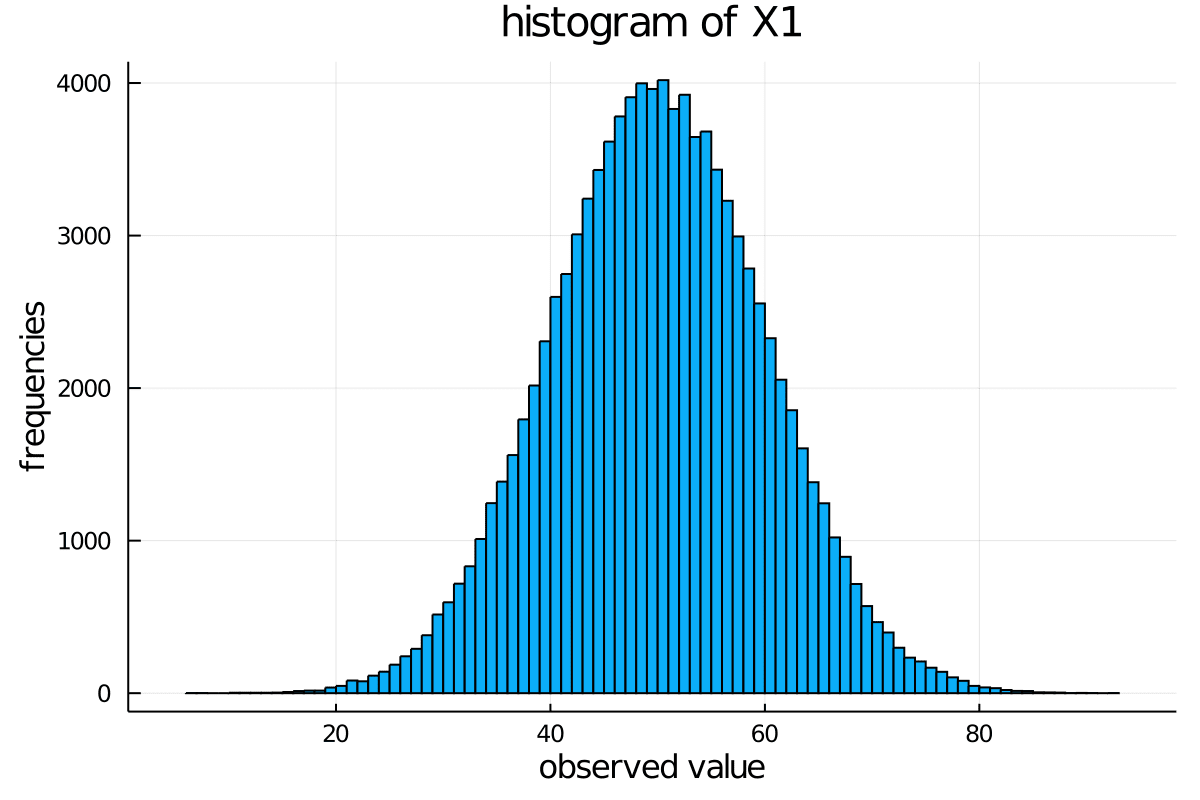
julia> plot(df.X1, st=:histogram, label="", xlabel="observed value", ylabel="frequencies", title="histogram of X1")
Julia で CSV ファイルを読む。あるいは,データフレームを使う。
まずは,CSV と DataFrames パッケージのインストール。
(@v1.5) pkg> add CSV, DataFrames
Updating registry at `~/.julia/registries/General`
######################################################################## 100.0%
Resolving package versions...
Installed PooledArrays ─── v0.5.3
Installed SentinelArrays ─ v1.2.16
Installed CSV ──────────── v0.8.2
Updating `~/.julia/environments/v1.5/Project.toml`
[336ed68f] + CSV v0.8.2
Updating `~/.julia/environments/v1.5/Manifest.toml`
[336ed68f] + CSV v0.8.2
[2dfb63ee] + PooledArrays v0.5.3
[91c51154] + SentinelArrays v1.2.16
Resolving package versions...
Installed InvertedIndices ─── v1.0.0
Installed StructTypes ─────── v1.2.1
Installed CategoricalArrays ─ v0.9.0
Installed DataFrames ──────── v0.22.2
Installed PrettyTables ────── v0.10.1
Updating `~/.julia/environments/v1.5/Project.toml`
[a93c6f00] + DataFrames v0.22.2
Updating `~/.julia/environments/v1.5/Manifest.toml`
[324d7699] + CategoricalArrays v0.9.0
[a93c6f00] + DataFrames v0.22.2
[41ab1584] + InvertedIndices v1.0.0
[08abe8d2] + PrettyTables v0.10.1
[856f2bd8] + StructTypes v1.2.1
[9fa8497b] + Future
そして,using CSV, DataFrames。初回はコンパイルを伴うので,少しばかり時間がかかる。
julia> using CSV, DataFrames
[ Info: Precompiling CSV [336ed68f-0bac-5ca0-87d4-7b16caf5d00b]
[ Info: Precompiling DataFrames [a93c6f00-e57d-5684-b7b6-d8193f3e46c0]
読み込むデータがどこにあるか,確認しておくこと。
必要なら working directory を変更しておく。
julia> cd("/Users/foor/bar/")
julia> @time df = CSV.read("test.csv", DataFrame);
9.007682 seconds (49.06 k allocations: 1.257 GiB, 1.77% gc time)
実行時間測定のために @time を付けたが,必要なければ取る。
対話モードでやるときは,最後の ';' を付けておく方がいいかもしれない。
R の data.table::fread() では 5.027 sec. であったので,ちょっと負けるなあ。
でも,Python でも 28.793 sec. なので,よしとしよう。
julia> row, col = size(df) # データフレームのサイズ
(100000, 1500)
データフレームの最初の方の確認
julia> first(df, 5)
5×1500 DataFrame
Row │ X1 X2 X3 X4 ⋯
│ Float64 Float64 Float64 Float64
────┼──────────────────────────────────────
1 │ 51.26 44.35 38.61 36.61
2 │ 41.03 59.43 48.48 59.44
3 │ 61.89 29.32 64.51 51.07
4 │ 56.88 59.77 49.92 48.76
5 │ 69.43 56.75 65.3 47.28 ⋯
1488 columns omitted
データフレームの最後の方の確認
julia> last(df, 5)
5×1500 DataFrame
Row │ X1 X2 X3 X4 ⋯
│ Float64 Float64 Float64 Float64
────┼──────────────────────────────────────
1 │ 48.05 58.57 44.79 56.38
2 │ 79.41 41.44 53.72 52.31
3 │ 61.82 48.27 60.91 36.46
4 │ 49.19 24.26 49.97 44.7
5 │ 51.66 66.37 56.99 55.78 ⋯
1488 columns omitted
1 列目(変数名: "X1") の指定法
julia> sum(df[!, 1]) # 列番号で指定
5.004236609999999e6
julia> sum(df[!, "X1"]) # 変数名で指定 その1 df[!, 1],df[!, :1] も同じ
5.004236609999999e6
julia> sum(df.X1) # 変数名で指定 その2 df.X1 でも同じ
5.004236609999999e6
df[!, [:X1]] と df[:, [:X1]] はデータフレームだが,df[!, :X1] と df[:, :X1] はベクトル
df[!, "X1"] はコピーを作らない,df[:, "X1"] はコピーを作る
julia> df[!, "X1"] === df[:, "X1"] # === は同一かどうか(メモリー上で同じ位置にあるもの)
false
julia> df[!, "X1"] == df[:, "X1"] # == は等しいかどうか
true
julia> df[:, [:X2, :X5]]
100000×2 DataFrame
Row │ X2 X5
│ Float64 Float64
────────┼──────────────────
1 │ 44.35 54.22
2 │ 59.43 44.9
3 │ 29.32 34.25
4 │ 59.77 43.93
以上の他にも何種類かある。
行の抽出
julia> df2 = df[15:36, :]
22×1500 DataFrame
Row │ X1 X2 X3 ⋯
│ Float64 Float64 Float64 ⋯
────┼───────────────────────────────
1 │ 58.78 39.62 72.1 ⋯
2 │ 46.84 59.54 46.05 ⋯
:
22 │ 69.09 54.01 54.76
julia> size(df2)
(22, 1500)
抽出と同時に並べ替えもできる。
julia> df3 = df[[5, 2, 7], :]
3×1500 DataFrame
Row │ X1 X2 X3
│ Float64 Float64 Float64
────┼───────────────────────────
1 │ 69.43 56.75 65.3 ⋯
2 │ 41.03 59.43 48.48
3 │ 44.68 59.1 51.65
julia> size(df3)
(3, 1500)
列の抽出
julia> df4 = df[:, ["X1", "X5", "X2"]]
100000×3 DataFrame
Row │ X1 X5 X2
│ Float64 Float64 Float64
────────┼───────────────────────────
1 │ 51.26 54.22 44.35
2 │ 41.03 44.9 59.43
3 │ 61.89 34.25 29.32
4 │ 56.88 43.93 59.77
:
julia> size(df4)
(100000, 3)
行と列を同時に抽出
上の応用。
julia> df5 = df[[10, 5, 3], ["X1", "X5", "X2"]]
3×3 DataFrame
Row │ X1 X5 X2
│ Float64 Float64 Float64
─────┼───────────────────────────
1 │ 49.09 56.05 45.22
2 │ 69.43 45.76 56.75
3 │ 61.89 34.25 29.32
julia> size(df5)
(3, 3)
条件を満たす行の抽出
julia> df6 = df[df.X1 .> 87, ["X2", "X6", "X9"]] # > 前のピリオドを忘れないように
9×3 DataFrame
Row │ X2 X6 X9
│ Float64 Float64 Float64
─────┼───────────────────────────
1 │ 55.27 59.61 64.16
2 │ 38.27 38.72 41.42
3 │ 38.24 53.88 29.97
該当セルへの代入
行と列の指定法がわかれば,該当セルへの代入も同じように行えることがわかる。
julia> df7[1, 2] = 99999
99999
julia> df7
4×4 DataFrame
Row │ X6 X4 X1 X2
│ Float64 Float64 Float64 Float64
─────┼───────────────────────────────────
1 │ 38.72 99999.0 90.19 38.27
2 │ 49.75 49.8 89.25 64.74
3 │ 70.82 24.25 89.77 42.46
4 │ 34.49 54.26 92.58 55.82
列全部を代入対象とすることもできる。'.=' に注意。
julia> df7[!, 1] .= 77777
4-element Array{Int64,1}:
77777
77777
77777
77777
julia> df7
4×4 DataFrame
Row │ X6 X4 X1 X2
│ Int64 Float64 Float64 Float64
─────┼───────────────────────────────────
1 │ 77777 99999.0 90.19 38.27
2 │ 77777 49.8 89.25 64.74
3 │ 77777 24.25 89.77 42.46
4 │ 77777 54.26 92.58 55.82
並べ替え(ソート)
列を基準としてソートする。
julia> df8 = CSV.sort(df7, :X1)
4×4 DataFrame
Row │ X6 X4 X1 X2
│ Int64 Float64 Float64 Float64
─────┼───────────────────────────────────
1 │ 77777 49.8 89.25 64.74
2 │ 77777 24.25 89.77 42.46
3 │ 77777 99999.0 90.19 38.27
4 │ 77777 54.26 92.58 55.82
Julia のベンチマークテスト:@times と BenchmarkTools の @benchmark
まだ BenchmarkTools をインストールしていないなら,まずはパッケージのインストール。
(@v1.5) pkg> add BenchmarkTools
Updating registry at `~/.julia/registries/General`
######################################################################## 100.0%
Resolving package versions...
Installed BenchmarkTools ─ v0.5.0
Updating `~/.julia/environments/v1.5/Project.toml`
[6e4b80f9] + BenchmarkTools v0.5.0
Updating `~/.julia/environments/v1.5/Manifest.toml`
[6e4b80f9] + BenchmarkTools v0.5.0
ベンチマークは,関数を対象にする。
2つの関数,f1, f2 を定義する。いずれも 3 つの引数の和をとるものだが,鶏を割くのに牛刀を用いるような sum([x, y, z]) と 単に x + y + z の足し算をする方法の比較。
julia> f1(x, y, z) = sum([x, y, z])
f1 (generic function with 1 method)
julia> f2(x, y, z) = x + y + z
f2 (generic function with 1 method)
@benchmark を使うときには一度だけ using が必要。
julia> using BenchmarkTools
[ Info: Precompiling BenchmarkTools [6e4b80f9-dd63-53aa-95a3-0cdb28fa8baf]
実行する関数の前に @benchmark を付けるだけ。
julia> @benchmark f1(1, 2, 3)
BenchmarkTools.Trial:
memory estimate: 112 bytes
allocs estimate: 1
--------------
minimum time: 40.868 ns (0.00% GC)
median time: 43.567 ns (0.00% GC)
mean time: 47.606 ns (3.71% GC)
maximum time: 1.103 μs (95.23% GC)
--------------
samples: 10000
evals/sample: 991
julia> @benchmark f2(1, 2, 3)
BenchmarkTools.Trial:
memory estimate: 0 bytes
allocs estimate: 0
--------------
minimum time: 0.018 ns (0.00% GC)
median time: 0.032 ns (0.00% GC)
mean time: 0.028 ns (0.00% GC)
maximum time: 0.039 ns (0.00% GC)
--------------
samples: 10000
evals/sample: 1000
単に足し算する方が圧倒的に速い(まあ,ゴミのような差なので,比較する意味はないが)。
なお,何もしないで使える方法で @time を使うやり方もある。これは,関数を一度だけ実行した上でのの計測なので,振れ幅が大きい。
julia> @time f1(1, 2, 3)
0.000001 seconds (1 allocation: 112 bytes)
6
julia> @time f2(1, 2, 3)
0.000000 seconds
6
実行時間がかかるなあと思ったら,@benchmark してみるのがお勧めです。
さて,下請け関数をコンパイラ言語で書いたらどうなるかということで,私が一番とっつきやすい FORTRAN(雀百まで踊り忘れず)を使って,以下のようなプログラムを書いた。
function is_prime(x)
implicit none
integer(8) mx, x, i
logical is_prime
if (x == 2 .or. x == 3) then
is_prime = .true.
return
else if (x <= 1 .or. mod(x, 2) == 0 .or. mod(x, 3) == 0) then
is_prime = .false.
return
end if
mx = int(sqrt(float(x)))
do i = 5, mx, 6
if (mod(x, i) == 0) then
is_prime = (x == i)
return
else if (mod(x, i + 2) == 0) then
is_prime = (x == i + 2)
return
end if
end do
is_prime = .true.
end function is_prime
function next_prime(x)
implicit none
integer(8) x, i, next_prime
logical is_prime
x = x + 1
next_prime = 0
do i = x, 9223372036854775807_8 ! 巨大整定数の宣言 2^63 - 1
if (is_prime(i)) then
next_prime = i
return
end if
end do
end function next_prime
これを,
$ f2py -m prime_lib -c is_prime.f90
で
prime_lib.cpython-38-darwin.so
というシェアードライブラリを作る。
それを利用するには,まずインポートして
import prime_lib
prime_lib.next_prime() のようにする。
from time import time
start = time()
k = 9223372036854775782
print(f"next_prime({k}) = {prime_lib.next_prime(k)}")
print(time() - start)
実行結果は
next_prime(9223372036854775782) = 9223372036854775783
0.00039386 秒で答えが出る(小数点以下3桁の秒数なんてほぼゴミなので無視して良いレベル)。
Python で書いたプログラムでは 197.028 秒だったから,50万倍くらいの速度だ。
Julia で書いたプログラムでは 9.343 秒だったから,2万4千倍くらいの速度だ。
Julia は大健闘しているものの,やはりコンパイラ言語には太刀打ちできない。
さて,前の記事で Python による素数判定プログラムを評価したが,今回は Python プログラムを Julia に移植した結果を書く。
まず,2 を特別にして,あとは奇数で試し割りをするプログラムである。
Julia は色々な変数タイプが使えるが,符号付き 64 ビット整数の Int64 を使うことにする。
使用法は,x::Int64 のように変数のアノテーションを行う(初出の一回だけでよいようだ)。
他の型からの変更は Int64() のように行う。
function is_prime0(x::Int64)
if x == 2
return true
elseif x <= 1 || x % 2 == 0
return false
end
mx::Int64 = Int64(floor(sqrt(x)))
for i::Int64 in 3:2:mx
if x % i == 0
return false
end
end
return true
end
2 と 3 を別扱いにして 6n ± 1 で試し割りを行うバージョンが以下のプログラム。
function is_prime(x::Int64)
if x == 2 || x == 3
return true
elseif x <= 1 || x % 2 == 0 || x % 3 == 0
return false
end
mx::Int64 = Int64(floor(sqrt(x)))
for i::Int64 in 5:6:mx
if x % i == 0
return x == i
elseif x % (i + 2) == 0
return x == i + 2
end
end
return true
end
これを利用して,与えた数より大きい最小の素数を返す関数を書く。
function next_prime(X::Int64)
X += 1
answer::Int64 = 0
for i::Int64 in X:9223372036854775783
if is_prime(i)
answer = i
break
end
end
return answer
end
実行時間の測定は 対象とする文の前に '@time' を付けるだけでよい。
@time println(next_prime(Int64(9223372036854775782))) # 9223372036854775783, 9.343510s
Python の場合
next_prime(9223372036854775782) は 197.028s だったので,ほぼ 20 倍速いということになった。
原作者が最初に書いた関数。
本人も認めるとおり,速度的には超マズイ。
def is_prime000(x: int) -> bool:
if x <= 1:
return False
for i in range(2, x):
if x % i == 0:
return False
return True
試し割りはその数の平方根までで十分。
そこまでの数で割りきれなければ,素数である。
import math
def is_prime00(x: int) -> bool:
if x <= 1:
return False
for i in range(2, (math.floor(math.sqrt(x)) + 1)):
if x % i == 0:
return False
return True
原作者はここまで努力はしたものの,もっと速い方法(コンパイラを使う)を探ることにしてしまった。
しかし,よいアルゴリズムを使わないと,コンパイラでもカバーしきれないのはよく知られていることだ。もう少しプログラムを改良しよう。
素数は 2 だけが偶数で,それ以外は奇数。
よって,2 を特別扱いし,その他の素数候補の試し割りを行うのは奇数だけ。ということを使ったのが次のプログラム。
def is_prime0(x: int) -> bool:
if x == 2:
return True
elif x <= 1 or x % 2 == 0:
return False
for i in range(3, int(x**0.5 + 1), 2):
if x % i == 0:
return False
return True
さらに改良を加えよう。
5 以上の素数は 6n ± 1 の形をしている。
従って,2,3 を特別扱いし,その他の素数候補の試し割りを行うのは 6n ± 1 だけ。
def is_prime(x: int) -> bool:
if x in [2, 3]:
return True
elif x <= 1 or x % 2 == 0 or x % 3 == 0:
return False
for i in range(5, int(x**0.5 + 7), 6):
if x % i == 0:
return x == i
elif x % (i + 2) == 0:
return x == i + 2
return True
さて,4 つのプログラムの速度を評価しよう。
1000000007 は素数であるが,is_prime000(), is_prime00(), is_prime0(), is_prime() の計算時間を比較すると,80 秒,0.003 秒,0.002 秒,0.001 秒程度である。しかし,is_prime000() 以外は,誤差の範囲内でしかない。
from time import time
start = time(); print(is_prime000(1000000007), time() - start) # True 80.07880806922913
start = time(); print(is_prime00(1000000007), time() - start) # True 0.0031898021697998047
start = time(); print(is_prime0(1000000007), time() - start) # True 0.001580953598022461
start = time(); print(is_prime(1000000007), time() - start) # True 0.001107931137084961
しかし,92233720368547841 が素数かどうかを判定するのは,is_prime() でも 15 秒かかる。
start = time(); print(is_prime(92233720368547841), time() - start) # True 15.08924412727356
is_prime0() が 20 秒,is_prime00() が 40 秒ほどである。
start = time(); print(is_prime0(92233720368547841), time() - start) # True 20.365103244781494
start = time(); print(is_prime00(92233720368547841), time() - start) # True 40.88630700111389
上の 1000000007 の素数判定にかかる計算時間との関係から,もし is_prime000() で判定するとしたら 80:0.003 = x:40 つまり, x = 80/0.003 * 40 = 1066666.667 秒 = 12.3 日 かかる。
さて,素数判定プログラムができれば,一つの利用法は,与えられた数より大きい最小の素数を求めるプログラムを書くこと。
def next_prime(x):
x += 1
answer = 0
for i in range(x, 9223372036854775783 + 1):
if is_prime(i):
answer = i
break
return answer
start = time(); print(next_prime(10000000000000000), time() - start) # 10000000000000061, 7.773s
start = time(); print(next_prime(92233720368547757), time() - start) # 92233720368547841, 15.040s
大きな数を素数判定しようとすると,かなりの時間が掛かることになる。
start = time(); print(next_prime(9223372036854775782), time() - start) # 9223372036854775783, 197.028s
ここではじめてコンパイラ言語の使用を検討することにするが,その前に,Julia でプログラムしてみよう。
ツェラーの公式を利用して列挙する
def Zeller(y, m, d):
w = ['Sat', 'Sun', 'Mon', 'Tue', 'Wed', 'Thu', 'Fri']
if m == 1 or m ==2:
m += 12
y -= 1
C = y // 100
Y = y % 100
return w[(d + 26*(m+1)//10 + Y + Y//4 -2*C + C // 4) % 7]
for y in range(2021, 2030):
for m in range(1, 13):
if Zeller(y, m, 13) == 'Fri':
print(y, m)
2021 8
2022 5
2023 1
2023 10
2024 9
2024 12
2025 6
2026 2
2026 3
2026 11
2027 8
2028 10
2029 4
2029 7
データフレームのマークダウン出力ができるようになった
>>> pd.__version__
'1.0.1'
>>> df = pd.DataFrame({"a": list("abcde"), "b": [1,2,3,4,5]})
>>> df
a b
0 a 1
1 b 2
2 c 3
3 d 4
4 e 5
>>> df.to_markdown()
'| | a | b |\n|---:|:----|----:|\n| 0 | a | 1 |\n| 1 | b | 2 |\n| 2 | c | 3 |\n| 3 | d | 4 |\n| 4 | e | 5 |'
>>> print(df.to_markdown())
| | a | b |
|---:|:----|----:|
| 0 | a | 1 |
| 1 | b | 2 |
| 2 | c | 3 |
| 3 | d | 4 |
| 4 | e | 5 |
macOS Big SurでPythonをはじめてみる
という記事があったのだけど
- Pythonのバージョン2系とバージョン3系の解説があること
- バージョン3へのアップグレードについて記述があること
- プログラム経験はあるけど、Pythonは初心者という人向けであること
とはいっているものの,不安だなあ。
Mac OS は,いまだに Python 2 を推奨しているということか?
推奨していなくても,受け取る側は「推奨されている」とオモウワナア!
大丈夫か?
もうねえ,Python 3.9 にすべき,というか。
もう,初めからやるなら,Julia がお勧め。
もうねえ,いまどき,Python やってる場合じゃない,と,思いますよ。
一歩先を行きませんか????
みんなと同じことやってる場合じゃない。



















