算額（その1619）

算額（その1619）

福島県 福島郷社稲荷社 明治22年(1889)
～落書き帳「○△□」～ 600. 第９回【街角の問題】
http://streetwasan.web.fc2.com/math19.5.30.html
キーワード：円4個，正方形，対角線，斜線2本
#Julia, #SymPy, #算額, #和算, #数学

正方形の中に対角線（方斜）1 本，斜線 2 本を引き，区画された領域に等円 4 個を容れる。対角線の長さが 54.56 寸のとき，等円の直径はいかほどか。

ページの作者は，『原文では何故「方斜」を、それも「五十四寸五分六厘」という中途半端な数値で与えているのか。解いてみれば分からなくもありませんが、ここでは不問としておきましょう。』と言っている。

ここでは普通に（？），方斜ではなく正方形の一辺（方面）を与えて等円の直径を求めることにする（方斜が与えられたらそれを 1/√2 倍して，計算すればよい）。

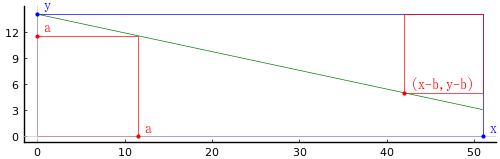
正方形の一辺の長さを a
等円の半径と中心座標を r, (r, y), (x, r), (a- y, a - r), (a - r, a - x)
とおき，以下の連立方程式を解く。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy
@syms a::positive, b::positive, r::positive, x::positive, y::positive

eq1 = dist2(0, a, b, 0, r, y, r)/b
eq2 = dist2(0, a, b, 0, x, r, r)/a
eq3 = dist2(0, 0, a, a, r, y, r)*2
eq4 = dist2(0, a, a, 0, x, r, r)*2
res = solve([eq1, eq2, eq3, eq4], (r, b, x, y))[4]  # 4 of 5

    (-a*sqrt(-1 + 2*sqrt(2))/2 + sqrt(2)*a/4 + sqrt(2)*a*sqrt(-1 + 2*sqrt(2))/4, a*(-sqrt(-1 + 2*sqrt(2)) + 1 + sqrt(2))/2, a*(-6*sqrt(-1 + 2*sqrt(2)) - 3*sqrt(2) + 4 + 5*sqrt(-2 + 4*sqrt(2)))/(2*(-3*sqrt(2) - 2*sqrt(-1 + 2*sqrt(2)) + sqrt(2)*sqrt(-1 + 2*sqrt(2)) + 6)), a*(-sqrt(-1/2 + sqrt(2))/2 + sqrt(2)/4 + 1/2))

# r
res[1] |> factor

SymPy ではこれ以上簡約化できないが，紙と鉛筆で
a*(sqrt(2√2 - 1)*(√2 - 2) + √2)/4
になる。

方斜が 54.56 寸のとき正方形の一辺の長さは a = 54.56/√2 なので，等円の半径は 6.000278751635302，直径は 12.000557503270604 である。

(54.56/√2)*(sqrt(2√2 - 1)*(√2 - 2) + √2)/4

    6.000278751635302

方斜が 54.56 のとき，等円の直径は 12.0005575032706 である。
このとき正方形の一辺の長さは 38.579745981538 で，方斜よりもっときれいな数ではない。

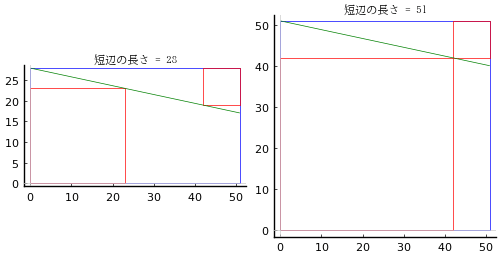
正方形の一辺の長さが 21115（整数）のとき，等円の直径は 6568.00000193929 である。小数点のあと 5 個も 0 が続く。
しかしこのときの方斜は 29861.1193695079 で，きれいな数ではない。

function draw(a, more=false)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
    (r, b, x, y) = (-a*sqrt(-1 + 2*sqrt(2))/2 + sqrt(2)*a/4 + sqrt(2)*a*sqrt(-1 + 2*sqrt(2))/4, a*(-sqrt(-1 + 2*sqrt(2)) + 1 + sqrt(2))/2, a*(-6*sqrt(-1 + 2*sqrt(2)) - 3*sqrt(2) + 4 + 5*sqrt(-2 + 4*sqrt(2)))/(2*(-3*sqrt(2) - 2*sqrt(-1 + 2*sqrt(2)) + sqrt(2)*sqrt(-1 + 2*sqrt(2)) + 6)), a*(-sqrt(-1/2 + sqrt(2))/2 + sqrt(2)/4 + 1/2))
    方斜 = √2a
    @printf("方斜 %.15g のとき，等円の直径は %.15g である。\n", 方斜, 2r)
    @printf("a = %.15g;   b = %g;   r = %g;   x = %g;   y = %g\n", a, b, r, x, y)
    plot([0, a, a, 0, 0], [0, 0, a, a, 0], color=:green, lw=0.5)
    circle(r, y, r)
    circle(a- y, a - r, r)
    circle(x, r, r)
    circle(a - r, a - x, r)
    segment(0, 0, a, a, :blue)
    segment(0, a, b, 0, :blue)
    segment(0, a, a, a - b, :blue)
    if more
        delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
        hline!([0], color=:gray80, lw=0.5)
        vline!([0], color=:gray80, lw=0.5)
        point(a, a, "(a,a)", :green, :right, :bottom, delta=delta/2)
        point(b, 0, "(b,0)  ", :green, :right, :bottom, delta=delta/2)
        point(r, y, "等円:r,(r,y)", :red, :center, delta=-delta/2)
        point(x, r, "等円:r,(x,r)", :red, :center, delta=-delta/2)
    end
end;

#draw(54.56/√2, true)
draw(21115, true)

算額（その1618）

算額（その1618）

福島県白河市南湖 南湖神社 昭和58年(1983)
http://www.wasan.jp/fukusima/nanko.html
キーワード：円5個，外円，楕円，面積
#Julia, #SymPy, #算額, #和算, #数学

外円の中に楕円 1 個と等円 4 個を容れる。等円の面積が与えられたとき，赤積を求めよ。

外円の半径と中心座標を R, (0, 0)
等円の半径と中心座標を r, (R - r, 0), (0, R - r)
楕円の長半径，短半径と中心座標を a, b, (0, 0)
とおく。

a = R, b = R - 2r である。
また，楕円内の等円は曲率円なので，r = b^2/a である。

等円の面積 = π*r^2
赤積 = 外円の面積 - 楕円の面積 - 2×等円の面積
    = π*R^2 - π*a*b - 2π*r^2

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy
@syms R, r, a, b
a = R
b = R - 2r
eq = r - (R - 2r)^2/R  # b^2/a
ans_r = solve(eq, r)[1]
ans_r |> println

    R/4

等円の半径は外円の半径の 1/4 である。

等円の面積 = (PI*r^2)(r => R/4)
等円の面積 |> println

    pi*R^2/16

赤積 = (PI*R^2 - PI*a*b - 2PI*r^2)(r => R/4)
赤積 |> println

    3*pi*R^2/8

赤積と等円の面積の比を取ると 6 である。
赤積は，等円の面積の 6 倍である。

赤積/等円の面積 |> println

    6

function draw(R, more=false)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
    r = R/4
    a = R
    b = R - 2r
    plot()
    circlef(0, 0, R)
    ellipse(0, 0, a, b, color=:orange, fcolor=:orange)
    circle42f(0, R - r, r, :black)
    if more
        delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
        hline!([0], color=:gray80, lw=0.5)
        vline!([0], color=:gray80, lw=0.5)
    end
end;

draw(1, true)

算額（その1617）

算額（その1617）

山形県鶴岡市大山 椙尾神社 文政元年8月
http://www.wasan.jp/yamagata/sugio.html
キーワード：円2個，円弧，直角三角形
#Julia, #SymPy, #算額, #和算, #数学

外円の一部の円弧（弓形）の中に楕円を容れる。楕円の長径が 6 寸，短径が 3 寸，矢が 3.1 寸のとき外円の直径はいかほどか。

外円の半径と中心座標を R, (0, 0)
楕円の半径と中心座標を a, b, (0, R - 矢 + b)
円弧と楕円の接点座標を (x0, y0)
とおき，以下の連立方程式を解く。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy
@syms R::positive, x0::positive, y0::positive, a::positive, b::positive, 矢::positive
eq1 = x0^2/a^2 + (y0 - (R - 矢 + b))^2/b^2 - 1
eq2 = x0^2 + y0^2 - R^2
eq3 = -b^2*x0/(a^2*(y0 - (R - 矢 + b))) + x0/y0;
res = solve([eq2, eq3], (x0, y0))[2];

# x0
@syms d
ans_x0 = res[1] |> simplify |> x -> apart(x, d) |> simplify
ans_x0 |> println

    sqrt(-2*R^2*a^2*b^2 + R^2*b^4 - 2*R*a^4*b + 2*R*a^4*矢 - a^4*b^2 + 2*a^4*b*矢 - a^4*矢^2)/(a^2 - b^2)

# y0
ans_y0 = res[2]
ans_y0 |> println

    a^2*(R + b - 矢)/(a^2 - b^2)

eq11 = eq1(x0 => ans_x0, y0 => ans_y0) |> simplify |> numerator;

# R
ans_R = solve(eq11, R)[1]  # 1 of 2
ans_R |> println

    a*(a*(-b + 矢) - sqrt(矢)*sqrt(-2*a^2*b + a^2*矢 + 2*b^3 - b^2*矢))/b^2

長径が 6，短径が 3，矢が 3.1 のとき，外円の直径は 8.94254 である。

2ans_R(a => 6/2, b => 3/2, 矢 => 3.1).evalf() |> println

    8.94253969560281

function draw(a, b, 矢, more=false)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
    R = a*(a*(-b + 矢) - sqrt(矢)*sqrt(-2*a^2*b + a^2*矢 + 2*b^3 - b^2*矢))/b^2
    x0 =  sqrt(-(R*b^2 + a^2*b - a^2*矢)*(2*R*a^2 - R*b^2 + a^2*b - a^2*矢))/((a - b)*(a + b))
    y0 = a^2*(R + b - 矢)/(a^2 - b^2)
    y = R - 矢
    x = sqrt(R^2 - y^2)
    θ = atand(y, x)
    @printf("長径が %g，短径が %g，矢が %g のとき，外円の直径は %g である。\n", 2a, 2b, 矢, 2R)
    @printf("x0 = %g;  y0 = %g\n", x0, y0)
    plot()
    circle(0, 0, R, :blue, beginangle=θ, endangle=180-θ, n=1000)
    ellipse(0, R - 矢 + b, a, b, color=:red)
    segment(-x, y, x, y, :blue)
    if more
        delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
        hline!([0], color=:gray80, lw=0.5)
        vline!([0], color=:gray80, lw=0.5)
        dimension_line(0, R, 0, y, "矢 ", :blue, :right, dx=-3delta)
        dimension_line(0, y + b, 0, y + 2b, " b", :red, :left)
        dimension_line(0, y + b, a, y + b, " a", :red, :center, delta=-2delta)
        point(0, R, "R", :blue, :center, :bottom, delta=2delta)
        point(0, y, "R-矢+b", :red, :center, delta=-2delta)
        point(x0, y0, "(x0,y0)", :red, :left, :bottom)
        point(0, y + b, "", :red)
        point(a, y + b, "", :red)
        point(0, y + 2b, "", :red)
    end
end;

draw(6/2, 3/2, 3.1, true)

算額（その1616）

算額（その1616）

山形県新庄市堀端町 戸澤神社（戸沢神社） 文政元年(1818)　
http://www.wasan.jp/yamagata/tozawa.html
キーワード：円2個，円弧，直角三角形
#Julia, #SymPy, #算額, #和算, #数学

直角三角形の中に，円弧，大円，小円を容れる。鈎，股が与えられたとき，小円の最小値を求めよ。

鈎，股をそのまま変数名とし，弦を前もって求めておく。
大円の半径と中心座標を r1, (r1, r1)
小円の半径と中心座標を r2, (r1 + 2sqrt(r1*r2), r2)
円弧の半径と中心座標を R, (x, y)
とおき，以下の連立方程式を立てる。

算額の図では，円弧は股に一点で交差または外接している。そのためには円弧の中心の x 座標が股の長さに等しくなければならない。もしその条件が満たされないと，円弧は股と 2 点で交差することになり，算額の図のようにはならない。つまり，円弧は股に接しているのである。そのとき小円は確定し，必然的に最小値になる。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy
@syms R::positive, x::positive, y::positive, r1::positive, r2::positive, 鈎::positive, 股::positive
@syms R, x, y, r1, r2, 鈎, 股
x = 股
y = R
eq1 = (x - r1)^2 + (y - r1)^2 - (R + r1)^2
eq2 = (x - (r1 + 2sqrt(r1*r2)))^2 + (y - r2)^2 - (R + r2)^2
eq3 = x^2 + (y - 鈎)^2 - R^2;

eq3 から円弧の半径，eq1 から大円の半径，eq2 から小円の半径が順次決定できる。

# R
ans_R = solve(eq3, R)[1]
ans_R |> println

    (股^2 + 鈎^2)/(2*鈎)

# r1
ans_r1 = solve(eq1, r1)[1]
ans_r1 |> println

    2*R + 股 - 2*sqrt(R*(R + 股))

# r2
@syms d
ans_r2 = solve(eq2, r2)[1] |> x -> apart(x, d) |> factor
ans_r2 |> println

    (r1 - 股)^2*(R + r1 - 2*sqrt(R*r1))/(4*(-R + r1)^2)

たとえば，鈎 = 3, 股 = 4　のとき，弦 = 5, r1 = 0.666666666666667 = 2/3, r2 = 0.340136054421768 である。

ans_r2(R => ans_R, r1 => 0.666666666666667)(鈎 => 3, 股 => 4).evalf() |>  println

    0.340136054421769

function draw(鈎, 股, more=false)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
    R = (股^2 + 鈎^2)/(2*鈎)
    x = 股
    y = R
    r1 = 2R + 股 - 2sqrt(R*(R + 股))
    r2 = (r1 - 股)^2*(R + r1 - 2sqrt(R*r1))/(4(r1 - R)^2)
    @printf("r1 = %g;  R = %g;  x = %g;  y = %g;  r2 = %g\n", r1, R, x, y, r2)
    plot([0, 股, 0, 0], [0, 0, 鈎, 0], color=:green, lw=0.5)
    circle(x, y, R, :magenta)
    circle(r1, r1, r1)
    circle(r1 + 2sqrt(r1*r2), r2, r2, :blue)
    if more
        delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
        hline!([0], color=:gray80, lw=0.5)
        vline!([0], color=:gray80, lw=0.5)
        point(x, y, "円弧:R,(x,y)", :magenta, :center, :bottom, delta=delta)
        point(x + 3delta, y - 7delta, "大円:r1,(r1,r1)", :red, :left, mark=false)
        point(x + 3delta, y - 10delta, "小円:r2,(r1+2√(r1*r2),r2)", :blue, :left, mark=false)
        segment(x, y, 股, 0, :orange)
    end
end;

draw(3, 4, true)

算額（その1615）

算額（その1615）

八戸市北糠塚　光龍寺 昭和54年(1979)8月18日 桑原秀夫 復元奉納
http://www.wasan.jp/aomori/koryuji.html
キーワード：正20面球
#Julia, #SymPy, #算額, #和算, #数学

直径が R の球の表面上に互いに等距離になるように 12 個の点を配置し，それらを結ぶと合同な曲面が 20 個できる。これを正 20 面球と呼ぶ。辺の長さはいかほどか。

球面上の 12 頂点は，この球に内接する一辺の長さが a の正 20 面体である。球の半径は R = (sqrt(10 + 2√5)/4)*a なので，a = R/(sqrt(10 + 2√5)/4) である。

正 20 面体の隣り合う頂点を A, B，重心を O としたとき，∠AOB = θ = 63.4349488229220° である。

using SymPy
@syms R, a, θ
eq1 = R - (sqrt(10 + 2√Sym(5))/4)*a
eq2 = 2R^2 - 2R^2*cos(θ) - a^2
res = solve([eq1, eq2], (θ, a))[2]

    (acos(sqrt(5)/5), 2*sqrt(2)*R/sqrt(sqrt(5) + 5))

θ = res[1]
θ |> println
deg = θ/PI*180
deg.evalf() |> println

    acos(sqrt(5)/5)
    63.4349488229220

A，B，O の3点を含む平面でこの外接球を切ると，切断面は半径 R の円になる。曲線ABはこの円の円周の θ/2π 倍である。

((θ/2PI) * (PI*2R)) |> println

    R*acos(sqrt(5)/5)

R = 6 のとき，正 20 面球の辺の長さは 6.64289230676454 である。

((θ/2PI) * (PI*2R))(R => 6).evalf() |> println

    6.64289230676454

 

算額（その1614）

算額（その1614）

八戸市北糠塚　光龍寺 昭和54年(1979)8月18日 桑原秀夫 復元奉納
http://www.wasan.jp/aomori/koryuji.html
キーワード：正12面球
#Julia, #SymPy, #算額, #和算, #数学

直径が R の球の表面上に互いに等距離になるように 20 個の点を配置し，それらを結ぶと合同な曲面が 12 個できる。これを正 12 面球と呼ぶ。辺の長さはいかほどか。

球面上の 20 頂点は，この球に内接する一辺の長さが a の正 12 面体である。球の半径は R = (√15 + √3)/4 * a なので，a = (√15 - √3)/3 * R である。

正 12 面体の隣り合う頂点を A, B，重心を O としたとき，∠AOB = θ = acos(√5/3) = 41.8103148957786° である。

using SymPy
@syms R, a, θ
eq1 = R - (sqrt(Sym(15)) + sqrt(Sym(3)))/4 * a
eq2 = 2R^2 - 2R^2*cos(θ) - a^2
res = solve([eq1, eq2], (θ, a))[2]

    (acos(sqrt(5)/3), -sqrt(3)*R/3 + sqrt(15)*R/3)

θ = res[1]
θ |> println
deg = θ/PI*180
deg.evalf() |> println

    acos(sqrt(5)/3)
    41.8103148957786

A，B，O の3点を含む平面でこの外接球を切ると，切断面は半径 R の円になる。曲線ABはこの円の円周の θ/2π 倍である。

((θ/2PI) * (PI*2R)) |> println

    R*acos(sqrt(5)/3)

R = 6 のとき，正 12 面球の辺の長さは 9.42477796076938 である。

((θ/2PI) * (PI*2R))(R => 6).evalf() |> println

    4.37836593736180

算額（その1613）

算額（その1613）

八戸市北糠塚　光龍寺 昭和54年(1979)8月18日 桑原秀夫 復元奉納
http://www.wasan.jp/aomori/koryuji.html
キーワード：正8面球
#Julia, #SymPy, #算額, #和算, #数学

直径が R の球の表面上に互いに等距離になるように 6 個の点を配置し，それらを結ぶと合同な曲面が 8 個できる。これを正 8 面球と呼ぶ。辺の長さはいかほどか。

球面上の 6 頂点は，この球に内接する一辺の長さが a の正 8 面体である。球の半径は R = a/√2 なので，a = √2R である。

正 8 面体の隣り合う頂点を A, B，重心を O としたとき，∠AOB = θ = 90° である。

using SymPy
@syms R, a, θ
eq1 = R - (√Sym(2)/2) * a
eq2 = 2R^2 - 2R^2*cos(θ) - (√Sym(2)R)^2
res = solve([eq1, eq2], (θ, a))[1]

    (pi/2, sqrt(2)*R)

θ = res[1]
θ |> println
deg = θ/PI*180
deg.evalf() |> println

    pi/2
    90.0000000000000

A，B，O の3点を含む平面でこの外接球を切ると，切断面は半径 R の円になる。曲線ABはこの円の円周の θ/2π 倍である。

((θ/2PI) * (PI*2R)) |> println

    pi*R/2

R = 6 のとき，正 8 面球の辺の長さは 9.42477796076938 である。

((θ/2PI) * (PI*2R))(R => 6).evalf() |> println

    9.42477796076938

 

算額（その1612）

算額（その1612）

八戸市北糠塚　光龍寺 昭和54年(1979)8月18日 桑原秀夫 復元奉納
http://www.wasan.jp/aomori/koryuji.html
キーワード：正6面球
#Julia, #SymPy, #算額, #和算, #数学

直径が R の球の表面上に互いに等距離になるように 8 個の点を配置し，それらを結ぶと合同な曲面が 6 個できる。これを正 6 面球と呼ぶ。辺の長さはいかほどか。

球面上の 8 頂点は，この球に内接する一辺の長さが a の正 6 面体である。球の半径は R = √(3a^2/4) なので，a = 2√3R/3 である。

正6面体の隣り合う頂点を A, B，重心を O としたとき，∠AOB = θ とおく。
三角形 AOB で OA, OB, ∠AOB で第二余弦定理を適用すると，θ = acosd(1/3) = 70.5287793655093 である。

using SymPy
@syms R, a, θ
eq1 = R - √Sym(3)*a
eq2 = 2R^2 - 2R^2*cos(θ) - (2√Sym(3)R/3)^2
res = solve([eq1, eq2], (θ, a))[2]

    (acos(1/3), sqrt(3)*R/3)

θ = res[1]
θ |> println
deg = θ/PI*180
deg.evalf() |> println

    acos(1/3)
    70.5287793655093

A，B，O の3点を含む平面でこの外接球を切ると，切断面は半径 R の円になる。曲線ABはこの円の円周の θ/2π 倍である。

((θ/2PI) * (PI*2R)) |> println

    R*acos(1/3)

R = 6 のとき，正6面球の辺の長さは 7.38575650404465 である。

((θ/2PI) * (PI*2R))(R => 6).evalf() |> println

    7.38575650404465

算額（その1611）

算額（その1611）

青森県八戸市北糠塚 光龍寺 昭和54年(1979)8月18日 桑原秀夫 復元奉納
http://www.wasan.jp/aomori/koryuji.html
キーワード：正4面球
#Julia, #SymPy, #算額, #和算, #数学

直径が R の球の表面上に互いに等距離になるように 4 個の点を配置し，それらを結ぶと合同な曲面が 4 個できる。これを正 4 面球と呼ぶ。辺の長さはいかほどか。

球面上の 4 頂点は，この球に内接する一辺の長さが a の正4面体である。
球の半径は R = a*(√6/4) なので，a = R*(2√6/4)である。

正4面体の隣り合う頂点を A, B，重心を O としたとき，∠AOB = θ とおく。
三角形 AOB で OA, OB, ∠AOB で第二余弦定理を適用すると，θ = acosd(-1/3) = 109.47122063449069 である。

using SymPy
@syms R, a, θ
eq1 = R - √Sym(6)*a/4
eq2 = 2R^2 - 2R^2*cos(θ) - a^2
res = solve([eq1, eq2], (θ, a))[2]

    (acos(-1/3), 2*sqrt(6)*R/3)

θ = res[1]
θ |> println
deg = θ/PI*180
deg.evalf() |> println

    acos(-1/3)
    109.471220634491

A，B，O の3点を含む平面でこの外接球を切ると，切断面は半径 R の円になる。曲線ABはこの円の円周の θ/2π 倍である。

((θ/2PI) * (PI*2R)) |> println

    R*acos(-1/3)

R = 6 のとき，正4面球の辺の長さは 11.4637994174941 である。

((θ/2PI) * (PI*2R))(R => 6).evalf() |> println

    11.4637994174941

算額（その1610）

算額（その1610）

福島県田村市船引町門鹿宮林 古室神社 明治16年(1883)頃
http://www.wasan.jp/fukusima/komuro.html
キーワード：直角三角形，正五角形
#Julia, #SymPy, #算額, #和算, #数学

長方形の中に大小の正方形を容れ，長方形の一つの頂点と大小の正方形の頂点を結ぶ斜線を引く。長方形の長辺が 51 寸，小正方形の一辺の長さが 9 寸のとき，長方形の短辺の長さはいかほどか。

大正方形，小正方形の一辺の長さを a, b
長方形の長辺，短辺の長さを x, y
とおき，以下の方程式を解く。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy
@syms a::positive, b::positive, x::positive, y::positive
eq1 = b/(x - b) - (y - a)/a
ans_y = solve(eq1, y)[1]
ans_y |> println

    a*x/(-b + x)

x = 51, b = 9 のとき，y = a*(17/14) である。
y, a の間には 17a = 14y の関係がある。
長方形の短辺の長さ y は，9 ≦ y ≦ 51 の範囲の任意の値を取れる。

しかし，問の最後に「乃各寸止」とある。整数解を求めよという意味であろう。
答は「横17寸」（現代で云う縦を横と称していた。横は長という）とある。
y, a の組としては，(17, 14) が最小解であるが，(34, 28), (51, 42) もありうる。

function draw(y, more=false)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
    (x, b) = (51, 9)
    a = y*(14/17)
    p = plot([0, x, x, 0, 0], [0, 0, y, y, 0], color=:blue, lw=0.5)
    rect(0, 0, a, a, :red)
    rect(x - b, y - b, x, y, :red)
    abline(0, y, -(y - a)/a, 0, x, :green)
        delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
        hline!([0], color=:gray80, lw=0.5)
        vline!([0], color=:gray80, lw=0.5)
    if more
        point(0, y, " y", :blue, :left, :bottom, delta=delta)
        point(0, a, " a", :red, :left, :bottom, delta=delta)
        point(x, 0, " x", :blue, :left, :bottom, delta=delta)
        point(x - b, y - b, " (x-b,y-b)", :red, :left, :bottom, delta=delta)
        point(a, 0, " a", :red, :left, :bottom, delta=delta)
        ylims!(-3delta, y + 5delta)
    end
    if !more
        point(51/2, y, @sprintf("短辺の長さ = %g", y), :black, :center, :bottom, delta=2delta, mark=false, fontsize=8)
    end
    return p
end;

draw(14, true)

算額（その1609）

算額（その1609）

福島県田村市船引町堀越明神前 明石神社(堀越明宮) 明治11年(1878)
http://www.wasan.jp/fukusima/horikosiakasi.html
キーワード：直角三角形，正五角形
#Julia, #SymPy, #算額, #和算, #数学

直角三角形の中に弦（斜辺）と股（底辺）を共有し，残りの頂点が鈎（高さ）上にある正五角形を容れる。
正五角形の一辺の長さが与えられたとき，股，鈎はいかほどか。

正五角形の一辺の長さを a, 正五角形を内接する円の半径を r とする。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy
@syms r::positive, 股::positive, a::positive
s36 = Sym(36)
s18 = s36/2
r = a/2sind(s36);

直角三角形の鈎は a*sqrt(sqrt(5)/8 + 5/8) + 2*a*sqrt(5/8 - sqrt(5)/8)，
正五角形の一辺の長さが 1 のとき，鈎 = 2.12662702088010 である。

鈎 = 2a*sind(s36) + a*cosd(s18)
鈎 |> println
鈎(a => 1).evalf() |> println

    a*sqrt(sqrt(5)/8 + 5/8) + 2*a*sqrt(5/8 - sqrt(5)/8)
    2.12662702088010

直角三角形と内部にある直角三角形の相似関係から，股を求める。

eq = 鈎/股 - (r + r*cosd(s36))/(股 - a/2 - a*sind(s18))
ans_股 = solve(eq, 股)[1];

股は √5 が二重根号の中にある複雑な式になり SymPy では自動では簡約化（有理化）できない。
正五角形の一辺の長さが 1 のとき，直角三角形の股（底辺）は 2.92705098312484 である。

ans_股 |> println
ans_股(a => 1).evalf() |> println

    sqrt(5)*a*(sqrt(sqrt(5) + 5) + 2*sqrt(5 - sqrt(5)))/(-3*sqrt(5)*sqrt(5 - sqrt(5)) - sqrt(5)*sqrt(sqrt(5) + 5) + 5*sqrt(5 - sqrt(5)) + 5*sqrt(sqrt(5) + 5))
    2.92705098312484

SymPy の手を借りながら（詳細省略），手動で有理化する。

num = ans_股 |> numerator
den = ans_股 |> denominator
d1 = den.args[1]
d2 = den.args[2]
d3 = den.args[3]
d4 = den.args[4]
den2 = den *(d1 + d2 + d3 + d4) |> expand |> simplify
num2 = num *(d1 + d2 + d3 + d4) |> expand |> simplify
ans_股2 = num2/den2 |> sympy.sqrtdenest |> simplify |> factor;

簡潔な式になった。
股 = a*(5 + 3√5)/4 で，正五角形の一辺の長さが 1 のとき，直角三角形の股（底辺）は 2.92705098312484 である。

ans_股2 |> println
ans_股2(a => 1).evalf() |> println

    a*(5 + 3*sqrt(5))/4
    2.92705098312484

function draw(a, more=false)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
    r = a/2sind(36)
    股 = sqrt(5)*a*(sqrt(sqrt(5) + 5) + 2*sqrt(5 - sqrt(5)))/(-3*sqrt(5)*sqrt(5 - sqrt(5)) - sqrt(5)*sqrt(sqrt(5) + 5) + 5*sqrt(5 - sqrt(5)) + 5*sqrt(sqrt(5) + 5))
    鈎 = 2a*sind(36) + a*cosd(18)
    println("股 = $股, 鈎 = $鈎")
    plot([0, 股, 0, 0], [0, 0, 鈎, 0], color=:blue, lw=0.5)
    plot!([0, a*sind(18), a*sind(18) + a, 2a*sind(18) + a, a*sind(18) + a/2, 0],
        [a*cosd(18), 0, 0, a*cosd(18), r + r*cosd(36), a*cosd(18)], color=:red, lw=0.5)
    if more
        delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
        hline!([0], color=:gray80, lw=0.5)
        vline!([0], color=:gray80, lw=0.5)
        point(a*sind(18), 0, "a*sind(18)", :red, :center, delta=-delta)
        point(a*sind(18) + a/2, 0, "a*sind(18)+a/2", :red, :left, delta=-delta, deltax=-3delta)
        point(股, 0, "股", :red, :center, delta=-delta)
        point(0, a*cosd(18), " a*cosd(18) ", :red, :left, :vcenter)
        point(0, 鈎, " 鈎=a*cosd(18) + 2rsind(36)", :red, :left, :vcenter)
        dimension_line(a*sind(18) + a/2, 0, a*sind(18) + a/2, r + r*cosd(36), " (a*sind(18)+a/2, r+r*cosd(36))", :blue, :center, :vcenter)
        segment(a*sind(18) + a/2, 0, a*sind(18) + a/2, r + r*cosd(36), :gray80)
        dimension_line(a*sind(18) + a/2, 0, 股, 0, " x=股-a*sind(18)-a/2", :blue, delta=2delta, dy=-5delta)
        ylims!(-8delta, 鈎 + 3delta)
    end
end;
draw(1, true)

算額（その1608）

算額（その1608）

福島県田村市船引町堀越明神前 明石神社(堀越明宮) 明治11年(1878)
http://www.wasan.jp/fukusima/horikosiakasi.html

～落書き帳「○△□」～  696. 第10回「街角の問題」―堀越村明宮神社算額（その３）
http://streetwasan.web.fc2.com/math19.9.27.html
キーワード：円7個，直線上
#Julia, #SymPy, #算額, #和算, #数学

直線上に，東円 1 個，西円 2 個，南円 1 個，北円 3 個を載せる。東円の直径が 5 寸のとき北円の直径はいかほどか。

注：horikosiakasi.html の写真では，「北円径一寸四分□東円径幾何」とあり，「答曰東円径五寸」となっている。

東円の半径と中心座標を r1, (0, 2r3 - r1)
西円の半径と中心座標を r2, (r2, r2)
南円の半径と中心座標を r3, (0, r3)
北円の半径と中心座標を r4, (x4, y4), (0, r4)
とおき，以下の連立方程式を解く。

まず，右にある西円と中央の 北円が外接する条件 eq4 で，r2 を求めると，r2 = 4r4 であることがわかる。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy
@syms r1::positive, r2::positive, r3::positive, r4::positive, x4::positive, y4::positive
eq4 = r2^2 + (r2 - r4)^2 - (r2 + r4)^2;
ans_r2 = solve(eq4, r2)[1]
ans_r2 |> println

    4*r4

r2 = 2r4 である。また，y4 = 2r4 でもある。
これを条件として加え，残りの 3 方程式を解く。

horikosiakasi.html の「北円径一寸四分□東円径幾何」に基づき（r4 が与えられたとき），r1, r3, x4 を求める。

r2 = 4r4
y4 = 2r4
eq1 = r2^2 + (2r3 - r1 - r2)^2 - (r1 + r2)^2 |> expand
eq2 = x4^2 + (r3 - y4)^2 - (r3 + r4)^2 |> expand
eq3 = (x4 - r2)^2 + (y4 - r2)^2 - (r4 - r2)^2 |> expand
res = solve([eq1, eq2, eq3], (r1, r3, x4))[2]  # 2 of 2

    (r4*(7*sqrt(5) + 27)/12, 4*r4*(sqrt(5) + 3)/3, r4*(sqrt(5) + 4))

# r1 東円
res[1] |> println

    r4*(7*sqrt(5) + 27)/12

東円の半径 r1 は，北円の半径 r4 の (7√5 + 27)/12 = 3.5543729868748777 倍である。
北円の直径が 1 寸 4 分のとき，東円の直径は 1.4*(7√5 + 27)/12 = 4.976122181624828 寸である。

「術」は「北径を 0.28 で割れ」とあり，1.4/0.28 = 5 である。
実にきれいな結果になるが，0.28 は，r4 に掛ける倍数とすれば 1/0.28 = 3.571428571428571 なので，(7√5 + 27)/12 = 3.5543729868748777 の近似値ではなく，答えが 5 になるように選んだものであろう。

ということで，ちょっと汚いので，「落書き帳」ではこれを逆にしたのであろう。

「連立方程式を解く」というメソッドを取っているので，方程式はそのままで，何を求めるかを変えればよいだけである。

r1 が与えられるとして，r3, r4, x4 を求めればよい。

res2 = solve([eq1, eq2, eq3], (r3, r4, x4))[2]  # 2 of 2

    (24*sqrt(5)*r1/121 + 184*r1/121, -21*sqrt(5)*r1/121 + 81*r1/121, 6*r1*(73/242 - sqrt(5)/242))

# r3
res[1] |> simplify |> println

    r4*(7*sqrt(5) + 27)/12

# r4
res[2] |> simplify |> println

    4*r4*(sqrt(5) + 3)/3

# x4
res[3] |> simplify |> println

    r4*(sqrt(5) + 4)

北円の半径 r4 は，東円の半径 r1 の 3(27 - 7√5)/121 である。
東円の直径が 5 寸のとき，北円の直径は 1.4067178707646453 寸である。

これならば，「小数点以下 1 桁まで取って，北円の直径は 1 寸 4 分である」としても，さほどの違和感はない。（しかし，算額の原文を変更するのはあまり好ましいものとは思えない）

5*3(27 - 7√5)/121

    1.4067178707646453

function draw(r1, more=false)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
    r3 = r1*8(3√5 + 23)/121
    r4 = r1*3(27 - 7√5)/121
    x4 = r1*3(73 - √5)/121
    r2 = 4r4
    y4 = 2r4
    @printf("r1 = %g;  r2 = %g;  r3 = %g;  r4 = %g;  x4 = %g;  y4 = %g\n", r1, r2, r3, r4, x4, y4)
    plot()
    circle(0, r3, r3)
    circle2(r2, r2, r2, :blue)
    circle(0, 2r3 - r1, r1, :green)
    circle2(x4, y4, r4, :magenta)
    circle(0, r4, r4, :magenta)
    if more
        delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
        hline!([0], color=:gray80, lw=0.5)
        vline!([0], color=:gray80, lw=0.5)
        hline!([r4, 2r4, 3r4, 4r4], color=:orange, lw=0.5, style=:dot)
        point(0, 2r3 - r1, "東円:r1,(0,2r3-r1)", :green, :center, delta=-delta/2)
        point(r2, r2, "西円:r2,(r2,r2)", :blue, :center, delta=-delta/2)
        point(0, r3, "南円:r3,(0,r3)", :red, :center, delta=-delta/2)
        point(x4, y4, "北円:r4,(x4,y4)", :magenta, :center, delta=-delta/2)
        point(0, r4, "北円:r4,(0,r3)", :magenta, :center, delta=-delta/2)
    end
end;

draw(5/2, true)

 

算額（その1607）

算額（その1607）

宮城県石巻市尾崎宮下 久須師神社 明治20年(1887)
徳竹亜紀子，谷垣美保：2021年度の算額調査，仙台高等専門学校名取キャンパス研究紀要，第 58 号（2022），p.7-28.
https://www.sendai-nct.ac.jp/natori-library/wp-content/uploads/2022/03/kiyo2022-2.pdf
キーワード：円2個，円弧2個，斜線
#Julia, #SymPy, #算額, #和算, #数学

交差する円弧の中に等円を 2 個と共通接線を入れる。短径，長径，等円の直径が与えられたとき，共通接線と円弧の交点間の距離（斜の長さ）を求める術を述べよ。

等円の半径を r
円弧を構成する円の半径と中心座標を R, (0, 0)
等円の半径と中心座標を r, (x, y)
共通接線と円弧の交点座標を (x0, y0)
短径を 2K1, 長径を 2K2
とおく。

AB= K1 = R - y
BC = K2 = sqrt(R^2 - y^2) である。
以下の連立方程式を解き，(x0, y0, y, x, R) を求める。
これらは，K1, K2 を含む式で表される。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy
@syms R::positive, x::positive,
      y::positive, r::positive,
      x0::positive, y0::positive,
      K1::positive, K2::positive
eq1 = x^2 + y^2 - (R - r)^2
eq2 = r/x - (y0 - y)/sqrt(x0^2 + (y0 - y)^2)
eq3 = x0^2 + y0^2 - R^2
eq4 = (R - y) - K1
eq5 = sqrt(R^2 - y^2) - K2
res = solve([eq1, eq2, eq3, eq4, eq5], (x0, y0, y, x, R))[4]

    (K2^2*sqrt(-1/(K1*r - K2^2))*sqrt((K1^2*r - K1*K2^2 + K2^2*r)/(K1*r - K2^2))/sqrt(K1), (-K1^3*r + K1^2*K2^2 - K1*K2^2*r - K2^4)/(2*K1*(K1*r - K2^2)), (-K1^2 + K2^2)/(2*K1), sqrt(-(K1 - r)*(K1*r - K2^2))/sqrt(K1), (K1^2 + K2^2)/(2*K1))

斜の長さは 2sqrt(x0^2 + (y0 - y)^2) である。

# x0^2
x2 = res[1]^2 |> simplify
x2 |> println

    K2^4*(-K1^2*r + K1*K2^2 - K2^2*r)/(K1*(K1*r - K2^2)^2)

# (y0 - y)^2
y2 = (res[2] - res[3])^2 |> simplify
y2 |> println

    K2^4*r^2/(K1^2*r^2 - 2*K1*K2^2*r + K2^4)

# 斜 = 2sqrt(x0^2 + (y0 - y)^2) 
斜 = x2 + y2 |> simplify |> x -> sqrt(x) |> simplify |> x -> 2x

斜(K1 => 8/2, K2 => 16/2, r => 5/2) |> println

    10.6666666666667

徳竹も方法（経路）は違うが，結果として同じ式を導いている。

# 短径，長径，等円径はそれぞれの 1/2 で指定する
@syms 短径, 長径, 等円径
徳竹 = 長径^2*sqrt((短径 - 等円径)/(短径*(長径^2 - 短径*等円径)))

2*徳竹(短径 => 8/2, 長径 => 16/2, 等円径 => 5/2)|> println

    10.6666666666667

function draw(K1, K2, r, more=false)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
    (x0, y0, y, x, R) = (K2^2*sqrt(-1/(K1*r - K2^2))*sqrt((K1^2*r - K1*K2^2 + K2^2*r)/(K1*r - K2^2))/sqrt(K1), (-K1^3*r + K1^2*K2^2 - K1*K2^2*r - K2^4)/(2*K1*(K1*r - K2^2)), (-K1^2 + K2^2)/(2*K1), sqrt(-(K1 - r)*(K1*r - K2^2))/sqrt(K1), (K1^2 + K2^2)/(2*K1))
    斜 = sqrt(x0^2 + (y0 - y)^2)
    @printf("短径 = %g，長径 = %g，等円径 = %g のとき，斜の長さ = %g\n", 2K1, 2K2, 2r, 2斜)
    plot()
    θ = atand(y/sqrt(R^2 - y^2))
    circle(0, 0, R, beginangle=θ, endangle=180-θ, n=1000)
    circle(0, 2y, R, beginangle=180+θ, endangle=360-θ, n=1000)
    circle(x, y, r, :green)
    circle(-x, y, r, :green)
    segment(-x0, y - (y0 - y), x0, y0, :blue)
    if more
        delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
        hline!([0], color=:gray80, lw=0.5)
        vline!([0], color=:gray80, lw=0.5)
        point(x, y, "等円:r,(x,y)", :green, :center, delta=-delta)
        point(0, R, "R", :red, :center, :bottom, delta=delta)
        point(0, y, " y", :blue, :left, :vcenter)
        point(x0, y0, "(x0,y0)", :blue, :left, :bottom, delta=delta)
        dimension_line(0, y, sqrt(R^2 - y^2), y, "K2", :magenta, :center, :bottom, delta=2delta)
        dimension_line(0, R, 0, y, "K1 ", :orange, :right, :vcenter)
    end
end;

draw(8/2, 16/2, 5/2, true)png)

 

 

算額（その616）改訂版

算額（その616）改訂版

より鮮明な写真により，大円の中の小円は互いに外接しているのではないようなので，算額（その616）の改訂版を書く。

福島県白河市明神 境明神 万延元年(1860)
http://www.wasan.jp/fukusima/sakai1L2.html
拡大図
http://www.wasan.jp/fukusima/sakai1-2.png

団扇の中に小円 1 個と長方形が内接し，長方形の中に大円 2 個，小円 7 個が入っている。
小円の径を 1 としたとき，団扇の径はいかほどか。

団扇（外円）の半径と中心座標を R, (R0, 0); R0 < 0
大円の半径と中心座標を r2, (r2 - r, 0), (r - r2, 0)
小円の半径と中心座標を r，(x, r2 - r), (2r2 - 2r, 0), (0, 0)
長方形の右上の頂点座標は (2r2 - r, r2) である。

include("julia-source.txt")
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy
@syms r::positive, x::positive, r2::positive
eq1 = (x + r2 - r)^2 + (r2 - r)^2 - (r2 + r)^2
eq2 = (2r2 - 2r - x)^2 + (r2 - r)^2 - 4r^2
res = solve([eq1, eq2], (r2, x))[3]

    (-(-700*r^3*(8*sqrt(6)/25 + 22/25) - 58*r^3*(8*sqrt(6)/25 + 22/25)^2 + 40*r^3 + 175*r^3*(8*sqrt(6)/25 + 22/25)^3)/(192*r^2), r*(8*sqrt(6)/25 + 22/25))

# r2
ans_r2 = res[1] |> simplify
ans_r2 |> println

    3*r*(4*sqrt(6) + 11)/25

# x
ans_x = res[2] |> factor
ans_x |> println

    2*r*(4*sqrt(6) + 11)/25

外円の半径は (r2 + 2r - R0) で長方形の頂点を通ることから，中心座標（y 座標） R0 < 0 を求める。

@syms R0
eq3 = (2r2 - r)^2 + (r2 - R0)^2 - (r2 + 2r - R0)^2;
ans_R0 = solve(eq3, R0)[1];

# R0
ans_R0 |> println

    3*r/4 + 2*r2 - r2^2/r

# R0  r だけを含む式
ans_R0 = ans_R0(r2 => ans_r2) |> simplify
ans_R0 |> println

    3*r*(221 - 256*sqrt(6))/2500

# R
R = ans_r2 + 2r - ans_R0 |> simplify
R |> println

    r*(1968*sqrt(6) + 7637)/2500

R(r => 1/2).evalf() |> println
2*R(r => 1/2).evalf() |> println

    2.49151916275946
    4.98303832551892

小円の直径が 1 寸のとき，外円の直径は 4.98303832551892 寸である。

答は「答曰団扇径五寸」，術は「術曰置小径五之得団扇径合問」と術とは言えないものである。

この算額は問題の順番が答えになるように作られているので，4.98303832551892 の概数を答えにしたものであろうか。

function draw(r, more=false)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
    r2 = 3r*(4√6 + 11)/25
    x2 = 2r2/3
    println("r2 = $r2")
    R0 = 3r/4 + 2r2 - r2^2/r
    R = r2 + 2r - R0
    println("外円の直径は $(2R) である。")
    a = 2r2 - r
    b = r2
    plot([a, a, -a, -a, a], [-b, b, b, -b, -b], color=:green, lw=0.5)
    circle(0, R0, R, :magenta)
    circle2(r2 - r, 0, r2, :blue)
    circle4(x2, r2 - r, r)
    circle2(2r2 - 2r,  0, r)
    circle(0, 0, r)
    circle(0, r2 + r, r)
    if more
        delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
        vline!([0], color=:gray80, lw=0.5)
        hline!([0], color=:gray80, lw=0.5)
        point(0, R0, "R0")
        point(a, b, "(2r2-r,r2)", :green, :left, :bottom, delta=delta/2)
        point(0, r2 + 2r, "(0,r2+2r)", :magenta, :center, :bottom, delta=delta/2)
        point(0, r2 + r, "小円:r\n(0,r2+r)", :red, :center, delta=-delta/2)
        point(x2, r2 - r, "小円:r\n(x2,r2-r)", :red, :center, delta=-delta/2)
        point(2r2 - 2r, 0, "小円:r\n(2r2-2r,0)", :red, :center, delta=-delta/2)
        point(r2 - r, 0, "大円:r2\n(r2-r,0)", :blue, :center, delta=2.5delta)
        point(r - r2, 0, "大円:r2\n(r-r2,0)", :blue, :center, delta=2.5delta)
    end
end;

draw(1/2, true)

算額（その1606）

算額（その1606）

長野県須坂市 とある廃寺 元治元年(1864)
深川英俊，トニー・ロスマン：聖なる数学：算額，森北出版株式会社，2010年４月22日.
キーワード：直角三角形，円弧，正方形，最大値
#Julia, #SymPy, #算額, #和算, #数学

直角三角形の中に円弧を描き，頂点が円弧と斜辺に接する正方形を容れる。股が一定のとき，正方形の一辺の長さは鈎の長さに応じて変化する。正方形の一辺の長さが最大になるのはどのようなときか。

鈎，股をそのまま変数名とする。
正方形の一辺の長さを a, 左下の頂点の座標を (x, 0)
とおき，以下の連立方程式を解く。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy
@syms 鈎::positive, 股::positive,
      x::positive, a::positive
eq1 = (股 -x - a)^2 + (鈎 - a)^2 - 鈎^2
eq2 = a/x - 鈎/股
res = solve([eq1, eq2], (a, x))[2]  # 2 of 2

    (股^2*鈎/(股^2 + 2*股*鈎 + 2*鈎^2), 股^3/(股^2 + 2*股*鈎 + 2*鈎^2))

# 正方形の一辺の長さが最大になるときの鈎
ans_鈎 = solve(diff(res[1], 鈎), 鈎)[1]
ans_鈎 |> println

    sqrt(2)*股/2

# 正方形の一辺の長さの最大値
res[1](鈎 => ans_鈎) |> simplify |> factor |> println

    股*(-1 + sqrt(2))/2

鈎 = 股*√2/2 のとき，正方形の一辺の長さは最大値の「股*(√2 - 1)/2」を取る。

# x 正方形の位置
res[2](鈎 => ans_鈎) |> simplify |> factor |> println

    -股*(-2 + sqrt(2))/2

股 = 10 のとき，鈎 = 7.07107;  正方形の一辺の長さ = 2.07107 である。

function draw(股, more=false)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
    鈎 = √2股/2
    a = 股*(√2 - 1)/2
    x = -股*(-2 + sqrt(2))/2
    θ = atand(股/鈎)
    @printf("股 = %g;  鈎 = %g;  正方形の一辺の長さ = %g\n", 股, 鈎, a)
    plot([0, 股, 股, 0], [0, 0, 鈎, 0], color=:green, lw=0.5)
    plot!([x, x + a, x + a, x, x], [0, 0, a, a, 0], color=:blue, lw=0.5)
    circle(股, 鈎, 鈎, beginangle=270 - θ, endangle=270)
    if more
        delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
        hline!([0], color=:gray80, lw=0.5)
        vline!([0], color=:gray80, lw=0.5)
        point(x, 0, "x", :blue, :center, delta=-delta)
        point(x + a, 0, "x+a", :blue, :center, delta=-delta)
        point(x + a, a, " (x+a,a)", :blue, :left, :vcenter)
        point(x, a, "(x,a)", :blue, :right, :vcenter)
        point(0, 0, "0", :blue, :center, delta=-delta)
        point(股, 0, "股", :blue, :center, delta=-delta)
        point(股, 鈎, "(股,鈎)", :blue, :right, :bottom, delta=delta/2)
        ylims!(-5delta, 股 + delta)
    end
end;

draw(10, true)