【R前処理講座12】{tibble}データフレームの進化版【tidyverse】
https://datasciencemore.com/tibble/
# tribbleを使用して，Markdownチックな表記でtibbleが作成できます．
using RCall
R"""
library(dplyr)
trb = tribble(
~No., ~language,
#-----|---|----
1, "R",
2, "Python",
3, "Julia"
)
"""
trb
Julia だと，
using CSV, DataFrames
data = """
No., language
1, "R"
2, "Python"
3, "Julia"
"""
df = CSV.read(IOBuffer(data), DataFrame)
The forward pipe operator is motivated by the pipe introduced in the magrittr package, but is more streamlined. It is similar to the pipe or pipeline operators introduced in other languages, including F#, Julia, and JavaScript.
【R前処理講座19】{dplyr} group_by：グルーピング【tidyverse】
https://datasciencemore.com/dplyr-group-by/
以下のようなデータフレームにおいて，グループごとの基礎統計量を求める。
まずは 1 変数でグループ化する場合。
using RCall
R"""
library(dplyr)
# define dataframe
df =
tibble(
class = c("a", "b", "c", "c", "a", "c", "b", "a", "c", "b", "a", "x"),
gender = c("M", "F", "F", "M", "F", "M", "M", "F", "M", "M", "F", "F"),
height = c(162, 150, 168, 173, 162, 198, 182, 154, 175, 160, 172, 157)
)
"""
#=
RObject{VecSxp}
# A tibble: 12 x 3
class gender height
1 a M 162
2 b F 150
3 c F 168
4 c M 173
5 a F 162
6 c M 198
7 b M 182
8 a F 154
9 c M 175
10 b M 160
11 a F 172
12 x F 157
=#
まずは class ごとに height の平均値を求める。
R でやると以下のようになる。
パイプの最後を print.data.frame にしているのは，結果が tibble で，それをデフォルトの print.tbl_df が使われてしまい小数点以下の桁数の表示に支障をきたすので，data.frame として出力するためである。
R"""
df %>%
group_by(class) %>%
summarise(mean = mean(height)) %>%
print.data.frame
""";
#=
class mean
1 a 162.5
2 b 164.0
3 c 178.5
4 x 157.0
=#
Julia でやってみよう。
using DataFrames
df = DataFrame(class = ["a", "b", "c", "c", "a", "c", "b", "a", "c", "b", "a", "x"],
gender = ["M", "F", "F", "M", "F", "M", "M", "F", "M", "M", "F", "F"],
height = [162, 150, 168, 173, 162, 198, 182, 154, 175, 160, 172, 157]
);
やり方は何通りかある。
グループ化 groupby() と combine() を 分ける書き方。
最後の |> println は表示形式を若干簡単にするためのものなので，REPL の場合はなくてもよい。
using Statistics
gdf = groupby(df, :class);
combine(gdf, :height=>mean=>:mean) |> println
#=
4×2 DataFrame
Row │ class mean
│ String Float64
─────┼─────────────────
1 │ a 162.5
2 │ b 164.0
3 │ c 178.5
4 │ x 157.0
=#
関数を入れ子にする書き方。出力は同じなので省略。
combine(groupby(df, :class), :height=>mean=>:mean) |> println
パイプを使う書き方。
groupby(df, :class) |> x -> combine(x, :height=>mean=>:mean) |> println
@chain マクロを使う書き方。
using DataFramesMeta # Chain もエクスポートされる
@chain df begin
groupby(:class)
combine(:height=>mean=>:mean)
println
end
複数の変数でグループ化して基本統計量を求める。
まずは R の場合
R"""
df %>%
group_by(class, gender) %>%
summarise(mean = mean(height), .groups="keep") %>%
print.data.frame
""";
#=
class gender mean
1 a F 162.6667
2 a M 162.0000
3 b F 150.0000
4 b M 171.0000
5 c F 168.0000
6 c M 182.0000
7 x F 157.0000
=#
Julia では，何通りかの書き方がある。
関数を入れ子にする書き方。
println(sort(combine(groupby(df, [:class, :gender]), :height=>mean=>:mean)))
#=
7×3 DataFrame
Row │ class gender mean
│ String String Float64
─────┼─────────────────────────
1 │ a F 162.667
2 │ a M 162.0
3 │ b F 150.0
4 │ b M 171.0
5 │ c F 168.0
6 │ c M 182.0
7 │ x F 157.0
=#
パイプを使う書き方。
groupby(df, [:class, :gender]) |> x -> combine(x, :height=>mean=>:mean) |> sort |> println
@chain マクロを使う書き方。
@chain df begin
groupby([:class, :gender])
combine(:height=>mean=>:mean)
sort
println
end
ところで，今までの出力例はちょっとわかりにくい。
以下のようにすれば，表形式で表示できる。このようにすることにより，存在しない組み合わせがあることに気づくことができる。つまり，class = "x", gender = "M" は存在しないということである。セルには missing が表示される。
aggregate = sort(combine(groupby(df, [:class, :gender]), :height=>mean=>:mean));
unstack(aggregate, :class, :gender, :mean) |> println
#=
4×3 DataFrame
Row │ class F M
│ String Float64? Float64?
─────┼─────────────────────────────
1 │ a 162.667 162.0
2 │ b 150.0 171.0
3 │ c 168.0 182.0
4 │ x 157.0 missing
=#
度数も求めることができる。
aggregate2 = sort(combine(groupby(df, [:class, :gender]), :height=>length=>:n));
unstack(aggregate2, :class, :gender, :n) |> println
#=
4×3 DataFrame
Row │ class F M
│ String Int64? Int64?
─────┼─────────────────────────
1 │ a 3 1
2 │ b 1 2
3 │ c 1 3
4 │ x 1 missing
=#
なお，度数の場合は FreqTables::freqtable() で求めるのが簡単である。
using FreqTables
freqtable(df, :class, :gender)
#=
4×2 Named Matrix{Int64}
class ╲ gender │ F M
───────────────┼─────
a │ 3 1
b │ 1 2
c │ 1 3
x │ 1 0
=#
平均値以外の基本統計量を求める。
まずは，R で。
R"""
df %>%
group_by(class) %>%
summarise(
Max = max(height),
Q3 = quantile(height, 0.75),
Mean = mean(height),
Median = median(height),
Q1 = quantile(height, 0.25),
Min = min(height),
sd = sd(height),
n = n()
) %>%
print.data.frame
""";
#=
class Max Q3 Mean Median Q1 Min sd n
1 a 172 164.50 162.5 162 160.00 154 7.371115 4
2 b 182 171.00 164.0 160 155.00 150 16.370706 3
3 c 198 180.75 178.5 174 171.75 168 13.329166 4
4 x 157 157.00 157.0 157 157.00 157 NA 1
=#
Julia もほぼ同じ程度の書き方でできる。
@chain df begin
groupby(:class)
@combine begin
:Max = maximum(:height)
:Q3 = quantile(:height, 0.75)
:Mean = mean(:height)
:Median = median(:height)
:Q1 = quantile(:height, 0.25)
:Min = minimum(:height)
:SD = std(:height)
:n = length(:height)
end
println
end
#=
4×9 DataFrame
Row │ class Max Q3 Mean Median Q1 Min SD n
│ String Int64 Float64 Float64 Float64 Float64 Int64 Float64 Int64
─────┼────────────────────────────────────────────────────────────────────────────
1 │ a 172 164.5 162.5 162.0 160.0 154 7.37111 4
2 │ b 182 171.0 164.0 160.0 155.0 150 16.3707 3
3 │ c 198 180.75 178.5 174.0 171.75 168 13.3292 4
4 │ x 157 157.0 157.0 157.0 157.0 157 NaN 1
=#
上の @chain マクロを使った書き方は，以下のように展開される。
以下を実行すれば，同じ結果が得られる。
combine(groupby(df, :class),
:height => maximum => :Max,
:height => (x -> quantile(x, 0.75)) => :Q3,
:height => mean => :Mean,
:height => median => :Median,
:height => (x -> quantile(x, 0.25)) => :Q1,
:height => minimum => :Min,
:height => std => :SD,
nrow => :n
) |> println
combine() は，以下のようにまとめて書くこともできる。
combine(groupby(df, :class),
fill(:height, 8) .=>
[maximum, (x -> quantile(x, 0.75)), mean, median,
(x -> quantile(x, 0.25)), minimum, std, length] .=>
[:Max, :Q3, :Mean, :Median, :Q1, :Min, :SD, :n]) |> println
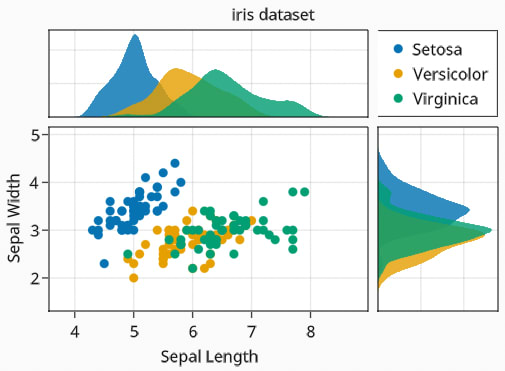
この記法を用いて，すべての変数についての基礎統計料を得ることができる。
using DataFrames, RDatasets
iris = dataset("datasets", "iris");
for i in [:SepalLength, :SepalWidth, :PetalLength, :PetalWidth]
println("\nStatistic of $i")
combine(groupby(iris, :Species),
i => maximum => :Max,
i => (x -> quantile(x, 0.75)) => :Q3,
i => mean => :Mean,
i => median => :Median,
i => (x -> quantile(x, 0.25)) => :Q1,
i => minimum => :Min,
i => std => :SD,
nrow => :n
) |> println
end
#=
Statistic of SepalLength
3×9 DataFrame
Row │ Species Max Q3 Mean Median Q1 Min SD n
│ Cat… Float64 Float64 Float64 Float64 Float64 Float64 Float64 Int64
─────┼───────────────────────────────────────────────────────────────────────────────────
1 │ setosa 5.8 5.2 5.006 5.0 4.8 4.3 0.35249 50
2 │ versicolor 7.0 6.3 5.936 5.9 5.6 4.9 0.516171 50
3 │ virginica 7.9 6.9 6.588 6.5 6.225 4.9 0.63588 50
Statistic of SepalWidth
3×9 DataFrame
Row │ Species Max Q3 Mean Median Q1 Min SD n
│ Cat… Float64 Float64 Float64 Float64 Float64 Float64 Float64 Int64
─────┼───────────────────────────────────────────────────────────────────────────────────
1 │ setosa 4.4 3.675 3.428 3.4 3.2 2.3 0.379064 50
2 │ versicolor 3.4 3.0 2.77 2.8 2.525 2.0 0.313798 50
3 │ virginica 3.8 3.175 2.974 3.0 2.8 2.2 0.322497 50
Statistic of PetalLength
3×9 DataFrame
Row │ Species Max Q3 Mean Median Q1 Min SD n
│ Cat… Float64 Float64 Float64 Float64 Float64 Float64 Float64 Int64
─────┼───────────────────────────────────────────────────────────────────────────────────
1 │ setosa 1.9 1.575 1.462 1.5 1.4 1.0 0.173664 50
2 │ versicolor 5.1 4.6 4.26 4.35 4.0 3.0 0.469911 50
3 │ virginica 6.9 5.875 5.552 5.55 5.1 4.5 0.551895 50
Statistic of PetalWidth
3×9 DataFrame
Row │ Species Max Q3 Mean Median Q1 Min SD n
│ Cat… Float64 Float64 Float64 Float64 Float64 Float64 Float64 Int64
─────┼───────────────────────────────────────────────────────────────────────────────────
1 │ setosa 0.6 0.3 0.246 0.2 0.2 0.1 0.105386 50
2 │ versicolor 1.8 1.5 1.326 1.3 1.2 1.0 0.197753 50
3 │ virginica 2.5 2.3 2.026 2.0 1.8 1.4 0.27465 50
=#
dplyrでカラム名や値を変数で指定してもうまく認識されない
https://trunk28.com/dplyr_for/
引用元の記事は 2021/07/11 のものであるが，「dplyrでカラム名や値を変数で指定してもうまく認識されない」ということで，以下のプログラムはエラーになると...
library(dplyr)
hoge <- names(iris)[1]
iris %>% select(hoge)
エラー: Can't subset columns that don't exist.
x Column `hoge` doesn't exist.
しかし，R 4.2.0 では，以下の "Note" が出るが，一応正しい結果が得られる。
Note: Using an external vector in selections is ambiguous.
ℹ Use `all_of(hoge)` instead of `hoge` to silence this message.
ℹ See <https://tidyselect.r-lib.org/reference/faq-external-vector.html>.
This message is displayed once per session.
解決法として以下のプログラムが提示されているが，.data[[hoge]] のようなわかりにくいものの説明をしている（.data というのは処理中のデータフレームの代名詞だとか）
追記 2022/03/30
中澤先生からのコメントがありました。ありがとうございます。
> hoge <- names(iris)[1]
> iris[,hoge] |> head()
[1] 5.1 4.9 4.7 4.6 5.0 5.4
R"""
library(dplyr)
hoge <- names(iris)[1]
iris %>% select(.data[[hoge]]) %>% head()
"""
RObject{VecSxp}
Sepal.Length
1 5.1
2 4.9
3 4.7
4 4.6
5 5.0
6 5.4
しかも，select, group_by, summarise, relocate の場合は .data[[hoge]] でよいが，
mutate, transmute では mutate("{hoge2}":=Petal.Length+1) などとしなければならないなど，統一性がない。
正攻法は，警告メッセージにもあるが，all_of(hoge) を使うこと。これならまあ許せる。が，mutate, transmute ではこれも動かない。
R"""
library(dplyr)
hoge <- names(iris)[1]
iris %>% select(all_of(hoge)) %>% head()
"""
"Using an external vector in selections is ambiguous." ということだが，プログラム全体を見渡せば，hoge がカラム名でないことは明らかだと思うがなぁ。
Julia ではなんの問題もなく動く（当たり前だ）。
using DataFrames, RDatasets
iris = dataset("datasets", "iris");
hoge = names(iris)[1]
select(iris, hoge) |> x -> first(x, 5)
select() を使う必然性はまったくなく，iris[:, hoge] で十分。
Juliaをもっと速くしよう！
https://zenn.dev/ohno/articles/0ba7970d419898
「多次元配列のメモリ上の位置は Julia, R, Fortran では（Python と違い）列優先なので，bad よりは，内側の for ループでは左側の添字を変化させる good のほうが速い」と書かれている。筆者は Windows のようであり，確かに good のほうが速いという結果が提示されている。
私の環境は Mac mini M1 チップなのだが，両者の違いは殆どなかった。
function bad(arr)
sum = 0
for i in 1:size(arr)[1]
for j in 1:size(arr)[2]
sum += arr[i,j]
end
end
return sum
end
function good(arr)
sum = 0
for j in 1:size(arr)[2]
for i in 1:size(arr)[1]
sum += arr[i,j]
end
end
return sum
end
実は，例に挙げられた関数はもっと早くなる。
sum = 0
を
sum = zero(eltype(arr))
にするだけだ。 sum = 0.0 でもよい。
「Julia は動的型付け言語じゃないか。sum = 0 のどこが悪い?」という人もいると思うが，
sum = 0 だと，sum は Union{Float64, Int64} になってしまう。
sum = zero(eltype(arr)) なら Float64 だ。
余計なことをしないで済むぶん，後者のほうが 6 倍ほど速い。
今更ながらではあるが，
R の
> rep(1:3, each=3)
[1] 1 1 1 2 2 2 3 3 3
> rep(1:3, 3)
[1] 1 2 3 1 2 3 1 2 3
Julia では
julia> repeat([1,2,3], inner=3)
9-element Vector{Int64}:
1
1
1
2
2
2
3
3
3
julia> repeat([1,2,3], outer=3)
9-element Vector{Int64}:
1
2
3
1
2
3
1
2
3
julia> repeat([1,2,3], 3)
9-element Vector{Int64}:
1
2
3
1
2
3
1
2
3
ついでに
julia> repeat(1:3, inner=2, outer=3)
18-element Vector{Int64}:
1
1
2
2
3
3
1
1
2
2
3
3
1
1
2
2
3
3
https://p-suugaku.blogspot.com/2022/03/yx2y2x3.html
ですが，煎じ詰めれば，x^2 = 2^x の解を求めるということ。
元記事では第 3 の解をニュートン法を使って（しかも Google スプレッドシートを用いて）求めている。
SymPy を使うと以下のようになる。
ulia> using SymPy
julia> @syms x
(x,)
julia> eq = Eq(x^2, 2^x)
2 x
x = 2
julia> a = solve(eq)
3-element Vector{Sym}:
2
4
-2*LambertW(log(2)/2)/log(2)
julia> a[3].evalf()
-0.766664695962123
3 番目の解は，-2*LambertW(log(2)/2)/log(2) ということではあるが，
a[3].evalf() = -0.766664695962123
ということですね。
> ただし、これはあくまで近似解だという点は留意すべきです。
> Googleスプレッドシートで計算で扱えるのは15桁までのようで、その限られた桁数で計算していたため値が収束しているように見えたに過ぎません。
> なので、収束したからと言って真の解を得たとはいえませんが、十分参考になると思います。
> 微分と表計算ソフトの知識さえあれば簡単に近似解を求められるので、試してみてください。
と，控えめ？な表現ですが，解析解でなくても数値解で十分ですよね。
逆に，-2*LambertW(log(2)/2)/log(2) ですって言われても，今の私には，ワケワカメ。
julia> using LambertW
julia> -2*lambertw(log(2)/2)/log(2)
-0.766664695962123
https://data-viz-lab.com/ggplot2
であるが，色々あって，最終的には
が成果物として挙げられている。
所要のプログラムは 51 行とのこと（キータッチ数は結構あるなあ）。
結構細かい指定が一杯ある。
とても，「簡単にきれいな図が得られます」とは言えないような。
# First draw a basic plot with main arguments
plot <- ggplot(data = data_iris, #set the data
mapping = aes(x=Sepal.Length, #set x axis
y=Petal.Length, #set y axis
colour=Species) #set color by species
) +
geom_point() + #set a scatter plot
geom_smooth(method = "lm") #set a linear line
# Then make it nicer
plot <- plot +
theme(axis.line = element_line(colour = "black", #set color of axis line
size = 0.7, #size
linetype = "solid"), #and line type
legend.justification = c(1, 1), #set legend inside plot
legend.position= c(1, 0.5), #set position by x and y axis
legend.title = element_text(size = 12, color = "black",
face = "bold"),
legend.text = element_text(size = 10, color = "black",
face = c("italic")),
legend.background = element_blank(),
legend.key = element_blank(),
legend.box.background = element_rect(colour = "black"),
panel.grid.major = element_blank(),
panel.grid.minor = element_blank(),
panel.background = element_blank()
) +
labs(title="Association between the length of petal and setal",
subtitle="From IRIS dataset") +
scale_x_continuous(name = "Lenght of Sepal (cm)",
breaks = seq(4,8,1),
limits = c(4,8)
) +
scale_y_continuous(name = "Lenght of Petal (cm)",
breaks = seq(0, 8, 1),
labels = seq(0, 8, 1),
limits = c(0, 8)) +
theme(axis.title.x = element_text(size = 12, hjust = 0.5),
axis.text.x = element_text(size = 12),
axis.text.y = element_text(size = 12),
axis.title.y=element_text(size=12, vjust = 0.8),
plot.title = element_text(size = 12, #font size and adjust
hjust = 0.5,#adjust
face = "bold"),
plot.subtitle = element_text(size = 10, #font size and adjust
hjust = 0.5,#adjust
face = "bold")
) +
scale_colour_viridis(discrete = TRUE, alpha=0.6)
plotJulia では，前回のプログラムを少し修正して，複数のデータフレームでの描画を蓄積して最終結果を表示するという戦略を立てた。
まずは，scatterplot() のバージョンアップ版
function scatterplot(df; xlabel="", ylabel="", grouplabel="", col=:black, conflevel=0.95,
add=false) # append
gr( tick_direction=:out,
grid=false,
markerstrokewidth=0,
alpha=0.4,
fontfamily="serif",
guidefontfamily="times",
guidefontsize=8,
titlefontfamily="times", # append
titlefontsize=10, # append
label="")
df2 = DataFrame(x=df[:,1], y=df[:,2])
model = lm(@formula(y ~ x), df2);
minx, maxx = extrema(df2.x)
pred = DataFrame(x=range(minx, maxx, length=500));
pr = predict(model, pred, interval=:confidence, level=conflevel);
add || (p = plot(xlabel=xlabel, ylabel=ylabel)) # append
p = scatter!(df2.x,
df2.y,
color=col);#,
#xlabel=xlabel, # delete
#yaxis=ylabel); # delete
plot!( pred.x,
pr.prediction,
linecolor=:red,
linewidth=2,
color=:gray,
ribbon=(pr.prediction .- pr.lower,
pr.upper .- pr.prediction))
for gl in grouplabel
annotate!(gl[1],
gl[2],
text(gl[3],
"times",
8,
gl[4]))
end
p
end
これを使うにあたっての事前準備。まあ，単にデータフレームの分割であるが。
gd = groupby(iris, :Species);
続いては，分割されたデータフレームについて scatterplot() を呼び出す。
ただし，2 つ目以降は，グラフの追加（add=true）。
for i in 1:length(gd)
scatterplot(gd[i][:,[:SepalLength, :PetalLength]],
xlabel="Length of Sepal(cm)",
ylabel="Length of Petal(cm)",
grouplabel=[[(5.5, 2.2, "Setosa", :red),
(6.5, 3.8, "Versicolor", :green),
(6.0, 6.4, "Virginica", :blue)][i]],
col=[:red, :green, :blue][i],
add=i != 1)
end
最後に，タイトルを付けておきましょう。
title!("Association between the length of petal and sepal\nFrom IRIS dataset")
出来上がりは，以下の通り。
ggplot2 の入門ということで定番の図であるが，
https://data-viz-lab.com/ggplot2
にも以下の図がある。
書くのは簡単だよと
> plot <- ggplot(data = data_iris,
+ mapping = aes(x=Sepal.Length,
+ y=Petal.Length)) +
+ geom_point(aes(colour=Species)) +
+ geom_smooth(method = "lm",
+ colour="pink")
> plot
が挙げられているが，なんか知らないが，データフレームを専用に変換しないといけないとかで，事前にいかが必要とのこと。
> # データセットのリストを作成
> l <- data()
> results <- l$results %>%
+ as.data.frame()
> list <- results$Item
>
> # ループ処理でデータセットをデータフレーム型に変換
> for (i in list) {
+ data <- try(get(i), silent = TRUE) %>% # Use try function to ignore errors
+ try(as.data.frame(), silent = TRUE)
+ if (is.data.frame(data)==TRUE) {
+ name <- paste0("data_", i)
+ assign(name, data)
+ } else {
+ }
+ }
Julia でなるべく汎用性をもたせるように関数を書いてみた。
using Plots
using DataFrames, GLM
function scatterplot(df; xlabel="", ylabel="", grouplabel="", col=:black, conflevel=0.95)
gr( tick_direction=:out,
grid=false,
markerstrokewidth=0,
alpha=0.4,
fontfamily="serif",
guidefontfamily="times",
guidefontsize=8,
label="")
df2 = DataFrame(x=df[:,1], y=df[:,2])
model = lm(@formula(y ~ x), df2);
minx, maxx = extrema(df2.x)
pred = DataFrame(x=range(minx, maxx, length=500));
pr = predict(model, pred, interval=:confidence, level=conflevel);
p = scatter(df2.x,
df2.y,
color=col,
xlabel=xlabel,
yaxis=ylabel);
plot!( pred.x,
pr.prediction,
linecolor=:red,
linewidth=2,
color=:gray,
ribbon=(pr.prediction .- pr.lower,
pr.upper .- pr.prediction))
for gl in grouplabel
annotate!(gl[1],
gl[2],
text(gl[3],
"times",
8,
gl[4]))
end
p
end
scatterplot() にあたえるのは，2列のデータフレーム（一応，1列目が x 軸，2列目が y 軸に対応するものとしておく）
キーワード引数は
x, y 軸の名前 xlabel="", ylabel="",
各グループのアノテーションのタプル (x 座標，y 座標，グループの名前，文字色）のベクトル grouplabel="",
グループを表示する色 col=:black,
信頼限界帯の信頼率 conflevel=0.95
最低限では2列のデータフレームを渡すだけ。
using RDatasets
iris = dataset("datasets", "iris");
palette = [:red, :green, "blue"];
col = repeat(palette, inner=50);
scatterplot(iris[:, [:SepalLength, :PetalLength]])
先程のサイトと同じように描くときは
scatterplot(iris[:, [:SepalLength, :PetalLength]],
xlabel="Sepal Length",
ylabel="Petal Length",
grouplabel=[(5.5, 2.2, "Setosa", :red),
(6.5, 3.8, "Versicolor", :green),
(6.0, 6.4, "Virginica", :blue)],
col=col)
まあ，ggplot() が scatterplot() に相当するのだから，scatterplot() の呼び出しが 7 行（実質は 2, 3 行）というのはむしろ短い。汎用性もあるし。
出来上がった図は，好みの差もあるが Julia に軍配があがるだろう。
> だからCMSは嫌いだ。自分でhtmlやcgiを書いてWinSCPでアップロードする方が何がどうなっているかちゃんとわかるし、ずっと楽だ。なぜCMSがこんなに流行るのか理解できない。Rのグラフィクスでbaseが好きな自分にはggplot2がもてはやされるのが理解できないのだが、それと同じ感覚。たぶん自分がズレているのだが。
いえいえ，いまの潮流が本筋からずれているだけだと思いましょう。
ggplot2 に限らず，tidyverse とか tidydata とかなんとか，わけも分からずグラフックの王道もわからずいいかんげんなグラフを再生産させ続けている御本尊にも相当な責任があると思います。新興宗教的なところがあると思います。
Julia に限らないのだけれど
if myrank == 0
a1 = ones(n)
else
a1 = 2*ones(n)
end
などというのがあると，いやーな気分になる
a1 = ones(n)
myrank != 0 && (a1 *= 2)
とか書きたくなる。病気だなあ。
method=:cov の場合と method=:svd の場合の結果が違うという指摘に答えてくれて，
MultivariateStats v0.9.1 へバージョンアップされた。
それに伴い，以下を修正した。
https://blog.goo.ne.jp/r-de-r/e/5e04aee16df93634f81a13d0dd3d5f45
https://r-de-r.github.io/stats/Julia-stats8.html
なにはともあれ，実際に見てもらいましょう。
ノートブック（Jupyter lab など）に似ているけど，プログラミング中の変数値を変えると，関連する計算式の結果も変わる。ちょうど，Excel でセルの値を変えると他のセルの結果も変わるように。
間違えたら間違った結果が出るので，どこをどう直したらどうなるかがすぐわかる。プログラミングの学習に役立つかな。
また，一度作っておけば簡易電卓みたいに入力データだけ変えて結果を得るとかにも使えそう。
コーディング部分は見えないようにもできる。
中澤先生が言及されていた NSM3:::kendall.ci() であるが，
> bootstrap=TRUEと指定すれば（B=でシミュレーション回数）ブートストラップ推定もできるというすぐれものだが、
> 欠損値対応していないこと（欠損値を含むデータを与えるとエラーになる）、
> 信頼区間だけ表示されて点推定量が表示されないこと
意外にも，プログラミング的にはダメダメなプログラムであった。最後に書き換えたプログラムを置いておくが，
欠損値対応は
ok = complete.cases(x, y)
x = x[ok]
y = y[ok]
の 3 行でできるし，
点推定量は求めているのに表示していないだけなので，cat() で書き出すだけ。
問題は，ブートストラップの部分。私の環境で example=TRUE, B=60000 でブートストラップをすると，31 秒かかった。
速度を上げるにはまず，cor.test() ではなく，以前にも書いた pcaPP の cor.fk() を使う。これで 6 秒くらいになった。
更に，毎回の結果を tau <- c(tau, tau.sample) で保存しているのだが，これは前もって必要なメモリを確保して tau[b] = tau.sample するのが定石。これで，0.865 秒になった。元の版から比べて，35 倍速になったということだ。
ちなみに，Julia で書いたら 0.06 秒なので 500 倍速だが。
誰か，原作者に教えてあげて。
# cor.test ではなく pcaPP の cor.fk を使う
library(pcaPP)
kendall.ci2 = function (x = NULL, y = NULL, alpha = 0.05, type = "t", bootstrap = FALSE,
B = 1000, example = FALSE)
{
if (example) {
x <- c(44.4, 45.9, 41.9, 53.3, 44.7, 44.1, 50.7, 45.2,
60.1)
y <- c(2.6, 3.1, 2.5, 5, 3.6, 4, 5.2, 2.8, 3.8)
}
# 欠損値対を除くために3行追加
ok = complete.cases(x, y)
x = x[ok]
y = y[ok]
n = length(x)
if (n <= 1) {
cat("\n")
cat("Sample size n must be at least two!", "\n")
cat("\n")
return # エラーなら即戻る
} else if (is.null(x) | is.null(y)) {
cat("\n")
cat("You must supply an x sample and a y sample!", "\n")
cat("\n")
return
} else if (n != length(y)) {
cat("\n")
cat("Samples must be of the same length!", "\n")
cat("\n")
return
} else if (type != "t" && type != "l" && type != "u") {
cat("\n")
cat("Argument \"type\" must be one of \"t\" (two-sided), \"l\" (lower) or \"u\" (upper)!",
"\n")
cat("\n")
return
}
Q <- function(xi, yi, xk, yk) { # 引数展開
ij <- (yk - yi) * (xk - xi)
if (ij > 0)
return(1)
if (ij < 0)
return(-1)
0
}
C.i <- function(x, y, i) {
C.i <- 0
for (k in 1:length(x)) if (k != i)
C.i <- C.i + Q(x[i], y[i], x[k], y[k])
C.i
}
# cor.test ではなく cor.fk を使う
# tau.hat <- cor.test(x, y, method = "k")$estimate
tau.hat <- cor.fk(x, y)
kendall.tau <- tau.hat # 後で結果出力するために取っておく
if (!bootstrap) {
c.i <- numeric(0)
for (i in 1:n) c.i <- c(c.i, C.i(x, y, i))
#options(warn = -1)
#options(warn = 0)
sigma.hat.2 <- 2 * (n - 2) * var(c.i)/n/(n - 1)
sigma.hat.2 <- sigma.hat.2 + 1 - (tau.hat)^2
sigma.hat.2 <- sigma.hat.2 * 2/n/(n - 1)
if (type == "t") {
z <- qnorm(alpha/2, lower.tail = FALSE)
} else { #if (type != "t")
z <- qnorm(alpha, lower.tail = FALSE)
}
tau.L <- tau.hat - z * sqrt(sigma.hat.2)
tau.U <- tau.hat + z * sqrt(sigma.hat.2)
} else {
# append するのではなく前もって必要メモリ確保
# こうするだけで，実行時間が 1/5 になる!
tau <- numeric(B)
for (b in 1:B) {
# sample() の第1引数は 1:n ではなく n とする
b.sample <- sample(n, n, replace = TRUE)
# cor.test ではなく cor.fk を使う
#options(warn = -1)
#tau.sample <- cor.test(x[b.sample], y[b.sample],
# method = "k")
#options(warn = 0)
#tau.sample <- tau.sample$estimate
tau[b] <- cor.fk(x[b.sample], y[b.sample])
}
tau.hat <- sort(tau)
# hist(tau.hat)
if (type == "t") {
k <- floor((B + 1) * alpha/2)
} else { #if (type != "t")
k <- floor((B + 1) * alpha)
}
tau.L <- tau.hat[k]
tau.U <- tau.hat[(B + 1 - k)]
}
# tau.L <- round(tau.L, 3)
# tau.U <- round(tau.U, 3)
cat("\nn =", n, ", kendall tau =", kendall.tau,"\n")
if (type == "t") {
print.type <- " two-sided CI for tau:"
} else if (type == "l") {
tau.U <- 1
print.type <- " lower bound for tau:"
} else { # (type == "u")
tau.L <- -1
print.type <- " upper bound for tau:"
}
cat("\n")
cat("1 - alpha = ", 1 - alpha, print.type)
cat("\n")
cat(tau.L, ", ", tau.U, "\n")
cat("\n")
}
kendall.ci2(example=TRUE)
# 1 - alpha = 0.95 two-sided CI for tau:
# -0.05255393, 0.9414428
#VVVVVVVVVVVVVVVVVVVVVVVVVVVVVVVVVVVV
# n = 9 , kendall tau = 0.4444444
#
# 1 - alpha = 0.95 two-sided CI for tau:
# -0.05255393 , 0.9414428
system.time(kendall.ci2(bootstrap=TRUE, B= 60000, example=TRUE))
# 1 - alpha = 0.95 two-sided CI for tau:
# -0.125, 0.93103448275862
#
# user system elapsed
# 30.948 1.308 32.220
#VVVVVVVVVVVVVVVVVVVVVVVVVVVVVVVVVVVV
# n = 9 , kendall tau = 0.4444444
#
# 1 - alpha = 0.95 two-sided CI for tau:
# -0.125 , 0.9310345
#
# user system elapsed
# 0.865 0.007 0.872
#
# 35倍速になった！！
Julia プログラム
using Statistics, StatsBase, Distributions, Plots
function kendall_ci(x, y; alpha = 0.05, type = :both, bootstrap = false,
B = 1000)
n = length(x)
length(x) <= 1 && error("\nSample size n must be at least two!\n")
length(y) != n && error("\nSamples must be of the same length!\n")
isnothing(indexin([type], [:both, :left, :right])[1]) &&
error("\nArgument \"type\" must be one of \":both\" (symmetric), ",
"\":left\" (lower) or \":right\" (upper)!")
function Q(xi, yi, xk, yk)
ij = (yk - yi) * (xk - xi)
ij > 0 && return 1
ij < 0 && return -1
0
end
function C_i(x, y, i)
C = 0
for k in 1:length(x)
k != i && (C += Q(x[i], y[i], x[k], y[k]))
end
C
end
if !bootstrap
c_i = Int[]
for i in 1:n
append!(c_i, C_i(x, y, i))
end
tau_hat = corkendall(x, y)
isnan(tau_hat) && error("corkendall returned 'NaN'")
sigma_hat_2 = 2 * (n - 2) * var(c_i)/n/(n - 1)
sigma_hat_2 += 1 - (tau_hat)^2
sigma_hat_2 *= 2/n/(n - 1)
z = quantile(Normal(), alpha/(type == :both ? 2 : 1))
tau_L, tau_U = tau_hat .+ [1, -1] * z * sqrt(sigma_hat_2)
else
tau = Float64[]
for b in 1:B
b_sample = rand(1:n, n)
tau_sample = corkendall(x[b_sample], y[b_sample])
isnan(tau_sample) || append!(tau, tau_sample)
end
tau_hat = sort(tau)
B = length(tau_hat)
histogram(tau_hat)
k = floor(Int, (B + 1) * alpha/(type==:both ? 2 : 1))
tau_L = tau_hat[k]
tau_U = tau_hat[(B + 1 - k)]
end
if type == :both
print_type = "two-sided CI"
elseif type == :left
print_type = "lower bound"
tau_U = 1
else
print_type = "upper bound"
tau_L = -1
end
println("1 - alpha = $(1 - alpha) $print_type for tau:\n")
println("$tau_L, $tau_U")
end
Julia では，グラフ作成のためのパッケージが色々あるので，少しずつつまみ食いしている。
GRMalie（Makie） を試してみたが，その中では以下のものが目に止まった。
iris データを使って書いてみた。ただし，Makie では，grid を消すことができないそうだ。grid も含めて tick などもまとめて消すことはできるようだが，それでは副作用が大きすぎる。
また，標榜しているほどきれいでもない。
なので，今後も使う予定はない。
using GLMakie
using FileIO
using ColorTypes
using RDatasets
noto_sans = assetpath("fonts", "NotoSans-Regular.ttf")
noto_sans_bold = assetpath("fonts", "NotoSans-Bold.ttf")
f = Figure(backgroundcolor = RGB(0.98, 0.98, 0.98),
resolution = (1000, 700), font = noto_sans)
ga = f[1, 1] = GridLayout()
gb = f[2, 1] = GridLayout()
gcd = f[1:2, 2] = GridLayout()
gc = gcd[1, 1] = GridLayout()
gd = gcd[2, 1] = GridLayout()
axtop = Axis(ga[1, 1])
axmain = Axis(ga[2, 1], xlabel = "Sepal Length", ylabel = "Sepal Width")
axright = Axis(ga[2, 2])
linkyaxes!(axmain, axright)
linkxaxes!(axmain, axtop)
iris = dataset("datasets", "iris")
labels = ["Setosa", "Versicolor", "Virginica"]
data = Array{Float64, 3}(undef, 50, 2, 3);
data[:, :, 1] = Matrix(iris[1:50, 1:2]);
data[:, :, 2] = Matrix(iris[51:100, 1:2]);
data[:, :, 3] = Matrix(iris[101:150, 1:2]);
for (label, col) in zip(labels, eachslice(data, dims = 3))
scatter!(axmain, col, label = label)
density!(axtop, col[:, 1])
density!(axright, col[:, 2], direction = :y)
end
ylims!(axtop, low = 0)
xlims!(axright, low = 0)
leg = Legend(ga[1, 2], axmain)
hidedecorations!(axtop, grid = false)
hidedecorations!(axright, grid = false)
leg.tellheight = true
colgap!(ga, 10)
rowgap!(ga, 10)
Label(ga[1, 1:2, Top()], "iris dataset", valign = :bottom,
padding = (0, 0, 5, 0))
f
