算額（その5）

算額（その5）

群馬県高崎市 幸宮神社 文政7年(1824)
https://blog.goo.ne.jp/r-de-r/e/95e0d587bc8ce1d15512697ad8ad6102

東京都府中市の大国魂神社にも同じ問題（上下が反対）の算額があるが，それは明治 18 年(1885) のものだ。

大円に接する 3 個の正六角形と，大円および正六角形に接する 3 個の円がある。

大円，小円の半径をそれぞれ r, x とする。x を求めよ。

AB = AC + CB = √3/4 \* r + x，OB = r - x とすると，AB / OB = cos(π/6) である。

using SymPy
@syms r::positive, x::positive;

eq1 = (r*sqrt(Sym(3))/4+x) / (r - x) - cos(PI/6);
res = solve(eq1, x);
res[1] |> factor |> println

   r*(-3 + 2*sqrt(3))/2

x = r*(2*√3 - 3)/2 である。

using Plots

function circle2(ox, oy, r; color=:red)
   θ = 0:0.01:2pi
   x = r.*cos.(θ)
   y = r.*sin.(θ)
   plot!(ox .+ x, oy .+ y, color=color)
end;

function hexagon(ox, oy, ol; color=:blue)
   θ = range(pi/6, pi*13/6, length=7)
   sinθ = ol.*sin.(θ).+oy
   cosθ = ol.*cos.(θ).+ox
   plot!(cosθ, sinθ, color=color)
end;

function draw(r=1, more=true)
   pyplot(size=(500, 500), aspectratio=1, label="", fontfamily="IPAMincho")
   pi6 = pi/6
   plot()
   circle2(0, 0, r, color=:black)
   hexagon(0.5r*cos(pi6), 0.5r*sin(pi6), 0.5r)
   hexagon(0.5r*cos(pi6+4pi6), 0.5r*sin(pi6+4pi6), 0.5r)
   hexagon(0.5r*cos(pi6+8pi6), 0.5r*sin(pi6+8pi6), 0.5r)
   x = r*(2*sqrt(3) - 3)/2
   circle2(0, r-x, x)
   circle2((r-x)*cos(7*pi6), (r-x)*sin(7*pi6), x)
   circle2((r-x)*cos(11*pi6), (r-x)*sin(11*pi6), x)
   if more
       plot!([0, r*cos(pi6)], [0, r*sin(pi6)])
       plot!([0, 0], [0, r-x])
       plot!([0, (r-x)/2*cos(pi6)], [r-x, (r-x)/2*sin(pi6)])
       annotate!(0, 0, text("O ", 10, :right, :bottom))
       annotate!((r-x)/2*cos(pi6), (r-x)/2*sin(pi6), text("A", 10, :left, :top))
       annotate!(0, r-x, text(" B", 10, :left, :bottom))
       annotate!(x*sin(pi6), r-(x+x*cos(pi6)), text(" C", 10, :left, :top))
   end
end

draw(1, false)

算額（その4）

算額（その4）

大阪府茨木市 総持寺 嘉永7(1854)年3月
http://www.wasan.jp/osaka/sojiji.html

大阪府茨木市 総持寺 嘉永7(1854)年3月
近畿数学史学会：近畿の算額「数学の絵馬を訪ねて」，平成4年5月16日 初版第一刷，大阪教育図書株式会社，大阪市.

(3) 奈良県大和郡山市小泉町 耳成山口神社 嘉永7年(1854)
近畿数学史学会：近畿の算額「数学の絵馬を訪ねて」，平成4年5月16日 初版第一刷，大阪教育図書株式会社，大阪市.

香川県三豊市豊中町本山 本山寺 万延元年(1860)
http://www.wasan.jp/kagawa/honzanji2.html

六八 川越市石田 藤宮神社 明治4年(1871)
埼玉県立図書館：埼玉県史料集 第二集『埼玉の算額』，昭和44年，誠美堂印刷所，埼玉県与野市.

正三角形の底辺に内接し，隣同士の円も接する3つの円が，更に頂点を通る1つの円とも接するような場合，大円，中円，小円の半径を求めよ。

正三角形の一辺の長さを 2 とし，大円，中円，小円の半径を r1, r2, r3 とし，中円の中心座標を (x2, r2) とする。

using SymPy
@syms r1::positive, r2::positive, r3::positive;
x2 = 1 - √Sym(3)r2;
eq1 = (r2 - r3)^2 + x2^2 - (r2 + r3)^2;
eq2 = 2r1 + 2r3 - √Sym(3);
eq3 = (√Sym(3) - r1 - r2)^2 + x2^2 - (r1 + r2)^2;
res = solve([eq1, eq2, eq3])

   2-element Vector{Dict{Any, Any}}:
    Dict(r2 => sqrt(3), r3 => sqrt(3)/3, r1 => sqrt(3)/6)
    Dict(r2 => sqrt(3)/6, r3 => sqrt(3)/8, r1 => 3*sqrt(3)/8)

r1 > r2 > r3 なので，Dict(r3 => sqrt(3)/3, r2 => sqrt(3), r1 => sqrt(3)/6) は不適切である。

res[1][r1].evalf(), res[1][r2].evalf(), res[1][r3].evalf()

   (0.288675134594813, 1.73205080756888, 0.577350269189626)

Dict(r3 => sqrt(3)/8, r2 => sqrt(3)/6, r1 => 3*sqrt(3)/8) が適切な解である。

res[2][r1].evalf(), res[2][r2].evalf(), res[2][r3].evalf()

   (0.649519052838329, 0.288675134594813, 0.216506350946110)

なお，x2 = 1-√3 r2 = 1-√3 (√3/6) = 0.5 である。

---

using Plots

function circle2(ox, oy, r; color=:red)
   theta = 0:0.01:2pi
   x = r.*cos.(theta)
   y = r.*sin.(theta)
   plot!(ox .+ x, oy .+ y, color=color)
end;

function draw(more)
   sqrt3 = sqrt(3)
   r3 = sqrt3/8
   r2 = sqrt3/6
   r1 = 3sqrt3/8
   println("r1 = $r1,  r2 = $r2,  r3 = $r3")
   x2 = 1-sqrt3*r2  # 0.5
   pyplot(size=(500, 500), aspectratio=1, label="", fontfamily="IPAMincho")
   plot([-1, 1, 0, -1], [0, 0, sqrt3, 0])
   circle2(0, sqrt3-r1, r1)
   circle2(0, r3, r3)
   circle2(x2, r2, r2)
   circle2(-x2, r2, r2)
   if more == true
       scatter!([0, x2, 0, -1+sqrt3*r2], [sqrt3-r1, r2, r3, r2])
       plot!([0, 0], [sqrt3-r1, sqrt3])
       annotate!(0, sqrt3-r1/2, text(" r1", 10, :left))
       plot!([x2, x2], [r2, 0])
       annotate!(x2, r2/2, text(" r2", 10, :left))
       annotate!(x2, 1.2*r2, text("(x2,r2)", 10))
       plot!([-x2, -x2], [r2, 0])
       annotate!(-x2, r2/2, text(" r2", 10, :left))
       plot!([0, 0], [r3, 0])
       annotate!(0, r3/2, text(" r3", 10, :left))
   end
end
draw(true)
   r1 = 3sqrt3/8,  r2 = sqrt3/6,  r3 = sqrt3/8

算額（その3）

算額（その3）

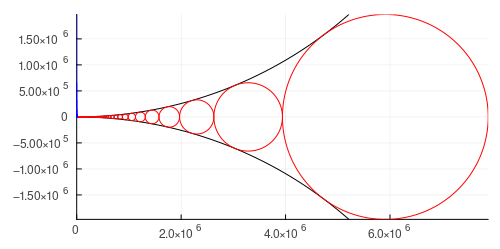
一点で接する半径の等しい弧がある。その弧にはさまれて，それぞれの弧に接し，また隣の円に接するような円を順々に作る。最初の円の直径を四寸，次は五寸とする。黒い部分（最小の円と両弧の間）の面積を最大にした場合，円をいくつはさむことができるか。

「黒い部分（最小の円と両弧の間）の面積を最大にした場合」というのはいらないのではないか？

• i 番目の円の半径 ri，中心座標 (xi, 0)
• i+1 番目の円の半径 rip1，中心座標 (xip1, 0)
• 円の半径を r，中心座標を (0, r) とする。その円の一部が「弧」

using SymPy
@syms r, ri, rip1, xi, xip1, r1::positive, r2::positive, x1::positive, x2::positive

   (r, ri, rip1, xi, xip1, r1, r2, x1, x2)

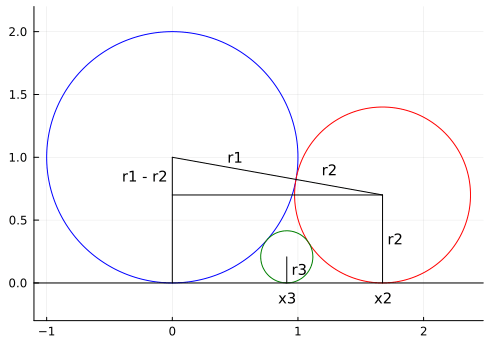
中心座標と半径の関係

xpi1 - xi = rip1 + ri

xpi1 - xi - rip1 - ri = 0 …… （1）

弧が i 番目の円と接することから

(r + ri)^2 = r^2 + xi^2

xi = sqrt(2r * ri + ri^2)
xip1 = sqrt(2r * rip1 + rip1^2) …… （2）

（1) に (2) を代入

a = sqrt(2r * rip1 + rip1^2) - sqrt(2r * ri + ri^2) - rip1 - ri
a |> println

   -ri - rip1 - sqrt(2*r*ri + ri^2) + sqrt(2*r*rip1 + rip1^2)

rip1 について解く。解が円の半径の漸化式になる。

b = solve(a, rip1)[1];
b |> println

   ri*(r + ri + sqrt(ri*(2*r + ri)))/(r - ri - sqrt(ri*(2*r + ri)))

一番小さい円の半径を r1，2 番目に大きい円の半径 r2 とする。

eq1 = (r + r1)^2 - r^2 - x1^2;
eq2 = (r + r2)^2 - r^2 - x2^2;
eq3 = x2 - x1 - r2 - r1;

results = solve([eq1, eq2, eq3], (x1, x2, r));

r1 = 4, r2 = 5 が与えられているので，弧を持つ円の半径は 720 である。

results[1][3](r1 => 4, r2 => 5) |> println

   720

---

using Plots

# 次に大きい円の半径
f(ri, r) = ri*(r + ri + sqrt(ri*(2*r + ri)))/(r - ri - sqrt(ri*(2*r + ri)))

function circle2(ox, oy, r; color=:red)
   theta = 0:0.01:2pi
   x = r.*cos.(theta)
   y = r.*sin.(theta)
   plot!(ox .+ x, oy .+ y, color=color)
end;

function draw(r1, r2)
   r = 4*r1*r2*(r1 + r2)/(r1 - r2)^2
   println("r = $r")
   gr(size=(500, 500), aspectratio=1, label="", fontfamily="IPAMincho")
   plot()
   circle2(0, r, r, color=:black)
   circle2(0, -r, r, color=:black)
   ri = r1
   maxr, maxx = r1, 0
   no = 0
   while r - ri - sqrt(ri*(2*r + ri)) >= 0
       x = sqrt((r + ri)^2 - r^2)  # 半径 ri の円の中心の x 座標
       maxx = max(x, maxx)
       maxr = max(ri, maxr)
       no += 1
       println("$no: x = $x, r = $ri,  $(ri + sqrt(ri*(2*r + ri)))")
       circle2(x, 0, ri)
       plot!([0, 0], [ri, 0], color=:blue)
       ri = f(ri, r)  # その次に大きい円の半径
   end
   println(maxx/maxr)
   plot!(xlims=(0, maxx　+　maxr), ylims=(-maxr, maxr),
         size=(500, 500　*　2maxr　/　(maxx　+　maxr)))
   savefig("$r1-$r2.png")
end

答え：9個の円が存在する

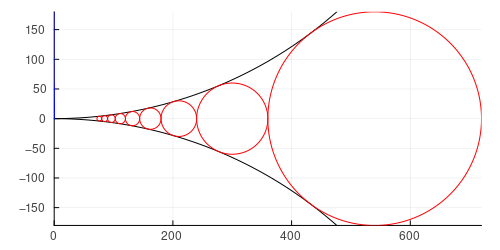
draw(4, 5)

   r = 720.0
   1: x = 76.0, r = 4,  80.0
   2: x = 85.0, r = 5.0,  90.0
   3: x = 96.42857142857166, r = 6.428571428571429,  102.85714285714286
   4: x = 111.42857142857119, r = 8.571428571428573,  120.00000000000001
   5: x = 132.0, r = 12.000000000000002,  144.0
   6: x = 162.0, r = 18.000000000000004,  180.0
   7: x = 210.0, r = 30.000000000000007,  240.00000000000003
   8: x = 300.0, r = 60.000000000000014,  360.0
   9: x = 540.0, r = 180.00000000000003,  720.0
   2.9999999999999996

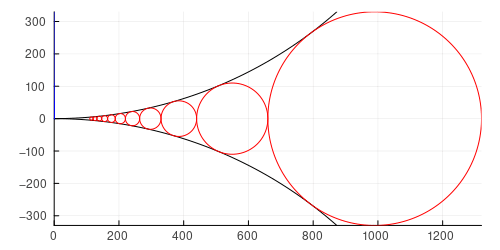
その他の例

draw(5, 6)

   r = 1320.0
   1: x = 115.0, r = 5,  120.0
   2: x = 126.0, r = 6.0,  132.0
   3: x = 139.3333333333324, r = 7.333333333333333,  146.66666666666669
   4: x = 155.833333333334, r = 9.166666666666664,  164.99999999999997
   5: x = 176.78571428571388, r = 11.785714285714283,  188.57142857142853
   6: x = 204.2857142857146, r = 15.714285714285708,  219.99999999999994
   7: x = 242.0, r = 21.99999999999999,  263.99999999999994
   8: x = 297.0, r = 32.999999999999986,  329.99999999999994
   9: x = 385.0, r = 54.99999999999998,  439.99999999999994
   10: x = 550.0, r = 109.99999999999996,  659.9999999999999
   11: x = 989.9999999999995, r = 329.99999999999983,  1319.9999999999995
   3.0

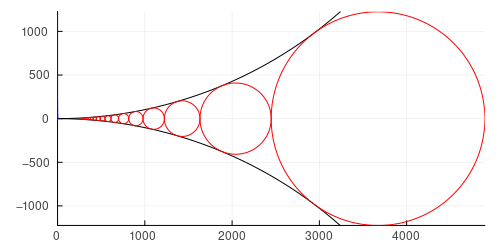
draw(8,9)

   r = 4896.0
   1: x = 280.0, r = 8,  288.0
   2: x = 297.0, r = 9.0,  306.0
   3: x = 316.19999999999624, r = 10.2,  326.4
   4: x = 338.0571428571484, r = 11.657142857142855,  349.71428571428567
   5: x = 363.1648351648321, r = 13.45054945054945,  376.6153846153846
   6: x = 392.3076923076906, r = 15.692307692307693,  408.0
   7: x = 426.545454545461, r = 18.545454545454547,  445.0909090909091
   8: x = 467.3454545454534, r = 22.254545454545465,  489.6000000000001
   9: x = 516.7999999999984, r = 27.200000000000006,  544.0000000000001
   10: x = 578.0, r = 34.00000000000001,  612.0
   11: x = 655.7142857142836, r = 43.71428571428572,  699.4285714285716
   12: x = 757.7142857142878, r = 58.28571428571428,  816.0
   13: x = 897.600000000003, r = 81.6,  979.2
   14: x = 1101.5999999999976, r = 122.4,  1224.0000000000002
   15: x = 1428.0, r = 204.0,  1632.0
   16: x = 2040.0, r = 408.0,  2448.0
   17: x = 3672.0, r = 1224.0,  4896.0
   3.0

draw(99,100)

   r = 7.8804e6
   1: x = 39501.0, r = 99,  39600.0
   2: x = 39700.0, r = 100.0,  39800.0
   3: x = 39901.01522841007, r = 101.01522842639594,  40002.03045685279
   4: x = 40104.07645290719, r = 102.04599606339997,  40206.12244897959
   5: x = 40309.21507052156, r = 103.09262166405024,  40412.307692307695
   6: x = 40516.463124478025, r = 104.1554321966693,  40620.618556701025
   7: x = 40725.853319693466, r = 105.2347631002617,  40831.08808290155
   8: x = 40937.41904142758, r = 106.33095854922276,  41043.74999999999
   9: x = 41151.194371621066, r = 107.44437172774865,  41258.638743455485
        中略
   198: x = 3.283499999999912e6, r = 656699.9999999664,  3.940199999999879e6
   199: x = 5.910299999999696e6, r = 1.9700999999998182e6,  7.880399999999516e6
   3.000000000000123

 

新 macOS

macOS Ventura バージョン 13.0 (22A380)

になったよ！！！(10月25日）

• iPhoneをWebカメラ代わりに使える「連係カメラ」
• 複数のアプリやウィンドウをまとめてグループ化する「ステージマネージャ」
• メールアプリでは、一度送信操作を行なった直後の取り消しや送信予約
• 「FaceTime」がHandoff機能に対応し、MacからiPhoneやiPadへシームレスに通話を引き継げるようになった
• 「Safari」に共有タブグループ機能を追加。ほかのユーザーと閲覧中のタブを共有できる
• WebサイトへのログインにFace IDやTouch IDが利用できる「パスキー」機能を追加(Webサイト側の対応が必要)
• 「メッセージ」アプリでSharePlay連携が可能になったほか、メッセージの編集や送信取り消し、削除したメッセージの復元、未読状態への復元機能などを追加 ]
• 「iCloud」に共有写真ライブラリ機能を追加。5人まで招待でき、個々のライブラリを統合できる
• 「Spotlight」がクイックルックに対応。検索結果の上でスペースキーを押すことでファイルをプレビューできる様になった。また画像検索がWebとローカル、メッセージ、メモ、Finderを横断するようになった
• 一時停止した動画の画面内にあるテキストを認識する機能が日本語と韓国語に対応
• 画像認識が人間に加え新たに動物、鳥、昆虫、彫像、ランドマークを認識するようになった ・ライブキャプションなどアクセシビリティ関連ツールを強化
• iOSに搭載している「天気」「時計」アプリがMacにも追加
• 標的型攻撃を受けた際にシステムをロックダウンする「ロックダウンモード」を追加

 

Python 3.11.0 が出たよ！

Python 3.11.0 がダウンロード可能になった

Python.org からダウンロードしよう

> Python を使って開発や実験を行うときは、用途に応じて専用の実行環境を作成し、切り替えて使用するのが一般的です。

などというフェークニュースには惑わされないで...

まあ，一般ユーザが複数の実行環境なんで必要ないですわ。

R : Nightly builds

運用は自己責任で

R : Nightly builds

Mac は https://mac.r-project.org/

Windows は https://cran.r-project.org/bin/windows/base/R-devel-win.exe

一筋縄では simplify できない式

前の記事で，-2*r1^(3//2)*r2^(3//2)/(r1^2 - 2*r1*r2 + r2^2) + r1*r2*(r1 + r2)/(r1 - r2)^2 が単純には simplify  できないと書いた。

以下のようにすれば，simlify できた。

Windows 11 で RStudio を使うとき...

新しい Windows マシンを使えるようにしているのだがいろいろトラブルが発生する。

その一つに、R の立ち上げにはなんの問題もないのに、RStudio の立ち上げ時に以下の警告メッセージが出るというのに気づいた。オープニングの最初に出るので、狭い R コンソールからはみ出して、気づくのが遅れた。なんてこった。

Warning message:
In normalizePath(path.expand(path), winslash, mustWork) :
  path[1]="C:/Users/user/OneDrive/??????": ファイル名、ディレクトリ名、またはボリューム ラベルの構文が間違っています。

同じのが ４ 連続でしかも赤字で出てくるので、目障りっで仕方ない。しかも、後々ひょっこりまた出たりする。

"C:/Users/user/OneDrive/??????" の "??????" は "ドキュメント" が化けているようだ。

RStudio が使用する環境変数、HOME, R_USER がここを指しているため警告が出るようだ。
R で警告が出ないのは、R はそのような環境変数を使用しないため。

この警告についてインターネットを検索すると、「ユーザ名を日本語でつけているからだよ！」とか「 RStudio（R も）を途中に日本語を含むパスにインストールしたからだよ！」とかある。それはもっともではあるが、それが直接警告メッセージが出る真の原因ではない。
ひどいのになると「C:/Program Files にインストールするのはやめよう！！」とか、とんでもない言いがかりもある。これも、他のディレクトリにインストールしても、警告メッセージが出るという状況は変わらない。

特徴的なのは、多くの海外のユーザも（英語で書かれているので）上のメッセージの解消法を求めて質問や投稿をしているということであり、日本語が真の原因ではないということを示唆しているように思う。

以下に解決法をまとめた。

1. R および RStudio はデフォルトで Program Files にインストールする。

C:/Program Files/R/R-4.2.1
C:/Program Files/RStudio

2. C:/ 直下に（Program Files ディレクトリと同じ階層に）RSTUDIO というディレクトリを作り、更にその中に HOME、R_USER の２つのディレクトリを作成する

3. 環境変数の追加・編集をするが、GUI でやろうとすると、まあ面倒くさい。

「スタート」-->「設定」-->「システムの詳細設定」-->「環境変数」で出てくるウインドウの「システム環境変数」の「新規」で変数名にHOME、「ディレクトリの参照」で C:\RSTUDIO\HOME ディレクトリを選択し「変数値」枠に指定ディレクトリが入ったのを確認して「OK」

R_USER についても同じようにして設定

この記事を書く前に、GUI ではなく、Winows PowerShell で環境変数を設定する方法についてやってみていたが、Windows PowerShell での環境変数の設定は一時的なもののようであり、上述のやり方でなければ恒久的な設定にはならないようだ。注意が必要！！

Windows って、やはり、やだなあ...

 

算額（その2）

算額（その2）

問題2
群馬県高崎市 幸宮神社 文政7年(1824)
https://blog.goo.ne.jp/r-de-r/e/95e0d587bc8ce1d15512697ad8ad6102

下図のように大円，中円，小円がそれぞれ接しており，かつ x 軸にも接している。大円，中円，小円の半径にはどのような関係があるか。

問題は半径　r1，r2，r3 だけを求めているが，図を描くために中円，小円の中心の x 座標 x2，x3 も求める。
なお，大円の中心を (0, r1) とする。

using SymPy

未知数は r1, r2, r3, x2, x3 の 5 個であるが，r1, r2 を与えれば残りの 3 変数が決まる。

@syms r1::positive, r2::positive, r3::positive, x2::positive, x3::positive

   (r1, r2, r3, x2, x3)

大円と中円が接することで，ピタゴラスの定理より，以下の方程式を得る。

eq1 = (r1 - r2)^2 + x2^2 - (r1 + r2)^2
eq1 |> println

   x2^2 + (r1 - r2)^2 - (r1 + r2)^2

x2 について解く。

solve(eq1, x2) |> println

   Sym[2*sqrt(r1)*sqrt(r2)]

中円と小円が接することで，同様にして以下の方程式を得る。

eq2 = (r2 - r3)^2 + (x2 - x3)^2 - (r2 + r3)^2
eq2 |> println

   (r2 - r3)^2 - (r2 + r3)^2 + (x2 - x3)^2

x2 は 2√r1√r2 とわかったので，置き換えて以下の方程式になる。

eq22 = eq2(x2 => 2√r1√r2)
eq22 |> println

   (r2 - r3)^2 - (r2 + r3)^2 + (2*sqrt(r1)*sqrt(r2) - x3)^2

大円と小円について同様に方程式を求める。

eq3 = (r1 - r3)^2 + x3^2 - (r1 + r3)^2
eq3 |> println

   x3^2 + (r1 - r3)^2 - (r1 + r3)^2

連立方程式 eq22, eq3 を x3, r3 について解く。

res = solve([eq22, eq3], (x3, r3));

解は二通り求まる。

3 番目の円が最も小さい場合 と 3 番目の円が最も大きい場合である。後者は，大円，中円，小円の定義から言うと不適切解であるが，一応両方の解を示しておく。

x3, r3 は，かなり長いが r1, r2 のみで表される。

- 第一の解の x3, r3

res[1][1] |> println # x3

   (r1*r2 + (r1 - r2)*(-2*r1^(3/2)*r2^(3/2)/(r1^2 - 2*r1*r2 + r2^2) + r1*r2*(r1 + r2)/(r1 - r2)^2))/(sqrt(r1)*sqrt(r2))

res[1][2] |> println # r3

   -2*r1^(3/2)*r2^(3/2)/(r1^2 - 2*r1*r2 + r2^2) + r1*r2*(r1 + r2)/(r1 - r2)^2

r3 は実は r1*r2/(sqrt(r1) + sqrt(r2))^2 であるが，SymPy では simplify できない。

- 第二の解の x3, r3

res[2][1] |> println # x3

   (r1*r2 + (r1 - r2)*(2*r1^(3/2)*r2^(3/2)/(r1^2 - 2*r1*r2 + r2^2) + r1*r2*(r1 + r2)/(r1 - r2)^2))/(sqrt(r1)*sqrt(r2))

res[2][2] |> println # r3

   2*r1^(3/2)*r2^(3/2)/(r1^2 - 2*r1*r2 + r2^2) + r1*r2*(r1 + r2)/(r1 - r2)^2

r3 は実は r1*r2/(sqrt(r1) - sqrt(r2))^2 であるが，SymPy では simplify できない。

図を描いて，正しいかどうか確かめる。

using Plots

function circle2(ox, oy, r; color=:red)
   theta = 0:0.01:2pi
   x = r.*cos.(theta)
   y = r.*sin.(theta)
   plot!(ox .+ x, oy .+ y, color=color)
end;

function draw(r1, r2)  # r1, r2 を与えれば図を描くことができる
   gr(size=(500, 500), aspectratio=1, label="")
   plot(ylims=(-0.2, 2.3))
   circle2(0, r1, r1, color=:blue)
   # x2 は r1 と r2 だけで決まる
   x2 = 2√r1√r2
   println("x2 = $x2")
   # 3 番目の円が最も小さい場合
   circle2(x2, r2, r2, color=:red)
   x3 = (r1*r2 + (r1 - r2)*(-2*r1^(3/2)*r2^(3/2)/(r1^2 - 2*r1*r2 + r2^2) + r1*r2*(r1 + r2)/(r1 - r2)^2))/(sqrt(r1)*sqrt(r2))
   r3 = -2*r1^(3/2)*r2^(3/2)/(r1^2 - 2*r1*r2 + r2^2) + r1*r2*(r1 + r2)/(r1 - r2)^2
   println("x3 = $x3, r3 = $r3")
   circle2(2√r3, r3, r3, color=:green)
   # 3 番目の円が最も大きい場合（r1 ≧ r2 ≧ r3 という条件をつけるなら，不適解になる）
   x3 = (r1*r2 + (r1 - r2)*(2*r1^(3/2)*r2^(3/2)/(r1^2 - 2*r1*r2 + r2^2) + r1*r2*(r1 + r2)/(r1 - r2)^2))/(sqrt(r1)*sqrt(r2))
   r3 =  2*r1^(3/2)*r2^(3/2)/(r1^2 - 2*r1*r2 + r2^2) + r1*r2*(r1 + r2)/(r1 - r2)^2
   println("x3 = $x3, r3 = $r3")
   circle2(2√r3, r3, r3, color=:brown)
   hline!([0], color=:black)
end;

draw(1, 0.26)

   x2 = 1.019803902718557
   x3 = 0.6754106793494012, r3 = 0.11404489644480492
   x3 = 2.0808160847548067, r3 = 1.0824488946435809

割当問題 Hungarian method / Julia

割当問題　Hungarian method

n 人の人に n 個の仕事を割り当てるとき，最も効率のよい（コストの低い）割当方法を探る。

Project Euler の Problemm 345 で使用する。

Julia では Hungarian パッケージが用意されている。

using Hungarian

普通に使用すると，コストが最小になる割当結果が得られるので，コストを最大にする割当は，行列全体をマイナスにして関数を適用する。得られるコストの絶対値を取ったものが最大コストである。

w = [ 24     1     8
      5     7    14
      6    13    20
     12    19    21
     18    25     2];

assignment, cost = hungarian(w)

   ([2, 1, 0, 0, 3], 8)

w[1,2], w[2,1], w[5, 3] を選ぶのが最適ということだ。

m1 = [  7 53 183 439 863
     497 383 563 79 973
     287  63 343 169 583
     627 343 773 959 943
     767 473 103 699 303
   ];

hungarian(-m1)

   ([5, 2, 3, 4, 1], -3315)

m2 = [7  53 183 439 863 497 383 563  79 973 287  63 343 169 583
   627 343 773 959 943 767 473 103 699 303 957 703 583 639 913
   447 283 463  29  23 487 463 993 119 883 327 493 423 159 743
   217 623   3 399 853 407 103 983  89 463 290 516 212 462 350
   960 376 682 962 300 780 486 502 912 800 250 346 172 812 350
   870 456 192 162 593 473 915  45 989 873 823 965 425 329 803
   973 965 905 919 133 673 665 235 509 613 673 815 165 992 326
   322 148 972 962 286 255 941 541 265 323 925 281 601  95 973
   445 721  11 525 473  65 511 164 138 672  18 428 154 448 848
   414 456 310 312 798 104 566 520 302 248 694 976 430 392 198
   184 829 373 181 631 101 969 613 840 740 778 458 284 760 390
   821 461 843 513  17 901 711 993 293 157 274  94 192 156 574
    34 124   4 878 450 476 712 914 838 669 875 299 823 329 699
   815 559 813 459 522 788 168 586 966 232 308 833 251 631 107
   813 883 451 509 615  77 281 613 459 205 380 274 302  35 805
   ];

@time hungarian(-m2)

     0.000031 seconds (39 allocations: 6.656 KiB)

   ([10, 11, 8, 5, 4, 1, 14, 3, 15, 12, 7, 6, 13, 9, 2], -13938)

13938 が最大コストである。

フィボナッチ数列の10個の和と7番目の数との関係 Julia/SymPy

【C言語】フィボナッチ数列の10個の和と7番目の数との関係
https://sironekolab.com/archives/3021

1.　命題

フィボナッチ数列において，連続する 10 項の和は，第 7 項の 11 倍である。

2.　確認

フィボナッチ数列の生成関数 Fibonacci() を以下のように定義しておく。

function Fibonacci(n)
   x,y = BigInt(0), BigInt(1)
   for i in 1:n
       x,　y = y, x+y
   end
   return x
end;

x = Fibonacci.(13:22)'

   1×10 adjoint(::Vector{BigInt}) with eltype BigInt:
    233  377  610  987  1597  2584  4181  6765  10946  17711

x の和と，x[7] の 11 倍は等しい。

sum(x) # 和

   45991

x[7] * 11 # 7 番目の要素の 11 倍

   45991

SymPy だと簡単に確認できる。

using SymPy
@syms f[1:10]

   (Sym[f₁, f₂, f₃, f₄, f₅, f₆, f₇, f₈, f₉, f₁₀],)

for i in 1:10
   i >= 3 && (f[i] = f[i-2] + f[i-1])
   println("$i: $(f[i])")
end

   1: f₁
   2: f₂
   3: f₁ + f₂
   4: f₁ + 2*f₂
   5: 2*f₁ + 3*f₂
   6: 3*f₁ + 5*f₂
   7: 5*f₁ + 8*f₂
   8: 8*f₁ + 13*f₂
   9: 13*f₁ + 21*f₂
   10: 21*f₁ + 34*f₂

(sum(f), 11(5*f[1] + 8*f[2])) |> println

   (55*f₁ + 88*f₂, 55*f₁ + 88*f₂)

他にも同様な関係式が成り立つことがあるかどうかチェックしてみよう。

次に関係式が成り立つのは n = 14 のときである。

using SymPy
@syms f[1:14]

   (Sym[f₁, f₂, f₃, f₄, f₅, f₆, f₇, f₈, f₉, f₁₀, f₁₁, f₁₂, f₁₃, f₁₄],)

for i in 1:14
   i >= 3 && (f[i] = f[i-2] + f[i-1])
   println("$i: $(f[i])")
end

   1: f₁
   2: f₂
   3: f₁ + f₂
   4: f₁ + 2*f₂
   5: 2*f₁ + 3*f₂
   6: 3*f₁ + 5*f₂
   7: 5*f₁ + 8*f₂
   8: 8*f₁ + 13*f₂
   9: 13*f₁ + 21*f₂
   10: 21*f₁ + 34*f₂
   11: 34*f₁ + 55*f₂
   12: 55*f₁ + 89*f₂
   13: 89*f₁ + 144*f₂
   14: 144*f₁ + 233*f₂

(sum(f), 29(13*f[1] + 21*f[2])) |> println

   (377*f₁ + 609*f₂, 377*f₁ + 609*f₂)

3.　確認の結果

その他にいくつか試してみると，k = 0, 1, 2, 3, ..., とすると n = 4k + 2 のときに関係式が存在する。

   k = 0, n =  2 項の和は      1*f₁ +      1*f₂ で，これは第  3 項   1*f₁ +   1*f₂ の   1 倍である。
   k = 1, n =  6 項の和は      8*f₁ +     12*f₂ で，これは第  5 項   2*f₁ +   3*f₂ の   4 倍である。
   k = 2, n = 10 項の和は     55*f₁ +     88*f₂ で，これは第  7 項   5*f₁ +   8*f₂ の  11 倍である。
   k = 3, n = 14 項の和は    377*f₁ +    609*f₂ で，これは第  9 項  13*f₁ +  21*f₂ の  29 倍である。
   k = 4, n = 18 項の和は   2584*f₁ +   4180*f₂ で，これは第 11 項  34*f₁ +  55*f₂ の  76 倍である。
   k = 5, n = 22 項の和は  17711*f₁ +  28656*f₂ で，これは第 13 項  89*f₁ + 144*f₂ の 199 倍である。
   k = 6, n = 26 項の和は 121393*f₁ + 196417*f₂ で，これは第 15 項 233*f₁ + 377*f₂ の 521 倍である。

OEIS https://oeis.org/?language=japanese も参考にして，各列の数列は以下のように生成される。

4.　関係式の一般項

k 番目の関係式を書き出す関数を定義しておく。

seriese(k) = "k = $k, n = $(4k + 2) 項の和は $(Fibonacci(4k + 2))*f₁ + $(Fibonacci(4k + 3) - 1)*f₂ で，" * 
   "これは第 $(2k+3) 項 $(Fibonacci(2k + 1))*f₁ + $(Fibonacci(2k + 2))*f₂ の $(Fibonacci(2k) + Fibonacci(2k + 2)) 倍である。";

k = 6 まで，更に k = 20 までについて関係式を求める。

for k = 0:20
   println(seriese(k))
end

   k = 0, n = 2 項の和は 1*f₁ + 1*f₂ で，これは第 3 項 1*f₁ + 1*f₂ の 1 倍である。
   k = 1, n = 6 項の和は 8*f₁ + 12*f₂ で，これは第 5 項 2*f₁ + 3*f₂ の 4 倍である。
   k = 2, n = 10 項の和は 55*f₁ + 88*f₂ で，これは第 7 項 5*f₁ + 8*f₂ の 11 倍である。
   k = 3, n = 14 項の和は 377*f₁ + 609*f₂ で，これは第 9 項 13*f₁ + 21*f₂ の 29 倍である。
   k = 4, n = 18 項の和は 2584*f₁ + 4180*f₂ で，これは第 11 項 34*f₁ + 55*f₂ の 76 倍である。
   k = 5, n = 22 項の和は 17711*f₁ + 28656*f₂ で，これは第 13 項 89*f₁ + 144*f₂ の 199 倍である。
   k = 6, n = 26 項の和は 121393*f₁ + 196417*f₂ で，これは第 15 項 233*f₁ + 377*f₂ の 521 倍である。
   k = 7, n = 30 項の和は 832040*f₁ + 1346268*f₂ で，これは第 17 項 610*f₁ + 987*f₂ の 1364 倍である。
   k = 8, n = 34 項の和は 5702887*f₁ + 9227464*f₂ で，これは第 19 項 1597*f₁ + 2584*f₂ の 3571 倍である。
   k = 9, n = 38 項の和は 39088169*f₁ + 63245985*f₂ で，これは第 21 項 4181*f₁ + 6765*f₂ の 9349 倍である。
   k = 10, n = 42 項の和は 267914296*f₁ + 433494436*f₂ で，これは第 23 項 10946*f₁ + 17711*f₂ の 24476 倍である。
   k = 11, n = 46 項の和は 1836311903*f₁ + 2971215072*f₂ で，これは第 25 項 28657*f₁ + 46368*f₂ の 64079 倍である。
   k = 12, n = 50 項の和は 12586269025*f₁ + 20365011073*f₂ で，これは第 27 項 75025*f₁ + 121393*f₂ の 167761 倍である。
   k = 13, n = 54 項の和は 86267571272*f₁ + 139583862444*f₂ で，これは第 29 項 196418*f₁ + 317811*f₂ の 439204 倍である。
   k = 14, n = 58 項の和は 591286729879*f₁ + 956722026040*f₂ で，これは第 31 項 514229*f₁ + 832040*f₂ の 1149851 倍である。
   k = 15, n = 62 項の和は 4052739537881*f₁ + 6557470319841*f₂ で，これは第 33 項 1346269*f₁ + 2178309*f₂ の 3010349 倍である。
   k = 16, n = 66 項の和は 27777890035288*f₁ + 44945570212852*f₂ で，これは第 35 項 3524578*f₁ + 5702887*f₂ の 7881196 倍である。
   k = 17, n = 70 項の和は 190392490709135*f₁ + 308061521170128*f₂ で，これは第 37 項 9227465*f₁ + 14930352*f₂ の 20633239 倍である。
   k = 18, n = 74 項の和は 1304969544928657*f₁ + 2111485077978049*f₂ で，これは第 39 項 24157817*f₁ + 39088169*f₂ の 54018521 倍である。
   k = 19, n = 78 項の和は 8944394323791464*f₁ + 14472334024676220*f₂ で，これは第 41 項 63245986*f₁ + 102334155*f₂ の 141422324 倍である。
   k = 20, n = 82 項の和は 61305790721611591*f₁ + 99194853094755496*f₂ で，これは第 43 項 165580141*f₁ + 267914296*f₂ の 370248451 倍である。

5.　検算

k = 20, n = 82 のとき，第 11 項から第 92　項までのフィボナッチ数列を，n = 82 個の要素を持つベクトルに設定する。

x = Fibonacci.(11:92)

   82-element Vector{BigInt}:
                     89
                    144
                    233
                    377
                    610
                    987
                   1597
                   2584
                   4181
                   6765
                  10946
                  17711
                  28657
                      ⋮
      37889062373143906
      61305790721611591
      99194853094755497
     160500643816367088
     259695496911122585
     420196140727489673
     679891637638612258
    1100087778366101931
    1779979416004714189
    2880067194370816120
    4660046610375530309
    7540113804746346429

x の総和 sum(x) は x[43] の 370248451 倍に等しい。

sum(x), 61305790721611591*x[1] + 99194853094755496*x[2]　# 和, x の型は BigInt

   (19740274219868223023, 19740274219868223023)

x[43], 165580141*x[1] + 267914296*x[2]　# 43 番目の要素

   (53316291173, 53316291173)

370248451 * x[43], 370248451 * (165580141*x[1] + 267914296*x[2]) # 倍数 * 43 番目の要素

   (19740274219868223023, 19740274219868223023)

 

「青チャート式数学II」基本例題141

「青チャート式数学II」基本例題141
https://existence-scholar.com/modules/d3diary/index.php?page=detail&bid=2439&req_uid=1

極座標系でのグラフで悩んでいるようであるが，直交座標系で考えるべきである。（その後解決したようである）
https://existence-scholar.com/modules/d3diary/index.php?page=detail&bid=2440&req_uid=1

問題

0 ≦ θ < 2π で 4*sin(θ)^2 - 4*cos(θ) + 1 の最大値と最小値を求める。

using SymPy, Plots

@syms x, θ, f, g, h, t　# 0 ≦ θ < 2π であるが，ここでは制約をつけないでおく

   (x, θ, f, g, h, t)

1.　素直に原式を微分する

f = 4sin(θ)^2 - 4cos(θ) + 1;

plot(f, projection = :polar, label = "") # 極座標プロット
title!("極座標系でのグラフ", fontfamily="IPAMincho")

g = diff(f); # f の 導関数

plot(f, xlims = (0, 2pi), label = "f")   # 関数
plot!(g, xlims = (0, 2pi), label = "f'") # 導関数
title!("直交座標系でのグラフ", fontfamily="IPAMincho")
hline!([0], label="")

solve(g) |> println # 導関数 = 0 を解く

   Sym[0, -2*pi/3, 2*pi/3]

0 ≦ θ < 2π なので，-2π/3 は 2π - 2π/3 = 4π/3 である。

g(0), f(0) # θ = 0 で最小値 -3

   (0, -3)

g(2pi/3), f(2pi/3) # θ = 2π/3 で最大値 6

   (1.33226762955019e-15, 6.00000000000000)

g(4pi/3), f(4pi/3) # θ = 4π/3 で最大値 6

   (3.10862446895044e-15, 6.00000000000000)

g(pi) = 0 であるが，これは極値である。

g(pi), f(pi) # θ = π で極値 5

   (0, 5)

2.　置換による解

h = f(sin(θ)^2 => 1 - cos(θ)^2) # もとの式を cos(θ) だけを含む式にする
println(h)

   -4*cos(θ)^2 - 4*cos(θ) + 5

i = h(cos(θ) => t) # 更に t = cos(θ) とする
println(i)

   -4*t^2 - 4*t + 5

plot(i, xlims=(-1, 1), label="-4t^2 - 4t + 5")
plot!(diff(i))
hline!([0])

solve(diff(i)) |> println # 導関数が 0 になる t を求める

   Sym[-1/2]

ans1 = solve(cos(θ) + 1//2) # 最大値は t = cos(θ) = -1/2 のとき
println(ans1)

   Sym[2*pi/3, 4*pi/3]

ans2 = solve(cos(θ) - 1) # 最大値は t = cos(θ) = -1/2 のとき
println(ans2)

   Sym[0, 2*pi]

ans1[1], ans1[2], ans2[1]

   (2*pi/3, 4*pi/3, 0)

f(ans1[1]), f(ans1[2]), f(ans2[1])

   (6, 6, -3)

 

大学入試問題を R/caracas で解く

大学入試問題を SymPy で解く を，R の caracas で解いてみる
https://blog.goo.ne.jp/r-de-r/e/e9ae65b5a4f4f53f0f51a9fc1a5ceb5a

library(caracas);

1.　22092501剰余の定理22京都産業大

x = symbol("x")
a = symbol("a")
b = symbol("b")
c = symbol("c")
f = symbol("f")
g = symbol("g")

f = x^11 + 1
g = a*x + b

solve_sys(rbind(subs(g, x, -1L) - subs(f, x, -1L), subs(g, x, 1L) - subs(f, x, 1L)), list(a, b))

   Solution 1:
     a =  1 
     b =  1 

2.　22082401定積分01芝浦工業大

a = symbol("a")
b = symbol("b")
c = symbol("c")
x = symbol("x")
k = symbol("k")
f = symbol("f")

expr = x^3 + a*x^2 +b*x + c

i = int(expr, x, k, k+1)

ans = solve_sys(i - k^3, list(a, b, c))
ans

   Solution 1:
     a =  -3/2 
     b =  1/2 
     c =  0 

f = subs_lst(expr, list(a = ans[[1]]$a, b = ans[[1]]$b, c = ans[[1]]$c))
f

   [caracas]:         2    
               3   3⋅x    x
              x  - ──── + ─
                    2     2

または

f = subs_vec(expr, as_sym(c("a", "b", "c")), unlist(ans))
f

   [caracas]:         2    
               3   3⋅x    x
              x  - ──── + ─
                    2     2

n = symbol("n")
int(f, x, 1, n+1) %>% simplify

   [caracas]:  2 ⎛ 2          ⎞
              n ⋅⎝n  + 2⋅n + 1⎠
              ─────────────────
                      4

sum_(x^3, x, 1, n) %>% simplify

   [caracas]:  2 ⎛ 2          ⎞
              n ⋅⎝n  + 2⋅n + 1⎠
              ─────────────────
                      4

cracas には factor がないので，きれいな形にできない。直接 sympy の factor を呼ぶ。

sympy = get_sympy()

sympy$factor(int(f, x, 1, n+1))

   {pyobj: n**2*(n + 1)**2/4}

sympy$factor(sum_(x^3, x, 1, n))

   '{pyobj: n**2*(n + 1)**2/4}'

n**2*(n + 1)**2/4

   [caracas]:  2        2
              n ⋅(n + 1) 
              ───────────
                   4

 

R で SymPy --- その実態は caracas

caracas: Computer algebra in R

R で SymPy を使うには，rSympPy パッケージというのがあるようなのだが，現在はメンテナンスされていないのか，install.packages() でインストールすることすらできない。

代わりに，caracas というパッケージがある。名前には SymPy を伺わせるものはないが，確かに R から Python の SymPy を使うことになっているようだ。ただ，若干クセがあったり，エクスポートされていない機能があるのが残念だ。

他の　SymPy が使えるならそれを使えばよいが，R しか知らないという場合には caracas を使うのも一法であろう。

1.　インストール

install.packages("caracas")

前提条件として SymPy がインストールされていること。もしインストールされていない場合は以下でインストールできる。

if (!caracas::has_sympy()) {
 caracas::install_sympy() 
}

Python の環境設定

library(reticulate) で Python の環境設定

使ってみよう！！

library(caracas)
sympy_version()

   [1] ‘1.11.1’

x = symbol('x')
eq = 2*x^2 - x
eq

   [caracas]:    2    
              2⋅x  - x

as.character(eq) # 式を文字列に変換する（R へエクスポート）

   '2*x^2 - x'

as_expr(eq) # 式を expression に変換する

   expression(2 * x^2 - x)

tex(eq) # LaTeX にエクスポートする

'2 x^{2} - x'

solve_sys(eq, x) # eq = 0 を x について解く

   Solution 1:
     x =  0 
   Solution 2:
     x =  1/2 

der(eq, x) # eq を x で微分する

   [caracas]: 4⋅x - 1

subs(eq, x, "y") # eq の　x に y を代入

   [caracas]:    2    
              2⋅y  - y

A = matrix(c("x", 2, 0, "2*x"), 2, 2)
B = as_sym(A) # SymPy の行列に変換する
B

   [caracas]: ⎡x   0 ⎤
              ⎢      ⎥
              ⎣2  2⋅x⎦

Binv = inv(B) # 逆行列を求める
Binv

   [caracas]: ⎡ 1      ⎤
              ⎢ ─    0 ⎥
              ⎢ x      ⎥
              ⎢        ⎥
              ⎢-1    1 ⎥
              ⎢───  ───⎥
              ⎢  2  2⋅x⎥
              ⎣ x      ⎦

tex(Binv) # LaTeX 形式で出力する

'\\left[\\begin{matrix}\\frac{1}{x} &amp; 0\\\\- \\frac{1}{x^{2}} &amp; \\frac{1}{2 x}\\end{matrix}\\right]'

上の文字列を LaTeX で出力する。環境により若干の修正が必要になることもある。

$$
\left[\begin{matrix}\frac{1}{x} & 0\\ - \frac{1}{x^{2}} & \frac{1}{2 x}\end{matrix}\right]
$$

eigenval(Binv) # 固有値

   [[1]]
   [[1]]$eigval
   [caracas]: 1
              ─
              x

   [[1]]$eigmult
   [1] 1

   [[2]]
   [[2]]$eigval
   [caracas]:  1 
              ───
              2⋅x

   [[2]]$eigmult
   [1] 1

二乗の和 1 + 2^2 + 3^2 + … + k^2

まずは，SymPy の summation() でやってみる。

using SymPy
@syms n, k
eq = summation(n^2, (n, 1, k)) |> factor

string(eq) # 二乗の和の公式

    "k*(k + 1)*(2*k + 1)/6"

eq(k => 3)

    14

eq(k => 3000000000000000000)

    9000000000000000004500000000000000000500000000000000000

ここまで SymPy
これから Base Julia

f(k) = big(k) * (k + 1) * (2k + 1) // 6 # Base Julia での関数定義

f(3)

    14//1

f(3000000000000000000)

    9000000000000000004500000000000000000500000000000000000//1

big() と // で巨大整数に対応