算額(その142)
三重県四日市市 神明神社 寛政2年
三重県に現存する算額の研究
https://mie-u.repo.nii.ac.jp/?action=repository_uri&item_id=7216&file_id=17&file_no=1
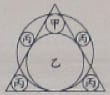
第3問 直角三角形の中に 5 個の円がある。乾円,坤円の直径が与えられているとき,鉤の長さを求めよ。

乾円と坤円の半径を 8, 5 とする。下図のように記号を定め,式を立て,解く。solve() ではなく,nlsolve() による。

using SymPy
@syms r1, r2, r3, x2, x3, r4, r5, x4, x5, x, y;
r4 = 8
r5 = 5
eq1 = (x2 - r1)^2 + (r1 - r2)^2 - (r1 + r2)^2 # 日月
eq2 = (x3 - x2)^2 + (r2 - r3)^2 - (r2 + r3)^2 # 月星
eq3 = (x4 - r1)^2 + (r1 - r4)^2 - (r1 + r4)^2 # 日乾
eq4 = (x2 - x4)^2 + (r2 - r4)^2 - (r2 + r4)^2 # 月乾
eq5 = (x5 - x2)^2 + (r2 - r5)^2 - (r2 + r5)^2 # 月坤
eq6 = (x3 - x5)^2 + (r3 - r5)^2 - (r3 + r5)^2 # 星坤
eq7 = r1*(x + y + sqrt(x^2 + y^2)) - x*y # 直角三角形の面積
eq8 = r1/(x - r1) - r2/(x - x2) # 半径の関係(三角形の相似)
eq9 = r1/(x - r1) - r3/(x - x3); # 半径の関係(三角形の相似)
# res = solve([eq1, eq2, eq3, eq4, eq5, eq6, eq7, eq8, eq9])
println(eq1, ",")
println(eq2, ",")
println(eq3, ",")
println(eq4, ",")
println(eq5, ",")
println(eq6, ",")
println(eq7, ",")
println(eq8, ",")
println(eq9, ",")
(-r1 + x2)^2 + (r1 - r2)^2 - (r1 + r2)^2,
(r2 - r3)^2 - (r2 + r3)^2 + (-x2 + x3)^2,
(-r1 + x4)^2 + (r1 - 8)^2 - (r1 + 8)^2,
(r2 - 8)^2 - (r2 + 8)^2 + (x2 - x4)^2,
(r2 - 5)^2 - (r2 + 5)^2 + (-x2 + x5)^2,
(r3 - 5)^2 - (r3 + 5)^2 + (x3 - x5)^2,
r1*(x + y + sqrt(x^2 + y^2)) - x*y,
r1/(-r1 + x) - r2/(x - x2),
r1/(-r1 + x) - r3/(x - x3),
using NLsolve
function nls(func, params...; ini = [0.0])
if typeof(ini) <: Number
r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]))#, ftol=1e-14)
v = r.zero[1]
else
r = nlsolve((vout, vin)->vout .= func(vin, params...), ini)#, ftol=1e-14)
v = r.zero
end
return v, r.f_converged
end;
function H(u)
(r1, r2, r3, x2, x3, x4, x5, x, y) = u
return [
(-r1 + x2)^2 + (r1 - r2)^2 - (r1 + r2)^2,
(r2 - r3)^2 - (r2 + r3)^2 + (-x2 + x3)^2,
(-r1 + x4)^2 + (r1 - 8)^2 - (r1 + 8)^2,
(r2 - 8)^2 - (r2 + 8)^2 + (x2 - x4)^2,
(r2 - 5)^2 - (r2 + 5)^2 + (-x2 + x5)^2,
(r3 - 5)^2 - (r3 + 5)^2 + (x3 - x5)^2,
r1*(x + y + sqrt(x^2 + y^2)) - x*y,
r1/(-r1 + x) - r2/(x - x2),
r1/(-r1 + x) - r3/(x - x3),
]
end;
iniv = [40.0, 25, 18, 101, 145, 72, 125, 230, 95]
res = nls(H, ini=iniv)
println(res)
([41.038577025077615, 25.64911064067352, 16.030694150420956, 105.92626469082875, 146.4810694819232, 77.27715405015523, 128.57537533150227, 214.0724108004141, 107.59571957603235], true)
勾は 107.59571957603235 であることが分かった。
引用文献に乾円と坤円の直径をm, n としたときに勾の長さを得る式が記載されている。
f(m, n) = 2m*sqrt(m)*(sqrt(m) + sqrt(n))^2/sqrt(n)/(2*sqrt(m*n) - m + n)
f(2*8, 2*5)
107.59571957603244
m,n が整数値のとき,勾が整数になるのは (4, 1), (147, 27), (525, 189), (1134, 224) などとその整数倍のときである。
using Plots
using Printf
function circle(ox, oy, r, color=:red; beginangle=0, endangle=360)
θ = beginangle:0.1:endangle
x = r.*cosd.(θ)
y = r.*sind.(θ)
plot!(ox .+ x, oy .+ y, color=color, linewidth=0.5)
end;
function point(x, y, string="", color=:green, position=:left, vertical=:top; mark=true)
mark && scatter!([x], [y], color=color, markerstrokewidth=0)
annotate!(x, y, text(string, 10, position, color, vertical))
end;
function draw(more)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(r1, r2, r3, x2, x3, x4, x5, x, y) = res[1]
@printf("勾: %.5f\n", y)
plot([0, x, 0, 0], [0, 0, y, 0], color=:black, lw=0.5)
circle(r1, r1, r1)
circle(x2, r2, r2, :blue)
circle(x3, r3, r3, :magenta)
circle(x4, r4, r4, :orange)
circle(x5, r5, r5, :green)
if more == true
point(r1, r1, "日:(r1,r1)", :red, :center, :bottom)
point(x2, r2, "月:(x2,r2)", :blue, :center, :bottom)
point(x3, r3, "星:(x3,r3)", :magenta, :center, :bottom)
point(x4, r4, "乾:(x4,r4)", :orange, :center, :bottom)
point(x5, r5, "坤:(x5,r5)", :green, :center, :bottom)
point(0, y, " y", :black, :left, :bottom)
point(x, 0, " x", :black, :left, :bottom)
hline!([0], color=:black, lw=0.5)
vline!([0], color=:black, lw=0.5)
else
plot!(showaxis=false)
end
end;
draw(false)
勾: 107.59572