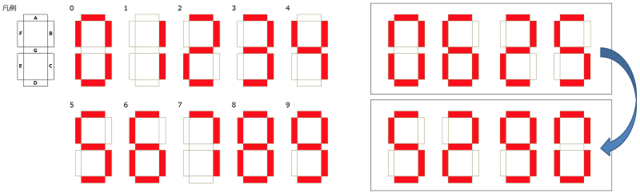
周期表

周期表

締め切りが 2017/04/26 10:00 AM なので，その 1 分後に投稿されるように予約

下図のような表があります。

Y座標(1〜8, L, A)とX座標(1〜18)を与えるので、対応するマスに入る文字列を返すプログラムを書いてください。

【入出力】
入力は
5,6
のように、Y座標とX座標がコンマ区切りで来ます。

出力は、
42
のような感じです。

ただし，
6,3あるいは7,3が入力の場合、表にある通り、LあるいはAを出力してください。
1,8のように、表に文字が書かれていない領域が指定された場合、-を出力してください。

【例】
入力     出力
5,6     42
1,8     -
L,1     57

【補足】
不正な入力に対処する必要はありません。
X座標は 1〜18、Y座標は1〜8, L, A のいずれかです。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

周期表を作るだけなので，以下のようにする。

f = function(s) {
    a = matrix("-", 18, 10)
    a[c(1, 18), 1] = 1:2
    a[c(1:2, 13:18), 2] = c(3:4, 5:10)
    a[c(1:2, 13:18), 3] = c(3:4, 5:10) + 8
    a[1:18, 4:5] = 19:54
    a[1:18, 6:7] = c(55:56, "L", 72:88, "A", 104:118)
    a[1:2, 8] = 119:120
    a[1:15, 9:10] = c(57:71, 89:103)
    s = sub("A", 10, sub("L", 9, s))
    yx = as.integer(unlist(strsplit(s, ",")))
    cat(a[yx[2], yx[1]])
}
f(readLines(file("stdin", "r")))

一行で書くこともできる

a = matrix("-", 18, 10)
a[c(1, 18:20, 31:38, 49:128, 145:159, 163:177)] = c(1:56, "L", 72:88, "A", 104:120, 57:71, 89:103)

全員が楽しめるファミリーレストラン

全員が楽しめるファミリーレストラン

締め切りが 2017/04/25 10:00 AM なので，その 1 分後に投稿されるように予約

設問
大人数でファミリーレストランに行ったとき、複数のテーブルに分かれて座ることにしました。
このとき、1人だけのテーブルを作ることがないように分けます。
例えば、6人の場合、以下の4通りがあります。
・2人＋2人＋2人
・2人＋4人
・3人＋3人
・6人
1つのテーブルに配置できる最大の人数が m 人のとき、
n 人が1つ以上のテーブルに分かれて座る人数のパターンを求めます。
（人数のパターンだけを求め、誰がどのテーブルに座るかは考えないものとします。）
m, n が標準入力からスペース区切りで与えられるとき、
このパターン数を標準出力に出力してください。
なお、m, n は 2≦m≦12、2≦n≦1000 を満たす整数とします。

【入出力サンプル】
標準入力
6 6

標準出力
4

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

この問題は「整数分割」であるが， 2 以上の数で分割するという条件が付く
「オンライン整数列大辞典」にもあるが，m = 12 のような場合には，数列生成法については記述がない
いつものように，m, n の小さいところで解を求めて，行列表示して規則性を探る
個別の m について漸化式を求めようとすると項数が多くなるし，m が大きくなると重回帰分析を応用するという方法では解が求まらなくなる
図をつらつら眺めて，若干の試行錯誤をすると，この行列は以下のように構成できることがわかった



1. n × m 行列を作る（結果的には，1000×12 の行列を作っても，計算時間は微々たるものだとわかるが）
2. m = 2 の列は，n が偶数なら 1，奇数なら 0 なので，a[n, 1] = n %% 2 == 0
3. m = 3 〜 m = 12 の最初の m 個の要素は (0, 1, 1, 2, 2, 4, 4, 7, 8, 12, 14, 21) の先頭から m 個（水色の部分）
4. m 列の m+1 行以降は a[i, m] = a[i, m-1]+a[i-m, m], i >= m+1
 m = 12, n = 30 のとき，a[30, 12] = a[30, 11] + a[18, 12] = 665+81 = 746
 m = 12, n = 987 すなわち，a[987, 12] = 738331156658280 も瞬時に求まる

f = function(m0, n0) {
    tbl = matrix(0, 1000,  12)
    tbl[1:12,] = c(0,1,1,2,2,4,4,7,8,12,14,21)
    tbl[,2] = 0:1
    for (m in 3:12) {
        for (n in (m+1):1000) {
            tbl[n, m] = tbl[n, m-1] + tbl[n-m, m]
        }
    }
    options(scipen=100)
    cat(tbl[n0, m0])
}

f(6, 6) # 4
f(2, 10) # 1
f(5, 20) # 28
f(6, 1000) # 60220121
f(12, 987) # 738331156658280

再帰関数としても書けるが，このままでは実用的ではない

f = function(m, n) {
    if (m == 2) {
        (n %% 2 == 0) + 0
    } else if (n <= m) {
        c(0,1,1,2,2,4,4,7,8,12,14,21)[n]
    } else {
        f(m-1,n)+f(m, n-m)
    }
}

f(7, 11) # 11
f(12, 30) # 746
f(12, 100) # 1312646 かなり時間が掛かる
f(6, 6) # 4
f(2, 10) # 1
f(5, 20) # 28

Re: 日本の高校数学の四分位数の求め方はRの9種類のどれとも違う

http://akiyah.hatenablog.com/entry/2017/04/20/131200

もともとは，

https://twitter.com/f_nisihara/status/847068734665637888?ref_src=twsrc%5Etfw&ref_url=http%3A%2F%2Fakiyah.hatenablog.com%2Fentry%2F2017%2F04%2F20%2F131200

らしいんだけど，このひとも，他人のふんどしで相撲をとっているようで，ちょっと怪しい人だと思うんだけどなあ（^_^）

「高校数学の四分位数の求め方」は間接的ではあるが，http://kou.benesse.co.jp/nigate/math/a13m0403.html が挙げられていて，そこでは，

> データを小さい方から順に並べたとき，中央値に相当するのが「第2四分位数」であり，
> 下位(中央値より小さい方)のデータの中央値が「第1四分位数」
> 上位(中央値より大きい方)のデータの中央値が「第3四分位数」
> となります。

というのを挙げている。確かに四分位数の定義とは違うが，これは，かの有名な「ヒンジ」でしょう。

https://ja.wikipedia.org/wiki/%E5%88%86%E4%BD%8D%E6%95%B0#.E3.83.92.E3.83.B3.E3.82.B8

曰く，

> 四分位数の簡易な求め方として、中央値より上の値の中央値と、中央値より下の値の中央値を使う場合がある。
> この値を特にヒンジ (hinge) と呼び、それぞれ上側ヒンジ・下側ヒンジ、または、第1・第3ヒンジ（第2ヒンジは中央値）と呼ぶ。
> ヒンジは、（厳密に計算した）四分位数とは、中央値から離れる方向に少しだけずれる。データ数が多ければずれは小さくなる。

R で hinge を求めるには，boxplot.stats を使う。

> x = c(33, 34, 55, 57, 60, 61, 61, 2, 3, 5, 6, 7, 8, 12, 15, 18, 20, 27,28, 29, 70)
> median(x[median(x) >= x) # 比較の位置が気持ち悪いのは，このブログの癖を回避するためなので，かんべんな！！！）
[1] 8 # lower hinge
> median(x[x >= median(x)])
[1] 55 # upper hinge
> boxplot.stats(x)
$stats
[1]  2  8 27 55 70  # 2 番目が lower hinge，4 番目が upper hinge
略

> y = c(33, 34, 55, 57, 60, 61, 61, 3, 5, 6, 7, 8, 12, 15, 18, 20, 27, 28, 29, 70)
> median(y[median(y) >= y])
[1] 10 # lower hinge
> median(y[y >= median(y)])
[1] 56 # upper hinge
> boxplot.stats(y)
$stats
[1]  3.0 10.0 27.5 56.0 70.0 # 2 番目が lower hinge，4 番目が upper hinge
略

これが，特殊だって？？？

そんなことはない。

R の boxplot は IQR として，hinge を使っているんだぞ！！！

boxplot(x) を debug してみるとわかるんだけどな。

debug: if (plot) {
    if (is.null(pars$boxfill) && is.null(args$boxfill))
        pars$boxfill = col
    do.call("bxp", c(list(z, notch = notch, width = width, varwidth = varwidth,
        log = log, border = border, pars = pars, outline = outline,
        horizontal = horizontal, add = add, at = at), args[namedargs]))
    invisible(z)
} else z
Browse[3]> z
$stats
     [,1]
[1,]    2
[2,]    8 # これと
[3,]   27
[4,]   55 # これだぞ！！
[5,]   70
以下略

もっとも，高校数学の箱髭図は，この IQR をつかってないというのも読んだ気がするが。

 

境界線の長さ

境界線の長さ

締め切りが 2017/04/19 10:00 AM なので，その 1 分後に投稿されるように予約

【概要】
下図のように、8×8のマス目を白と黒で塗り分けます。
黒と白の境界に線を引きます。
黒い領域の上下左右にある境界線（右図の、赤・緑・青・黄色）の総延長をそれぞれ数えるプログラムを書いてください。
マス目の外側との境界線は数えません。



【入出力】
入力は
f78f447ae68f20af
のように、16進数16桁で来ます。
2桁の16進数が1行を表します。
MSBが左で、1が黒を表します。
上記の入力が、右図に対応します。

出力は、
16,17,11,12
のような感じです。
上下左右の境界線の総延長をコンマ区切りでならべてください。
こちらは10進数です。

【例】
入力             出力
f78f447ae68f20af     16,17,11,12     
ffbc94fc89a34523     10,15,12,13     

【補足】
    不正な入力に対処する必要はありません。

===============================

f = function(s) {
    g = function(s) {
        i = utf8ToInt(s)
        i-48-(i >= 97)*39
    }
    h = function(i) {
        as.integer(rev(c(intToBits(i[2])[1:4], intToBits(i[1])[1:4])))
    }
    s = unlist(strsplit(s, ""))
    a = matrix(sapply(s, g), 2)
    b = matrix(9, 10, 10)
    b[2:9, 2:9] = t(apply(a, 2, h))
    red = green = blue = yellow =0
    for (i in 1:8+1) {
        for (j in 1:8+1) {
            if (b[i, j] == 1) {
                red    = red    + (b[i-1, j] == 0)
                green  = green  + (b[i+1, j] == 0)
                blue   = blue   + (b[i, j-1] == 0)
                yellow = yellow + (b[i, j+1] == 0)
            }
        }
    }
    cat(red, green, blue, yellow, sep=",")
}
f("f78f447ae68f20af") # 16,17,11,12
f("ffbc94fc89a34523") # 10,15,12,13

ダイヤルロックを解除して！

ダイヤルロックを解除して！

締め切りが 2017/04/18 10:00 AM なので，その 1 分後に投稿されるように予約

設問

以下の図のようなダイヤル式のロックが付いたポストがあります。
このロックを解除するには、ダイヤルを左右交互に回転し、特定の m 桁の番号を作るとポストを開けられます。
なお、最初はダイヤルの位置が「0」にセットされているものとし、左回転から開始します。
（番号は「0」以外から始まり、同じ番号が続くことはありません。）　これ重要（見逃して，ドツボに入った）



例えば、m = 3 で「528」という番号の場合、「5」まで左に回し、次に「2」まで右に回し、最後に「8」まで左に回します。
このときに動いた目盛りの数 n を考えます。
上記の「528」の場合、図のように n = 5 + 3 + 6 = 14 となります。
このポストを開けるとき、 m と n は覚えていたのですが、元の番号を忘れてしまいました。
そこで、このポストで m と n の数から番号を推測しようと考えました。
標準入力から m と n がスペース区切りで与えられたとき、考えられる番号が何通りあるかを求め、標準出力に出力してください。
なお、m と n は 0 < m < n < 50 を満たす整数とします。
例えば、 m = 3, n = 6 のとき、以下の10通りがあります。
「104」「178」「180」「192」「202」「214」「290」「312」「324」「434」

【入出力サンプル】
標準入力
3 6

標準出力
10

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

いつも通りの方針に従う。すなわち，m の小さい場合について解を求め，規則性を探る。

f = function(m) {
    distribution = integer(9*m)
    for (i in (10^(m-1)):(10^m - 1)) { # m 桁の数が対象
        s = as.integer(unlist(strsplit(sprintf("%0*d", m+1, i), "")))
        count = 0
        for (k in 1:m) {
            if (s[k] == s[k + 1]) { # 「同じ数字が連続することはない」ことから
                count = 0
                break
            } else if (k%%2 == 1) {
                count = count + (s[k]-s[k + 1]) %% 10 # 左回り
            } else {
                count = count + (s[k + 1]-s[k]) %% 10# 右回り
            }
        }
        if (count != 0) {
            distribution[count] = distribution[count] + 1
        }
    }
    distribution
}

> f(1)
[1] 1 1 1 1 1 1 1 1 1
> f(2)
 [1] 0 1 2 3 4 5 6 7 8 9 8 7 6 5 4 3 2 1
> f(3)
 [1]  0  0  1  3  6 10 15 21 28 36 45 52 57 60 61 60 57 52 45 36 28 21 15 10  6  3  1
> f(4)
 [1]   0   0   0   1   4  10  20  35  56  84 120 165 216 270 324 375 420 456 480 489 480 456 420 375 324 270 216 165
[29] 120  84  56  35  20  10   4   1
> f(5)
 [1]    0    0    0    0    1    5   15   35   70  126  210  330  495  710  976 1290 1645 2030 2430 2826 3195 3510
[23] 3750 3900 3951 3900 3750 3510 3195 2826 2430 2030 1645 1290  976  710  495  330  210  126   70   35   15    5
[45]    1

下図のようになっている。


  以下略
 
m=3 の列は，m=2の列の (1,2,3,4,...,3,2,1) を 1 要素ずつずらして 9 回足す。



この規則をプログラム化して，大きな m, n  のときの解を求める。

f = function(m, n) {
    a = rep(1, 9)
    for (i in 2:m) {
        b = numeric(9*i)
        for (j in 1:9) {
            b[seq_along(a)+j] = b[seq_along(a)+j] + a
        }
        a = b
    }
    a[n]
}

f(3, 6) # 10
f(4, 10) # 84
f(5, 20) # 2826
f(10, 30) # 8337880
f(40, 49) # 1677106600

上下反転した数字表示器

上下反転した数字表示器

締め切りが 2017/04/11 10:00 AM なので，その 1 分後に投稿されるように予約

設問

図のような7セグメントディスプレイを使った数字表示器があります。

この数字表示器を上下逆さに置いたとき、例えば「0625」は「5290」と読むことができます。

逆さに置いたときに対応する数字は以下のようになります。
0 0
1 1
2 2
5 5
6 9
8 8
（「1」は反転すると位置がずれますが、「1」として読み取ることが可能なものとします。）

n 桁を表示できる数字表示器を通常の置き方で置いた時よりも、上下逆さに置いた場合の方が大きな値として読み取ることができるものが何通りあるかを求めるプログラムを作成してください。

例えば、n = 2のとき、以下の21通りがあります。
01, 02, 05, 06, 08, 09, 12, 15, 16, 18, 19, 25, 26, 28, 29, 56, 58, 59, 66, 68, 86

標準入力から自然数 n が与えられますので、パターン数を標準出力に出力してください。
なお、n は最大で20とします。

【入出力サンプル】
標準入力
2

標準出力
21

=============================================

何の策略もないシンプルなプログラムを書いて，n が小さいときの解を求め，既知の数列であるかまたは漸化式を見いだせるかという，いつもの戦略。

f = function(n) {
    d = c(0, 1, 2, 5, 6, 8, 9)
    d.rev = c(0, 1, 2, 5, 9, 8, 6)
    g = function(m) {
        x = x.rev = integer(n)
        n1 = n+1
        for (j in seq_len(n)) {
            k = m %% 7 +1
            x[n1-j] = d[k]
            x.rev[j] = d.rev[k]
            m = m %/% 7
        }
        as.numeric(paste(x.rev, collapse="")) > as.numeric(paste(x, collapse=""))
    }
    count = 0
    for (i in seq_len(7^n)-1) {
        count = count+g(i)
    }
    cat(count, "\n")
}

このプログラムでは，f(7) = 410914 を計算するのに 40 秒近く掛かるが，とにかく

n    f(n)
1    1
2    21
3    154
4    1176
5    8281
6    58653
7    410914

が得られる。

漸化式に用いる項数を2，3，4...（1 項では明らかにむり） として，重回帰モデルを考える

n    x1    x2    x3    x4
1    1     21    154   1176
2    21    154   1176  8281
3    154   1176  8281  58653
4    1176  8281  58653 410914

で，
> a = lm(x4 ~ x1+x2+x3, d)
> summary(a)

Call:
lm(formula = x4 ~ x1 + x2 + x3, data = d)

Residuals:
ALL 4 residuals are 0: no residual degrees of freedom!

Coefficients:
            Estimate Std. Error t value Pr(>|t|)
(Intercept)        0         NA      NA       NA
x1               -49         NA      NA       NA
x2                 7         NA      NA       NA
x3                 7         NA      NA       NA

Residual standard error: NaN on 0 degrees of freedom
Multiple R-squared:      1,    Adjusted R-squared:    NaN
F-statistic:   NaN on 3 and 0 DF,  p-value: NA

> predict(a)
     1      2      3      4
  1176   8281  58653 410914

となり，漸化式，a[1] = 1, a[2] = 21, a[3] = 154 で，n >= 4 は，a[n] = 7*a[n-1] +7*a[n-2]-49*a[n-3]

これに基づいて，

f = function(n) {
    x = numeric(20)
    x[1:3] = c(1, 21, 154)
    if (n >= 4) {
        for (i in 4:n) {
            x[i] = 7*(x[i-1]+x[i-2])-49*x[i-3]
        }
    }
    options(scipen=100)
    cat(x[n])
}
system.time(f(20)) # 39896133007568376    0.001seq.

数学の問題を R で解く（その3）

半径が 1 の互いに外接する 3 つの円に挟まれる部分の面積を求めよ。


解は簡単に求められる
面積 = 「1 辺が 2 の正三角形の面積」 - 「半径 1 の円の面積の半分」

> options(digits=15)
> sqrt(3) - pi/2
[1] 0.161254480773981

R の integrate 関数を使って数値積分を行う



f.a = function(x) 1 - sqrt(1 - x^2)
a = integrate(f.a, 0, sqrt(3) - 1, rel.tol = 1e-14)
f.b = function(x) sqrt(1 - (x - sqrt(3))^2)
b = integrate(function(x) f.a(x)-f.b(x), sqrt(3) - 1, sqrt(3)/2, rel.tol = 1e-14)
2 * (a$value + b$value)

> 2 * (a$value + b$value)
[1] 0.161254480773981

数字の各桁の和と積

数字の各桁の和と積
http://quiz-tairiku.com/q.cgi?mode=view&no=18479

(1) 整数 N の各桁の数の和を新たな整数 N とする，という操作を何度も繰り返す。最初，N=2016^2016 とすると，最終的に 1 桁の整数になるが，その整数は？

library(gmp)
N = as.bigz(2016)^2016
for (i in 1:5) {
    N = sum(as.integer(unlist(strsplit(as.character(N), ""))))
    print(N)
}

答えは 9。
2016 は 9 の倍数（各桁の数字の和が 9 の倍数）。9 の倍数の羃乗は 9 の倍数（各桁の数字の和が 9 の倍数）。よって，各桁の和を取っていけば，いずれは 9 になる。

N = as.bigz(2017)^2017
for (i in 1:5) {
    N = sum(as.integer(unlist(strsplit(as.character(N), ""))))
    print(N)
}

答えは 1 になる。計算せずにわかるかな？

(2) 整数 N の各桁の数の積を新たな整数 N とする，という操作を何度も繰り返す。最初，N=2016^k とすると，最終的に 1 桁の整数になる。但し，k は 2016 以上の整数なら，なんでもよい。その「1 桁の整数になる」と答えた簡単な理由とともに答えよ。

N = as.bigz(2016)^9999
for (i in 1:5) {
    N = prod(as.integer(unlist(strsplit(as.character(N), ""))))
    print(N)
}

答えは 0。
どんな大きな数（？）からスタートしても，各桁には（いずれは） 0 が含まれることが期待される（？？）。だとしたら，各桁の積は 0 以外にあり得ない。
しかし証明は？

クロッシング・ワード

「クロッシング・ワード」問題

締め切りが 2017/04/06 10:00 AM なので，その 1 分後に投稿されるように予約

設問

クロスワードの盤面では、格子状のマス目に白マスまたは黒マスを配置します。

以下は、縦 3 個×横 4 個のマス目に白マス・黒マスを配置する例です。



白マス・黒マスの配置には次のルールがあります。

    黒マスによって白マスの領域が分断されてはならない。
    黒マスが縦・横に連続してはならない。

例えば以下は不適切な配置例です。



自然数 n に対して、縦 3 個 × 横 n 個のマス目に白マス・黒マスを配置する場合の数を F(n) と定義します。

例えば F(1)＝4，F(2)＝11 です。以下に n＝2 の場合の配置の仕方を示します。



同様に、F(3)＝39，F(4)＝121，F(5)＝387 となることが確かめられます。

標準入力から、自然数 n（1 ≦ n ≦ 10^8）が与えられます。
標準出力に F(n) を 10^6 で割った余りを出力するプログラムを書いてください。

===========================

以下のような単純なプログラムを書いて，n が小さいときの解を求める

pentacombinations = function(p) { # 列のパターンの組み合わせ 5^n 通り
    retval = matrix(0, nrow = 5^p, ncol = p)
    for (i in 1:p) {
        retval[, i] = rep(c(rep(0, (5^p/5^i)), rep(1, (5^p/5^i)), rep(2, (5^p/5^i)), rep(3, (5^p/5^i)), rep(4, (5^p/5^i))), length = 5^p)
    }
    retval + 1
}
check = function(x) { # クロスワード配列で，縦横に黒が並んだり，白を黒が分断したりという場合には false，そうでない場合は　true を返す
    n = ncol(x)
    if (ncol(x) > 1) {
        if (x[2, 1] + x[3, 2] == 2 || x[2, 1] + x[1, 2] == 2 ||
            x[2, n] + x[3, n-1] == 2 || x[2, n] + x[1, n-1] == 2) {
            return(FALSE)
        }

        for (j in 1:3) {
            for (i in 2:ncol(x) - 1) {
                if (x[j, i] + x[j, i + 1] == 2)
                    return(FALSE)
            }
        }
        for (i in 2:ncol(x) - 1) {
            if (x[1, i] + x[2, i + 1] + x[3, i] == 3 || x[1, i + 1] + x[2, i] + x[3, i + 1] == 3)
                return(FALSE)
        }
    }
    if (ncol(x) > 2) {
        for (i in 3:ncol(x) - 2) {
            if (x[1, i] + x[2, i + 1] + x[3, i + 2] == 3 || x[1, i + 2] + x[2, i + 1] + x[3, i] == 3)
                return(FALSE)
            if (x[3, i] + x[2, i+1] + x[3, i+2] == 3 || x[1, i] +x[2, i+1] + x[1, i+2] == 3)
                return(FALSE)
        }
    }
    return(TRUE)
}
F = function(n) {
    pattern = matrix(c(0, 0, 0,   0, 0, 1,   0, 1, 0,   1, 0, 0,   1, 0, 1), 3) # 縦方向に黒が続かないパターンは 8 通りのうちの 5 通り
    a = pentacombinations(n)
    b = matrix(0, 3, n)
    count = 0
    for (i in seq_len(nrow(a))) { # クロスワード配列を生成して
        x = b
        for (j in seq_len(n)) {
            x[, j] = pattern[, a[i, j]]
        }
        count = count + check(x) # 妥当なクロスワード配列をカウントする
    }
    count
}

このプログラムにより以下の解を得る
n     F(n)
1     5
2     11
3     39
4     121
5     387
6     1237
7     3955
8     12637
9     40387
10    129069

これ以上の n, F(n) を求めるのは時間が掛かるので，漸化式があるかどうかをチェックする

a1       a2       a3       a4       a5      a6
5        11       39       121      387     1237
11       39       121      387      1237     3955
39       121      387      1237     3955     12637
121      387      1237     3955     12637    40387
387      1237     3955     12637    40387    129069
1237     3955     12637    40387    129069    
3955     12637    40387    129069        
12637    40387    129069            
40387    129069                
129069                    

a1, a2 を使って a3 を求められるか lm(a3 ~ 0+a1+a2)
a1, a2, a3 を使って a4 を求められるか lm(a4 ~ 0+a1+a2+a3)
  :

> a = lm(a6~0+a2+a3+a4+a5, d); summary(a)

Call:
lm(formula = a6 ~ 0 + a2 + a3 + a4 + a5, data = d)

Residuals:
         1          2          3          4          5
-1.245e-12 -1.245e-12 -1.868e-12 -1.245e-12  6.226e-13

Coefficients:
    Estimate Std. Error   t value Pr(>|t|)
a2 2.000e+00  2.590e-12 7.722e+11 8.24e-13
a3 2.000e+00  3.053e-12 6.550e+11 9.72e-13
a4 3.000e+00  3.017e-12 9.945e+11 6.40e-13
a5 2.000e+00  1.109e-12 1.804e+12 3.53e-13

Residual standard error: 2.92e-12 on 1 degrees of freedom
Multiple R-squared:      1,    Adjusted R-squared:      1
F-statistic: 5.413e+32 on 4 and 1 DF,  p-value: < 2.2e-16

> predict(a)

 警告メッセージ:
 summary.lm(a) で:  essentially perfect fit: summary may be unreliable
     1      2      3      4      5
  1237   3955  12637  40387 129069

これで，
a[2] = 11
a[3] = 39
a[4] = 121
a[5] 387
i >= 6 のときは
a[i] = 2*a[i-4]+2*a[i-3]+3*a[i-42]+2*a[i-1]
と予想がつく
なお，F(1) は，上のプログラムの 5 ではなく，実際は　□□□，■□□，□□■，■□■ の4個なんだけど（特別なのかな？？）
以下のプログラムでは F(1) = 3 として，解を求める。

f = function(n) {
    a = integer(n)
    a[1] = 3
    a[2] = 11
    a[3] = 39
    a[4] = 121
    for (i in 5:n) {
        a[i] = (2*(a[i-4]+a[i-3]+a[i-1])+3*a[i-2]) %% 1e6
    }
    cat(a[n])
}

により F(9978) までは制限時間 1 秒以内で求められたが，F(70013454) 時間オーバー
そこで，Java で書いて，すべて OK ということになった。めでたしめでたし。

import java.util.Scanner;

public class crossingWord {

    public static void main(String[] args) {
        if (false) {
            // System.out.println(f(6)); // 1237
            // System.out.println(f(7)); // 3955
            // System.out.println(f(12)); // 318221
            // System.out.println(f(100)); // 193677
            // System.out.println(f(5190)); // 461261
            // System.out.println(f(9978)); // 464781
            // System.out.println(f(70013454)); // 184013
            // System.out.println(f(99999991)); // 885187
        } else {
            Scanner cin = new Scanner(System.in);
            String line;
            line = cin.nextLine();
            int n = Integer.parseInt(line);
            System.out.println(f(n));
        }
    }

    static int f(int n) {
        int a1, a2, a3, a4, a5 = 0, i;
        a1 = 3;
        a2 = 11;
        a3 = 39;
        a4 = 121;
        for (i = 5; n >= i; i++) {
            a5 = (2 * (a1 + a2 + a4) + 3 * a3) % 1000000;
            a1 = a2;
            a2 = a3;
            a3 = a4;
            a4 = a5;
        }
        return a5;
    }

}

プレミアムデー問題

プレミアムデー問題

締め切りが 2017/04/06 10:00 AM なので，その 1 分後に投稿されるように予約

仕様

その月の任意の曜日の最後の日付をプレミアムデーとします。
年月と曜日を表す数値を入力としてうけとり、プレミアムデーをYYYYMMDD形式で出力するプログラムを作成してください。

標準入力

・年, 月, 曜日を表す数値がカンマ区切りで入力されます
・年は4桁の数値です。入力される範囲は 2000-2100 です。
・月は1-2桁の数値です。入力される範囲は 1-12 です。
　例えば1月は1として入力されます。01として入力されることはありません。
・曜日を表す数値は以下の対応関係になっています。

0: 日曜日
1: 月曜日
2: 火曜日
3: 水曜日
4: 木曜日
5: 金曜日
6: 土曜日


例: (2017年3月の金曜日)

2017,3,5

標準出力

・YYYYMMDD 形式で出力する
・MM 月は必ず2桁で0詰して表示する

例（入力の例に対する出力の例）

20170331

その他の仕様

・標準入力の末尾には改行があります
・標準出力の末尾に改行をつけてください
・存在しない日付の入力はありません
・標準入力の仕様で説明した内容以外の入力は行われません（不正入力に対するチェックは不要）

===============================

システムの cal コマンドの出力を利用する

$ cal 11 2017
     11月 2017
日 月 火 水 木 金 土
          1  2  3  4
 5  6  7  8  9 10 11
12 13 14 15 16 17 18
19 20 21 22 23 24 25
26 27 28 29 30

f = function(s) {
    op = options(warn=-1)
    s = as.integer(strsplit(s, ",")[[1]])
    a = system(sprintf("cal %s %s", s[2], s[1]), intern=TRUE)
    a = as.integer(sapply(a, substr, 3*s[3], 3*s[3]+2))
    cat(sprintf("%4d%02d%02d", s[1], s[2], tail(a[!is.na(a)], 1)))
    options(op)
}

f("2017,11,3") # 20171129
f("2017,9,6") # 20170930
f("2016,2,1") # 20160229

幹事が楽な歓送迎会

幹事が楽な歓送迎会

締め切りが 2017/04/04 10:00 AM なので，その 1 分後に投稿されるように予約

設問

人事異動が多く発生する時期になりました。
歓送迎会などの飲み会などを開催したとき、幹事さんの悩みの種となるのがお釣りの準備です。
お釣りが出ないように参加者全員がちょうどの金額を用意してくれると助かるのですが、なかなかうまくいかないものです。

そこで、お釣りが不足しないような順番で会費を集めようと思っています。
例えば、会費が4000円のとき、千円札を出す人が1人いれば、五千円札を出す人が4人いても、
先に千円札の1人から受け付けると、残りの4人のためのお釣りを準備する必要がありません。

ここでは、会費が3000円のとき、千円札を出す人が m 人、五千円札を出す人が n 人いるものとします。
このとき、事前にお釣りを準備しなくても受け付けられる順番が何通りあるかを求めます。
ただし、出すお札の種類での順番についてのみ考え、どの人が出したかは問わないものとします。

例えば、m = 3, n = 2 のとき、以下の5通りがあります。
(1) 千円札 → 千円札 → 千円札 → 五千円札 → 五千円札
(2) 千円札 → 千円札 → 五千円札 → 千円札 → 五千円札
(3) 千円札 → 千円札 → 五千円札 → 五千円札 → 千円札
(4) 千円札 → 五千円札 → 千円札 → 千円札 → 五千円札
(5) 千円札 → 五千円札 → 千円札 → 五千円札 → 千円札

標準入力から参加者数が与えられるとき、m, nのすべての組み合わせについて、
事前にお釣りを準備しなくても受け付けられる順番が何通りあるかを求め、その和を標準出力に出力してください。
なお、参加者は「千円札を出す人」と「五千円札を出す人」のいずれかであるものとし、最大で32人までとします。

例えば、参加者数が5人のとき、m, n の組み合わせと、受け付けられる順番のパターン数は
以下の表のようになるため、12を出力します。

m     n     パターン数
0     5     0通り
1     4     0通り
2     3     2通り
3     2     5通り
4     1     4通り
5     0     1通り
合計       12通り

【入出力サンプル】
標準入力
5

標準出力
12

===================================

千円札と五千円札で支払う人 m 人， n 人とすると，すべての支払い方法は 2^N 通りある。
N = m+n 桁の 2 進数をビット列で表し，そのうちで条件を満たす場合をカウントする。
条件を満たす

f = function(N) {
    bincombinations = function(p) { # library(e1071) # N 桁のビット列
        retval = matrix(0, nrow = 2^p, ncol = p)
        for (n in 1:p) {
            retval[, n] = rep(c(rep(0, (2^p/2^n)), rep(1, (2^p/2^n))), length = 2^p)
        }
        retval
    }

    check = function(x) { # N 桁のビット列
        reservations = 0 # おつりに使える千円札の枚数
        for (i in seq_along(x)) { # ビット列の先端から順にチェック
            if (x[i] == 0) { # 千円札で支払った人
                reservations = reservations + 3 # 千円札が 3 枚殖える
            } else { # 五千円札で支払った人
                if (reservations < 2) { # お釣りに使える千円札が不足
                    return(FALSE)
                }
                reservations = reservations - 2 # お釣りで使うので千円札が 2 枚減る
            }
        }
        return(TRUE) # お釣りで使える千円札が不足することはなかった
    }

    a = bincombinations(N)
    b = apply(a, 1, check)
    n = rowSums(a)
    table(n, b)
}

例えば N=5 のときは
   b
n   FALSE TRUE
  0     0    1
  1     1    4
  2     5    5
  3     8    2
  4     5    0
  5     1    0
成功するのは b=TRUE のときで，n=0 のとき 1 回，n=1 のとき 4 回，n=2 のとき 5 回，n=3 のとき 2 回の，計 1+4+5+2=12 回である。
N=1,2,..., 20 について下図のような数表を作成する。



この数表の規則性は，a[1, 0] = a[2, 0] = a[2,1] = 1 で，a[N, n] = a[N-1, n-1] + a[N-1, n] である。
a[5, 1] = a[4, 0] + a[4, 1] = 1+3 = 4
パスカルの三角形を作る要領である。
ただし，各行で n に制約がある。n = 0.6*N+c(1,0.4, 0.8, 0.2, 0.6)[N %% 5+1] または floor(log10(10*(4^N)))
これを用いてプログラム化する。

f = function(N) {
    a = 1
    if (N >= 2) {
        for (i in 2:N) {
            a = (c(a, 0) + c(0, a))[1:floor(log10(10 * (4^i)))]
        }
    }
    sum(a)
}

> f(5)
[1] 12
> f(7)
[1] 44
> f(18)
[1] 73556
> f(28)
[1] 71886173
> f(32)
[1] 1143455572
> system.time(f(32))
   ユーザ   システム       経過  
     0.019      0.001      0.010