市井の人:「近頃,夏,暑くなっているよねえ。」
知った風の人:「東京都の夏の平均気温は100年で2.4℃上昇している。」
市井の人,あんた,年齢いくつ?物心ついてから三十年として,0.72 ℃くらいしか上がっていない。あんた,そんなに敏感なの?
市井の人:「近頃,夏,暑くなっているよねえ。」
知った風の人:「東京都の夏の平均気温は100年で2.4℃上昇している。」
市井の人,あんた,年齢いくつ?物心ついてから三十年として,0.72 ℃くらいしか上がっていない。あんた,そんなに敏感なの?
雨の多い曜日は月(季節)によっても変わる。
以下は,雨量が 0 でない(少しでも雨の降った)日の割合である(東京)。。
6月の日曜は雨降りの確率が50%!!
df$w
df$month 月 火 水 木 金 土 日
1 23.7 15.3 16.3 13.3 12.4 15.5 14.4
2 19.1 22.5 23.6 22.7 21.3 21.3 21.3
3 37.1 34.0 26.8 30.6 30.6 28.6 33.0
4 35.8 41.5 43.6 39.4 27.7 31.9 29.5
5 32.0 40.8 45.9 44.9 30.9 27.8 35.1
6 38.3 39.4 47.9 44.7 44.2 41.1 50.0
7 34.7 39.8 39.2 46.4 45.4 37.1 34.7
8 39.2 42.3 28.6 26.5 28.6 29.9 25.8
9 45.7 46.8 44.7 40.4 27.7 36.8 42.1
10 43.9 41.8 37.8 34.0 36.1 43.3 39.2
11 45.7 34.0 22.3 27.4 20.0 25.5 27.7
12 20.4 21.6 19.6 20.6 20.6 19.4 17.3
ついでに,晴れの特異日ならぬ,雨の特異日を抽出してみた。
確率が 0.5 より大きいものをピックアップしたところ,6/30 が確率 0.727,6/11, 10/01 がともに確率 0.682 で雨。
301 304 306 411 510 611 612 616 621
63.6 54.5 54.5 59.1 54.5 68.2 54.5 59.1 54.5
623 630 701 703 704 705 706 812 831
59.1 72.7 63.6 54.5 72.7 54.5 54.5 59.1 54.5
904 906 911 916 922 924 930 1001 1006
59.1 59.1 54.5 59.1 54.5 59.1 54.5 68.2 54.5
奥村先生が,「雨の多い曜日」ということで記事を書いておられる。
https://oku.edu.mie-u.ac.jp/~okumura/stat/220517.html
oneway.test() の結果では,曜日ごとの降水量の平均値には差があるとはいえないということだ。
でも,それは「雨の多い曜日」を検討したことになっていないのではないかとちょっと疑問。
降水量が 0 かそうでないかで集計したら以下のようになった。
a
w FALSE TRUE
月 750 398
火 746 402
水 769 379
木 774 374
金 817 331
土 805 343
日 794 354
ちなみに,該当期間では曜日はいずれも 1148 日ずつということだが,%で表示すると
a
w FALSE TRUE
月 65.33101 34.66899
火 64.98258 35.01742
水 66.98606 33.01394
木 67.42160 32.57840
金 71.16725 28.83275
土 70.12195 29.87805
日 69.16376 30.83624
である。月,火,水が多いように見える。

chisq.test() で見てみると,
Pearson's Chi-squared test
data: table(df$V2, df$rain)
X-squared = 17.577, df = 6, p-value = 0.00738
有意ですね。
また,降水量の検定を kraskal.test() でやってみても,
Kruskal-Wallis rank sum test
data: df$V3 by df$V2
Kruskal-Wallis chi-squared = 14.202, df = 6, p-value = 0.02746
有意でした。
まあ,サンプルサイズがべらぼうに多いから有意になりがちかもしれない。
にしても,だったら oneway.test() はどうだったんだということにはなる。
Julia で統計解析--その8 多変量解析
これらの文書群は github で管理することとした
最新バージョン 2022-02-22 07:25
以下を参照のこと
https://r-de-r.github.io/stats/Julia-stats8.html
1. 回帰分析
1.1. 線形最小二乗回帰 Linear Least Square
1.1.1. 単回帰分析
1.1.2. 重回帰分析
1.2. リッジ回帰 Ridge Regression
1.2.1. 説明変数が 1 個の場合
1.2.2. 説明変数が 2 個以上の場合
1.3. GLM パッケージによる回帰分析
1.3.1. 重回帰分析 Ordinary Least Squares Regression
1.3.2. プロビット回帰 Probit Regression
1.3.3. ロジット回帰 Logit Regression
1.4. 多項式回帰
1.4.1. 重回帰プログラムを用いる
1.4.2. 多項式回帰 Polynomials パッケージ
1.5. 指数回帰
1.5.1. 説明変数が 1 個の場合
1.5.2. 説明変数が 2 個以上の場合
1.6. 累乗回帰
1.6.1. 説明変数が 1 個の場合
1.6.2. 説明変数が 2 個以上の場合
1.7. 非線形回帰
2. 判別分析
2.1. 二群判別分析
2.2. 多重判別分析
3. 主成分分析
4. 因子分析
5. 古典的多次元尺度解析
6. クラスター分析
6.1. K-means 法による非階層的クラスター分析
6.2. 階層的クラスター分析
7. カテゴリー変数の取り扱い方
7.1. 重回帰分析
7.2. 判別分析の場合
"""
Julia の Clustering.hclust() は StatsPlots パッケージで普通の(垂直方向の)デンドログラムを描く。機能を持たない。
以下のプログラムは,R の plot() と同じであるが水平方向のデンドログラムを描く。
"""
using Plots
function plot_hclust_horizontal(hc)
function get(i, x)
x[i] < 0 && return(ord[abs(x[i])])
get(x[i], x)
end
n = length(hc.order)
apy = collect(n:-1:1) .+ 0.5
apx = zeros(n)
ord = sortperm(hc.order)
plot(yshowaxis=false, yticks=false, tick_direction=:out, grid=false,
xlims=(-0.05, maximum(hc.height)), ylims=(0, apy[1]),
xlabel="height", label="")
for i in 1:n
annotate!(0, apy[i], text(string(hc.labels[hc.order[i]]) * " ", 8, :right))
end
for i in 1:n-1
c1 = get(i, hc.merge[:,1])
c2 = get(i, hc.merge[:,2])
plot!([apx[c1], hc.height[i], hc.height[i], apx[c2]],
[apy[c1], apy[c1], apy[c2], apy[c2]], color=:black, label="")
apx[c1] = apx[c2] = hc.height[i]
apy[c1] = apy[c2] = (apy[c1] + apy[c2]) / 2
end
plot!()
end
"""
使用法
julia> using RDatasets
julia> iris = RDatasets.dataset("datasets", "iris");
julia> function distancematrix(X)
nr, nc = size(X)
d = zeros(nr, nr)
for i in 1:nr-1
for j in i+1:nr
d[i, j] = d[j, i] = sqrt(sum((X[i, :] .- X[j, :]).^2))
end
end
d
end;
julia> # using Random; Random.seed!(123) # 毎回同じ結果にするためには乱数の種を設定する
using Clustering
julia> x = Matrix(iris[1:20, 1:4]);
julia> D = distancematrix(x);
julia> hc = hclust(D, linkage=:ward);
julia> plot_hclust_horizontal(hc)
"""
これらの文書群は github で管理することとした
最新バージョン 2022-02-12 22:38
以下を参照のこと
https://r-de-r.github.io/stats/Julia-stats3.html
1. データを使用するための準備
1.1. 既存のデータを使用する
1.2. 自前のデータ
2. データフレームの概要
2.1. データフレームの大きさ
2.2. データフレームの変数名
2.3. データフレームの表示
3. データフレームのコピーは copy() で
4. 空データフレーム
5. データフレームの列の参照
6. データフレームの行の参照
7. データフレームの列名の変更
8. 列の抽出
9. 指定された列を削除する
10. 行の抽出
11. 行の削除
12. 重複を除き,ユニークな行のみを含むデータフレームを作る
13. 欠損値を含む行か含まない行か
14. 欠損値を含まない行を抽出する"
15. データフレームの列方向連結
16. データフレームの行方向連結
16.1. cols = :setequal, cols=:orderequal
16.2. cols = :intersect
16.3. cols = :subset
16.4. cols = :union
17. データフレームの最終行の次に 1 行追加する
18. 行を繰り返してデータフレームを作る
19. データフレームに列を挿入する
20. データフレームの要素から新しいデータフレームを作る
21. データフレームの各列に関数を施す
22. ソート(並べ替え)
22.1. ソートされているかをチェックする
22.2. ソートの順番を決める
22.3. 並べ替えベクトルを返す
23. 行の包含
23.1. df1 と df2 のすべての組み合わせを作る crossjoin
23.2. df1 の行のうち,df2 に含まれない行を抽出する antijoin
23.3. df1 に,df2 をマージする innerjoin
23.4. df1 に,df2 をマージする leftjoin
23.5. df1 に,df2 をマージする outerjoin
23.6. df2 に,df1 をマージする rightjoin
23.7. 両方に存在する項目のみでマージする semijoin
24. 欠損値のリストワイズ除去
25. ロングフォーマット(縦長データフレーム)に変換する
26. ワイドフォーマット(横長データフレーム)に変換する
27. データフレームをグループ変数に基づいて分割する
27.1. グループ分けされたデータフレームを抽出する
27.2. グループ化されたデータフレームに関する情報
27.3. 親データフレームを返す
28. 列ごとに関数を適用する
29. 行ごとに関数を適用する
30. クエリーによる操作例
30.1. 要素に関数を適用する @map コマンド
30.2. 条件を満たす行を抽出 @filter コマンド
30.3. データフレームのグループ化 @groupby コマンド
30.4. データのソート @orderby,@orderby_descenidng,@thenby,@thenby_descending コマンド
30.5. データフレームのマージ @groupjoin コマンド
30.6. データフレームの連結 @join コマンド
30.7. キーと値のペアを展開 @mapmany コマンド
30.8. 要素を取り出す @take コマンド
30.9. 要素を捨てる @drop コマンド
30.10. 重複データを除く @unique コマンド
30.11. 列の選択 @select コマンド
30.12. 列名の変更 @rename コマンド
30.13. 変数変換 @mutate コマンド
30.14. 欠損値行を除く @dropna コマンド
30.15. 欠損値を含まないデータフレーム @dissallowna コマンド
30.16. 欠損値の置き換え @replacena コマンド
31. データフレームを二次元配列に変換する
これらの文書群は github で管理することとした
最新バージョン 2022-02-12 22:23
以下を参照のこと
https://r-de-r.github.io/stats/Julia-stats7.html
1. HypothesisTests に含まれる検定関数の使用法
1.1. 検定関数関数の呼び出し方
1.2. 検定関数関数により得られる結果の利用法
2. 検定と推定
2.1. 分布の検定
2.1.1. 観察度数が一様かどうかの検定
2.1.1.1. ピアソンのχ二乗検定
2.1.1.2. 対数尤度比検定(G2 検定)
2.1.2. 観察度数が理論比に從うかどうかの検定
2.1.2.1. ピアソンのχ二乗検定
2.1.2.2. 対数尤度比検定(G2 検定)
2.2. 独立性の検定
2.2.1. ピアソンのχ二乗検定
2.2.2. 対数尤度比検定(G2 検定)
2.3. パワーダイバージェンス検定
2.4. フィッシャーの正確検定
2.5. 二項検定
2.6. t 検定
2.6.1. 一標本の検定(母平均の検定)
2.6.2. 等分散の場合の t 検定
2.6.3. 等分散でない場合 Welch の方法
2.7. マン・ホイットニーの U 検定
2.8. 符号検定
2.9. ウィルコクソンの符号付き順位和検定
2.10. 相関係数の検定
2.11. 対応のない k 標本(独立 k 標本)
2.11.1. 一元元配置分散分析
2.11.2. 一元元配置分散分析(ウェルチの方法)
2.11.3. クラスカル・ウォリス検定
2.12. コルモゴロフ・スミルノフ検定
2.12.1. 1 標本の分布の検定
2.12.2. 2 標本の分布の差の検定
2.13. アンダーソン・ダーリング検定
2.13.1. 1 標本の場合
2.13.2. k 標本の場合
2.14. ワルド・ウォルフォビッツ連検定
2.15. 並べ替え検定(無作為検定)
これらの文書群は github で管理することとした
最新バージョン 2022-02-02 17:05
以下を参照のこと
https://r-de-r.github.io/stats/Julia-stats6.html
1. 数値データの可視化
1.1. ヒストグラム
1.1.1. 一標本の場合
1.3.2. 複数標本の場合
1.4. ボックスプロット(箱ひげ図)
1.5. バイオリンプロット
1.6. ドットプロット
1.7. カーネル密度推定の描画
1.8. Q-Q プロット
1.9. 散布図
1.10. カーネル密度推定
1.11. 散布図行列
これらの文書群は github で管理することとした
最新バージョン 2022-02-02 16:54
以下を参照のこと
https://r-de-r.github.io/stats/Julia-stats5.html
1. 離散データの可視化
1.1. 例示に使用するデータセット
1.1.1. カテゴリーデータ
1.2. 棒グラフ
1.2.1. 一標本の場合
1.2.2. 二標本以上の場合
1.2.2.1. 横に並べる棒グラフ
1.2.2.2. 積み上げ棒グラフ
1.2.3. 複数のグラフを行列状にまとめて表示する方法
1.3. 帯グラフ
1.4. モザイクプロット
1.5. バルーンプロット
これらの文書群は github で管理することとした
最新バージョン 2022-02-02 16:51
以下を参照のこと
https://r-de-r.github.io/stats/Julia-stats4.html
1. 一変量統計
1.1. 一変数の場合
1.1.1. 基礎統計量
1.1.2. パーセンタイル値
1.1.3. 度数分布
1.2. 複数の変数の場合
1.2.1. eachcol() を使う
1.2.2. describe() を使う
1.2.3. combine(), select()/select!(), transform()/transform!() を使う
1.3. グループごとの記述統計量
1.3.1. describe() を使う
1.3.2. 変数ごとに統計量を一覧表示
2. 二変量統計
2.1. 二重クロス集計表
2.2. 相関係数,共分散
2.2.1. 欠損値を含まない場合
2.2.1.1. それぞれの関数を使う
2.2.1.2. combine() を使う
2.2.2. 欠損値を含む場合
2.2.2.1. それぞれの関数を使う
2.2.2.2. combine() を使う
2.3. 相関係数行列,分散・共分散行列
2.3.1. 欠損値を含まない場合
2.3.2. 欠損値を含む場合
3. 多変量統計
3.1. 多重クロス集計表
これらの文書群は github で管理することとした
最新バージョン 2022-02-02 16:45
以下を参照のこと
https://r-de-r.github.io/stats/Julia-stats2.html
1. データをデータフレームへ読み込む
1.1. Excel のワークシートファイル
1.2. CSV ファイル
1.2.1. 典型的な CSV ファイル
1.2.2. 一般の CSV ファイル
1.2.3. CSV.read の引数
1.3. インターネット上の CSV ファイル
1.4. モニター上に表示された表をデータフレームに読み込む
1.5. クリップボードにコピーした内容をデータフレームにする
1.6. 文字列行から入力する
1.7. エンコーディングの違うファイルを読む
1.8. デリミタで区切られていない固定書式ファイルを読む
2. データフレームを CSV ファイルに書き出す
2.1. CSV.write の引数
これらの文書群は github で管理することとした
最新バージョン 2022-01-26 22:55
以下を参照のこと
https://r-de-r.github.io/stats/Julia-stats1.html
1. Julia を使ってみる
1.1. 必要なファイルをダウンロードする
1.2. Julia のインストール
1.3. Julia を起動し終了する
1.4. 作業ディレクトリを変える
1.5. Julia の環境設定をする
1.5.1. startup.jl ファイルがあるかを確認
1.5.2. config がなかった場合
1.5.3. startup.jl がある場合
1.5.4. 変更内容の確認
1.6. オンラインヘルプを使う
1.7. パッケージを利用する
1.8. エディタを使う
1.8.1. Atom
1.8.2. Jupyter lab
1.9. 結果を保存する
Anscombe データセットは,記述統計学においてときどき言及されるものである。
4 組のデータ (x1, y1), (x2, y2), (x3, y3), (x4, y4) は,それぞれの変数の平均値,分散,二変数間の共分散,したがって相関係数も全て同じというものである。
# x1 x2 x3 x4 y1 y2 y3 y4
data = [
10 10 10 8 8.04 9.14 7.46 6.58
8 8 8 8 6.95 8.14 6.77 5.76
13 13 13 8 7.58 8.74 12.7 7.71
9 9 9 8 8.81 8.77 7.11 8.84
11 11 11 8 8.33 9.26 7.81 8.47
14 14 14 8 9.96 8.1 8.84 7.04
6 6 6 8 7.24 6.13 6.08 5.25
4 4 4 19 4.26 3.1 5.39 12.5
12 12 12 8 10.8 9.13 8.15 5.56
7 7 7 8 4.82 7.26 6.42 7.91
5 5 5 8 5.68 4.74 5.73 6.89
];
using DataFrames
df = DataFrame(data, [:x1, :x2, :x3, :x4, :y1, :y2, :y3, :y4])
using Statistics
[println("mean(x$i) = $(mean(df[:, i])), mean(y$i) = $(mean(df[:, 4+i]))") for i in 1:4];
[println("var(x$i) = $(var(df[:, i])), var(y$i) = $(var(df[:, 4+i]))") for i in 1:4];
[println("cov(x$i, y$i) = $(cov(df[:, i], df[:, 4+i])), cor(x$i, y$i) = $(cor(df[:, i], df[:, 4+i]))") for i in 1:4];
mean(x1) = 9.0, mean(y1) = 7.497272727272727
mean(x2) = 9.0, mean(y2) = 7.500909090909091
mean(x3) = 9.0, mean(y3) = 7.496363636363637
mean(x4) = 9.0, mean(y4) = 7.50090909090909
var(x1) = 11.0, var(y1) = 4.100701818181819
var(x2) = 11.0, var(y2) = 4.127629090909091
var(x3) = 11.0, var(y3) = 4.080845454545455
var(x4) = 11.0, var(y4) = 4.12324909090909
cov(x1, y1) = 5.489, cor(x1, y1) = 0.8172742068397078
cov(x2, y2) = 5.5, cor(x2, y2) = 0.8162365060002429
cov(x3, y3) = 5.481, cor(x3, y3) = 0.8180660798450472
cov(x4, y4) = 5.499, cor(x4, y4) = 0.8165214368885028
よく使われる統計量で見分けが付かなくても,これらを散布図で見れば,明らかな違いがある(fig1, fig2, fig3, fig4)。図に示した直線は回帰直線である。
using Plots
pyplot(grid=false, label="", xlabel="x", ylabel="y")
plt1 = scatter(df.x1, df.y1, smooth=true, title="fig1");
plt2 = scatter(df.x2, df.y2, smooth=true, title="fig2");
plt3 = scatter(df.x3, df.y3, smooth=true, title="fig3");
plt4 = scatter(df.x4, df.y4, smooth=true, title="fig4");
plt5 = scatter(df.y4, df.x4, smooth=true, xlabel="y", ylabel="x", title="fig5");
plot(plt1, plt2, plt3, plt4, plt5)

統計図の重要性を説くためのうってつけのデータセットである。
違いは確かにあるが,その先はどうするのかについてはあまり言及がない。予測という観点からデータを見てみよう。
using GLM
df.x_power2 = df.x1 .^ 2
result2 = lm(@formula(y2 ~ x2 + x_power2), df)
StatsModels.DataFrameRegressionModel{LinearModel{LmResp{Vector{Float64}}, DensePredChol{Float64, LinearAlgebra.Cholesky{Float64, Matrix{Float64}}}}, Matrix{Float64}}
Formula: y2 ~ 1 + x2 + x_power2
Coefficients:
──────────────────────────────────────────────────────
Estimate Std.Error t value Pr(>|t|)
──────────────────────────────────────────────────────
(Intercept) -5.99573 0.00432995 -1384.71 <1e-22
x2 2.78084 0.00104006 2673.74 <1e-24
x_power2 -0.126713 5.70977e-5 -2219.24 <1e-23
──────────────────────────────────────────────────────
予測値は完全に当てはまる。
scatter(df.x2, df.y2)
o = sortperm(df.x2)
xval = minimum(df.x2):0.05:maximum(df.x2)
predict2 = coef(result2)[1] .+ coef(result2)[2] .* xval + coef(result2)[3] .* xval .^2
plot!(xval, predict2)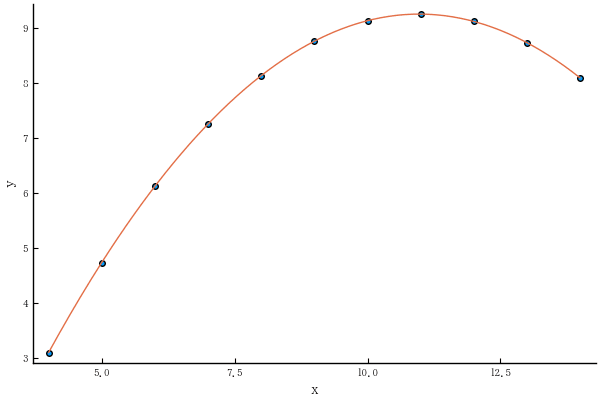
df.x3_dummy = df.x3 .== 13
result3 = lm(@formula(y3 ~ x3 + x3_dummy), df)
StatsModels.DataFrameRegressionModel{LinearModel{LmResp{Vector{Float64}}, DensePredChol{Float64, LinearAlgebra.Cholesky{Float64, Matrix{Float64}}}}, Matrix{Float64}}
Formula: y3 ~ 1 + x3 + x3_dummy
Coefficients:
─────────────────────────────────────────────────────
Estimate Std.Error t value Pr(>|t|)
─────────────────────────────────────────────────────
(Intercept) 4.00565 0.00292424 1369.81 <1e-22
x3 0.34539 0.000320591 1077.35 <1e-21
x3_dummy 4.20429 0.0035265 1192.2 <1e-21
─────────────────────────────────────────────────────
予測値は完全に当てはまる。
scatter(df.x3, df.y3)
o = sortperm(df.x3)
plot!(df.x3[o], predict(result3)[o])
fig4 の x座標,y座標を入れ替えたものが fig5 である。回帰直線に当てはめるとどちらも同じようであるが,fig5 にロジスティック曲線を当てはめてみよう。
すなわち,図(データ)の解釈として,「従属変数 x は二値データ。独立変数 y が小さい内は反応がない(x=8)が,yが大きくなると反応が現れる(x = 19)」と考える。
なお,このままだと当てはめができないので,一点だけ変更する(下図の上に2点ある左の方)。
df.x4p = df.y4 .> 10
df.x4p[5] = 1
result4 = glm(@formula(x4p ~ y4), df, Binomial())
StatsModels.DataFrameRegressionModel{GeneralizedLinearModel{GlmResp{Vector{Float64}, Binomial{Float64}, LogitLink}, DensePredChol{Float64, LinearAlgebra.Cholesky{Float64, Matrix{Float64}}}}, Matrix{Float64}}
Formula: x4p ~ 1 + y4
Coefficients:
─────────────────────────────────────────────────────
Estimate Std.Error z value Pr(>|z|)
─────────────────────────────────────────────────────
(Intercept) -19.574 18.437 -1.06167 0.2884
y4 2.20803 2.20089 1.00324 0.3157
─────────────────────────────────────────────────────
予測曲線を描いてみるともっともらしく見えるようになる。
scatter(df.y4, df.x4p)
xval = minimum(df.y4):0.05:maximum(df.y4)
predict4 = 1 ./ (1 .+ exp.(-coef(result4)[1] .- coef(result4)[2] .* xval))
plot!(xval, predict4)
以上のように,データの姿形,理論的背景をよく考えてモデルを構築する必要があるということだ。
https://nazesuugaku.com/santaclausinai/
> サンタクロースがいないことを証明するために、サンタクロースの条件を定義したいと思います。
> サンタクロースは世界に1人しかいない
この条件は誰もが認めるものではない(誰も証明できない,あるいはその反証がないならな)ので,前提条件が否定されれば,当然のことながらあとは,全てなりたちません。
全世界のよい子たち,サンタクロースはいますよ。
=====
サンタクロースがいないことを証明してやるよwww
https://sekayume.com/?p=2456
サンタがいないことを物理的に証明する動画
https://www.youtube.com/watch?v=-uTGB-D0PQ4
世の中には,ヒドイ人間がある程度はいますね。