算額（その600）

算額（その600）

長崎市 鎮西大社諏訪神社 明治20年(1887)
米光丁: 長崎県の和算の概説
http://hyonemitsu.web.fc2.com/Nagasakiwasan.pdf

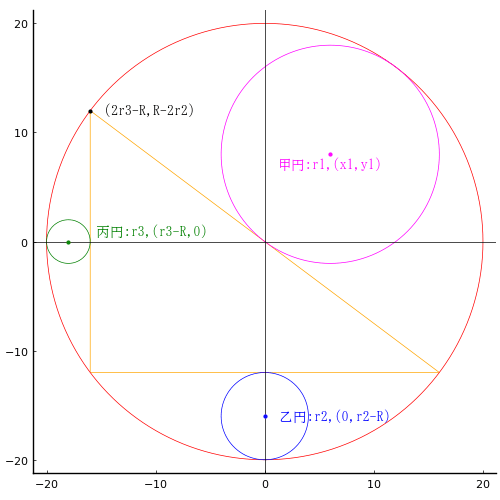
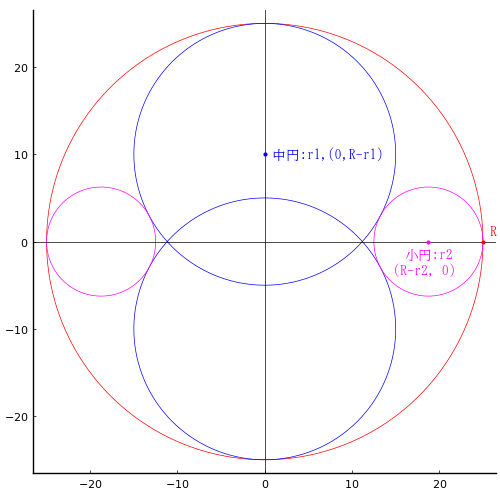
問題 13. 外円の中に大円，中円，小円を入れる。大円の直径が 36 寸のとき，小円の直径はいかほどか。

外円の半径と中心座標を R, (0, 0)
大円の半径と中心座標を r1, (0, r1 - R)
中円の半径と中心座標を r2, (0, R - r2)
小円の半径と中心座標を r3, x3, y3)
斜線と外円の交点座標を (x, -sqrt(R^2 - x^2))
とおき，以下の連立方程式を解く。

include("julia-source.txt");

using SymPy

@syms x::positive, R::positive, r1::positive, r2::positive, r3::positive, x3::positive, y3::positive
eq1 = r1 + r2 - R
eq2 =x3^2 + (y3 - R + r2)^2 - (r2 - r3)^2
eq3 = (y3 - R + r2)/x3*(-R -sqrt(R^2 - x^2))/x + 1
eq4 = (r2 - 2r3)/(R - r2) - x/sqrt(x^2 +(sqrt(R^2 - x^2) + R)^2)
eq5 = distance(0, R, x, -sqrt(R^2 - x^2), x3, y3) - r3^2
eq6 = distance(0, R, x, -sqrt(R^2 - x^2), 0, r1 - R) - r1^2;
# solve([eq1, eq2, eq3, eq4, eq5, eq6], (x, R, r2, r3, x3, y3))

using NLsolve

function nls(func, params...; ini = [0.0])
   if typeof(ini) <: Number
       r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=big"1e-40")
       v = r.zero[1]
   else
       r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=big"1e-40")
       v = r.zero
   end
   return v, r.f_converged
end;

function H(u)
   (x, R, r2, r3, x3, y3) = u
   return [
       -R + r1 + r2,  # eq1
       x3^2 - (r2 - r3)^2 + (-R + r2 + y3)^2,  # eq2
       1 + (-R - sqrt(R^2 - x^2))*(-R + r2 + y3)/(x*x3),  # eq3
       -x/sqrt(x^2 + (R + sqrt(R^2 - x^2))^2) + (r2 - 2*r3)/(R - r2),  # eq4
       -r3^2 + (x3 - x*(R^2 - R*y3 + R*sqrt(R^2 - x^2) + x*x3 - y3*sqrt(R^2 - x^2))/(2*R*(R + sqrt(R^2 - x^2))))^2 + (y3 - (R^2 + R*y3 - R*sqrt(R^2 - x^2) - x*x3 + y3*sqrt(R^2 - x^2))/(2*R))^2,  # eq5
       -r1^2 + (-x + r1*x/(2*R))^2 + (-R + r1 - (R^2 - (R + sqrt(R^2 - x^2))*(2*R - r1)/2)/R)^2,  # eq6
   ]
end;

r1 = 36//2
iniv = BigFloat[22, 35, 17, 5, 10, 20]
res = nls(H, ini=iniv)

   (BigFloat[22.62741699796952078082701958735516925711475000603116912031953235176946800128799, 36.00000000000000000000000000000000000000000000000000023997217352842064306535952, 18.0000000000000000000000000000000000000000000000000002399721735284206430653598, 6.000000000000000000000000000000000000000000000000000298124281531485670596315888, 11.3137084989847603904135097936775846285573750030155858282654603937949442060392, 22.00000000000000000000000000000000000000000000000000175488066987747432400063655], true)

小円の直径は 12 寸である。

その他のパラメータは以下の通り。
x = 22.6274;  R = 36;  r2 = 18;  r3 = 6;  x3 = 11.3137;  y3 = 22

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r1 = 36//2
   (x, R, r2, r3, x3, y3) = res[1]
   @printf("小円の直径 = %g;  x = %g;  R = %g;  r2 = %g;  r3 = %g;  x3 = %g;  y3 = %g\n", 2r3, x, R, r2, r3, x3, y3)
   plot()
   circle(0, 0, R, :blue)
   circle(0, r1 - R, r1, :green)
   circle(0, R - r2, r2, :orange)
   circle(x3, y3, r3)
   segment(0, R, x, -sqrt(R^2 - x^2))
   segment(0, R, -x, -sqrt(R^2 - x^2))
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
       point(0, R - r2, " R-r2")
       point(x3, y3, "(x3,y3)")
   end
end;

算額（その599）

算額（その599）

 

七六 北埼玉郡騎西町中種足 雷神社 明治5年(1872)
埼玉県立図書館：埼玉県史料集 第二集『埼玉の算額』，昭和44年，誠美堂印刷所，埼玉県与野市.

埼玉の算額ほか
https://gunmawasan.web.fc2.com/files/saitama-sangaku-h24.html
愛宕神社の復元算額　明治１３年（部分拡大図）（加須市）
https://gunmawasan.web.fc2.com/files/sangak-corner/atago-3s.jpg

東京都中央区 福徳神社 令和2年(2020)
http://www.wasan.jp/tokyo/hukutoku1.html

正三角形を 2 本の線で 4 つの部分に分け，その中に大小の円をそれぞれ 2 個入れる。大円の直径が 1 のとき，小円の直径はいくらか。

正三角形の一辺の長さを 2a とする。
線分と斜辺の交点座標を (±x, (a - x)√3) とする。
大円の半径と中心座標を r1, (0, y1), (0, r1)
小円の半径と中心座標を r2, (x2, y2)
とおき，以下の連立方程式を解く。

include("julia-source.txt");

using SymPy

@syms a::positive, x::positive,
     r1::positive, x1::positive, y1::positive,
     r2::positive, x2::positive, y2::positive

eq1 = distance(0, sqrt(Sym(3))a, a, 0, 0, y1) - r1^2
eq2 = distance(0, sqrt(Sym(3))a, a, 0, x2, y2) - r2^2
eq3 = distance(-x, (a-x)sqrt(Sym(3)), a, 0, 0, y1) - r1^2
eq4 = distance(-x, (a-x)sqrt(Sym(3)), a, 0, x2, y2) - r2^2
eq5 = distance(x, (a-x)sqrt(Sym(3)), -a, 0, 0, r1) - r1^2
eq6 = distance(x, (a-x)sqrt(Sym(3)), -a, 0, x2, y2) - r2^2;
# solve([eq1, eq2, eq3, eq4, eq5, eq6])

using NLsolve

function nls(func, params...; ini = [0.0])
   if typeof(ini) <: Number
       r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=big"1e-40")
       v = r.zero[1]
   else
       r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=big"1e-40")
       v = r.zero
   end
   return v, r.f_converged
end;

function H(u)
   (a, x, y1, r2, x2, y2) = u
   return [
3*a^2/4 - sqrt(3)*a*y1/2 - r1^2 + y1^2/4,  # eq1
-r2^2 + (-3*a + 3*x2 + sqrt(3)*y2)^2/16 + (-sqrt(3)*a + sqrt(3)*x2 + y2)^2/16,  # eq2
(3*a^4/4 - 3*a^3*x/2 - sqrt(3)*a^3*y1/2 - a^2*r1^2 + 3*a^2*x^2/4 + a^2*y1^2/4 + a*r1^2*x + sqrt(3)*a*x^2*y1/2 + a*x*y1^2/2 - r1^2*x^2 + x^2*y1^2/4)/(a^2 - a*x + x^2),  # eq3
-r2^2 + (a + x)^2*(-sqrt(3)*a^2 + sqrt(3)*a*x + sqrt(3)*a*x2 + a*y2 - sqrt(3)*x*x2 + x*y2)^2/(16*(a^2 - a*x + x^2)^2) + (-3*a^3 + 6*a^2*x + 3*a^2*x2 + sqrt(3)*a^2*y2 - 3*a*x^2 - 6*a*x*x2 + 3*x^2*x2 - sqrt(3)*x^2*y2)^2/(16*(a^2 - a*x + x^2)^2),  # eq4
(3*a^4 - 2*sqrt(3)*a^3*r1 - 6*a^3*x - 3*a^2*r1^2 + 3*a^2*x^2 + 6*a*r1^2*x + 2*sqrt(3)*a*r1*x^2 - 3*r1^2*x^2)/(4*(a^2 - a*x + x^2)),  # eq5
-r2^2 + (-sqrt(3)*a^3 - sqrt(3)*a^2*x2 + a^2*y2 + sqrt(3)*a*x^2 + 2*a*x*y2 + sqrt(3)*x^2*x2 + x^2*y2)^2/(16*(a^2 - a*x + x^2)^2) + (3*a^3 - 6*a^2*x + 3*a^2*x2 - sqrt(3)*a^2*y2 + 3*a*x^2 - 6*a*x*x2 + 3*x^2*x2 + sqrt(3)*x^2*y2)^2/(16*(a^2 - a*x + x^2)^2),  # eq6
   ]
end;

r1 = 1/2
iniv = BigFloat[1.6, 0.66, 1.74, 0.322, 0.56, 1.1] .* (2r1)
res = nls(H, ini=iniv)

   (BigFloat[1.573132184970985912579820468331052169654464272601005512809483077205430728737341, 0.6610365985079724914150555424853615260166663839137217848002503187911426334707547, 1.724744871391588873493812097618873490781894353477567544930381227134074172251389, 0.3224744871391588398986467839454922576529915481447599591870862696864391756755701, 0.5585421958697395716072717462463142074739205600259983862524414059477805245308117, 1.112372435695794479712354981538013592707116186365025213663076513709077532563648], true)

大円の直径が 1 のとき，小円の直径は 0.644949 である。

その他のパラメータは以下の通り。
小円の直径 = 0.644949;  r1 = 0.5;  a = 1.57313;  x = 0.661037;  y1 = 1.72474;  r2 = 0.322474;  x2 = 0.558542;  y2 = 1.11237

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r1 = 1/2
   (a, x, y1, r2, x2, y2) = res[1]
   @printf("小円の直径 = %g;  r1 = %g;  a = %g;  x = %g;  y1 = %g;  r2 = %g;  x2 = %g;  y2 = %g\n", 2r2, r1, a, x, y1, r2, x2, y2)
   plot([a, 0, -a, a], [0, √3a, 0, 0], color=:magenta, lw=0.5)
   circle(0, y1, r1)
   circle(0, r1, r1)
   circle(x2, y2, r2, :blue)
   circle(-x2, y2, r2, :blue)
   segment(-a, 0, x, (a - x)√3)
   segment(a, 0, -x, (a - x)√3)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
       point(0, y1, " 大円:r1\n (0,y1)", :red, :left, :vcenter)
       point(0, r1, " 大円:r1\n (0,r1)", :red, :left, :vcenter)
       point(x2, y2, "小円:r2\n(x2,y2)", :blue, :center, delta=-delta)
       point(a, 0, "a", :magenta, :left, :bottom, delta=delta/2)
       point(0, √3a, " √3a", :magenta, :left, :vcenter)
       point(x, √3(a-x), " (x,√3(a-x))", :magenta, :left, :vcenter)
   end
end;

算額（その598）

算額（その598）

八五 北葛飾郡三郷町上彦川戸 香取神社 明治13年(1880)
埼玉県立図書館：埼玉県史料集 第二集『埼玉の算額』，昭和44年，誠美堂印刷所，埼玉県与野市.

東京都中央区 福徳神社 令和2年(2020)
http://www.wasan.jp/tokyo/hukutoku1.html

高さ 30，底辺 42 の直角三角形を 2 本の線分で分け，面積を 3 等分する。このとき長い方の線分の長さはいくらか。

2 本の線分と斜辺の交点座標を (x1, y1), (x2, y2)，高さを「鈎」，底辺を「股」とおく。

弦を底辺として考えると，赤，白，緑の三角形の高さは同じなので，面積がおなじになるためには弦は三等分しなければならない。
そうすれば，
x1,y1 は 42*(2/3), 30*(1/3) で 28, 10
x2,y2 は 42*(1/3), 30*(2/3) で 14, 20
と暗算でわかる。
線分の長さは暗算ではわからないが。√(28^2 + 10^2) と √(14^2 + 20^2) の長いほうが答え 29.732137494637012 である。

√(28^2 + 10^2), √(14^2 + 20^2) 

   (29.732137494637012, 24.413111231467404)

連立方程式を解くなら，以下のように。

include("julia-source.txt");

using SymPy

@syms 鈎::positive, 股::positive, x1::positive, y1::positive,
     x2::positive, y2::positive

S = 股*鈎/2
eq1 = 股*y1/2 - S/3
eq2 = 鈎*x2/2 - S/3
eq3 = y1/(股 - x1) - 鈎/股
eq4 = (鈎 - y2)/x2 - 鈎/股
(x1, y1, x2, y2) = solve([eq1, eq2, eq3, eq4], (x1, y1, x2, y2))

   Dict{Any, Any} with 4 entries:
     x1 => 2*股/3
     y1 => 鈎/3
     x2 => 股/3
     y2 => 2*鈎/3

(鈎, 股) = (30, 42)

   (30, 42)

(x1, y1) = (2*股/3, 鈎/3)

   (28.0, 10.0)

(x2, y2) = (股/3, 2*鈎/3)

   (14.0, 20.0)

(緑の面積, 赤の面積, 白の面積) = (股*y1/2, 鈎*x2/2, 股*鈎/2 - 股*y1/2 - 鈎*x2/2)

   (210.0, 210.0, 210.0)

線分の長さ =  (sqrt(x1^2 + y1^2), sqrt(x2^2 + y2^2))

   (29.732137494637012, 24.413111231467404)

長い方の線分の長さ = maximum(線分の長さ)

   29.732137494637012

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   @printf("(x1, y1) = (%g, %g);  (x2, y2) = (%g, %g)\n", x1, y1, x2, y2)
   plot([0, 股, 0, 0], [0, 0, 鈎, 0], color=:black, lw=0.5)
   plot!([0, 股, x1, 0],  [0, 0, y1, 0], color=:green, lw=0.5, seriestype=:shape, fillcolor=:green)
   plot!([0, x2, 0, 0], [0, y2, 鈎, 0], color=:red, lw=0.5, seriestype=:shape, fillcolor=:red)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
       point(x1, y1, "　(x1, y1)", :green, :left, :vcenter)
       point(x2, y2, "　(x2, y2)", :red, :left, :vcenter)
   end
end;

算額（その597）

算額（その597）

七六 北埼玉郡騎西町中種足 雷神社 明治5年(1872)
埼玉県立図書館：埼玉県史料集 第二集『埼玉の算額』，昭和44年，誠美堂印刷所，埼玉県与野市.

東京都中央区 福徳神社 令和2年(2020)
http://www.wasan.jp/tokyo/hukutoku1.html

キーワード：正九角形2個，外円，三角形9個

第4問. 大小の正9角形の頂点を線分で結び，三角形と小9角形の面積を等しくなるようにする。大きい9角形の一辺が 1 のとき，小さい9角形の一辺はいかほどか。

これは，術にもあるように簡単で，暗算でもできる。
9 個の三角形は相互に相似で，小9角形の面積は三角形の面積に等しいならば，小9角形は大9角形の 1/10 の面積である。相似比は 1:(1/√10) である。
つまり，大9角形の一辺の長さが 1 のとき，小9角形の一辺の長さは 0.31622776601683794 である。

1/√10

   0.31622776601683794

連立方程式を立てて解くほうが面倒だ。

三角形 BAR において，∠BAR = 40° で，第二余弦定理を使う。
BR^2 = AB^2 + AR^2 - 2AB*AR*cos(2pi/9)
大きい正9角形が内接する円の半径を R とする。
小さい正9角形の一辺の長さを L とする。
小さい正9角形が内接する円の半径 r は R の 1/√10 倍である。
AR = AB + L

include("julia-source.txt");

using SymPy

@syms R::positive, a::positive, c::positive, L::positive,
     x::negative, y::positive  # x < 0

x0 = R*cosd(Sym(40))
y0 = R*sind(Sym(40))
c = 2R*sind(Sym(20))
L = 2R*sind(Sym(20))/sqrt(Sym(10))  # c/sqrt(Sym(10))
eq1 = (x0 - x)^2 + (y0 - y)^2 - a^2
eq2 = (R - x)^2 + y^2 - (a + L)^2
eq3 = a^2 + (a + L)^2 -2a*(a + L)*cosd(Sym(40)) - c^2;

ans_a = solve(eq3, a)[1] |> simplify
ans_a |> println

   sqrt(10)*R*(-sin(pi/9) + sqrt(sin(pi/9)^2 + 9))/10

eq1 = eq1(a => ans_a) |> expand |> simplify
eq2 = eq2(a => ans_a) |> expand |> simplify
res = solve([eq1, eq2], (x, y))[1]

   (R*(-10*sqrt(sin(pi/9)^2 + 9)*sin(pi/9)^2 - (36*cos(2*pi/9) + 56)*sin(pi/9)^3 + (2 - cos(pi/9))*sqrt(sin(pi/9)^2 + 9) + 10*(2 - cos(pi/9))*sin(pi/9))/(80*sin(pi/9)^3), -R*(-18*sqrt(3)*cos(pi/9) - 4*sqrt(19/2 - cos(2*pi/9)/2)*cos(pi/9) + 2*sqrt(19/2 - cos(2*pi/9)/2) + 20*sin(pi/9) + 34*sin(2*pi/9))/(160*sin(pi/9)^2))

@syms t, u
res[1](sin(PI/9) => t, cos(PI/9) => u) |> expand |> simplify |> println

   R*(t^3*(-92 + 72*sin(pi/9)^2) - 10*t^2*sqrt(t^2 + 9) + 10*t*(2 - u) + (2 - u)*sqrt(t^2 + 9))/(80*t^3)

res[2](sin(PI/9) => t, cos(PI/9) => u) |> expand |> simplify |> println

   R*(-20*t + 4*u*sqrt(19/2 - cos(2*pi/9)/2) + 18*sqrt(3)*u - 34*sin(2*pi/9) - 2*sqrt(19/2 - cos(2*pi/9)/2))/(160*t^2)

内側の正9角形の一辺の長さ L = 0.316228

その他のパラメータは以下の通り。

   外側の正9角形の外接円の半径 R = 1.4619;  外側の正9角形の一辺の長さ c = 1
   内側の正9角形の外接円の半径 r = 0.462294;  内側の正9角形の一辺の長さ L = 0.316228
   a = 1.23775;  x = -0.0218825;  y = 0.461776;  x0 = 1.11988;  y0 = 0.939693

function draw(c, more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   t = sind(20)
   t2 = sind(40)
   u = cosd(20)
   u2 = cosd(40)
   R = c/(2t)
   r = R/√10
   L = 2R*t/√10
   @printf("外側の正9角形の外接円の半径 R = %g;  外側の正9角形の一辺の長さ c = %g\n", R, c)
   @printf("内側の正9角形の外接円の半径 r = %g;  内側の正9角形の一辺の長さ L = %g\n", r, L)
   a = √10R*(sqrt(t^2 + 9) - t)/10
   x = R*(t^3*(72t^2 - 92) - 10t^2*sqrt(t^2 + 9) + 10t*(2 - u) + (2 - u)*sqrt(t^2 + 9))/(80t^3)
   y = R*(4u*sqrt(19/2 - u2/2) - 20t+ 18√3u - 34t2 - 2sqrt(19/2 - u2/2))/(160t^2)
   θ = atand(y, x)
   n = 9
   outerθ = 0:40:360
   outerx = @. R*cosd(outerθ)
   outery = @. R*sind(outerθ)
   innerθ = outerθ .+ θ
   innerx = @. r*cosd(innerθ)
   innery = @. r*sind(innerθ)
   @printf("a = %g;  x = %g;  y = %g;  x0 = %g;  y0 = %g\n", a, x, y, outerx[2], outery[2])
   plot()
   circle(0, 0, R)
   circle(0, 0, r, :gray90)
   plot!(outerx, outery, color=:blue, lw=0.5)
   for i in 1:n + 1
       segment(outerx[i], outery[i], innerx[i], innery[i], :green)
   end
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
       point(innerx[1], innery[1], "   A:(x,y)", :green, :left, :vcenter)
       point(outerx[2], outery[2], " B:(x0,y0)", :blue, :left, :vcenter)
       point(R, 0, " R:(R,0)", :blue, :left, :bottom, delta=delta/2)
   end
end;

算額（その596）

算額（その596）

Tony さんの問題
http://takasakiwasan.web.fc2.com/gunnsann/pdf/2019_04_02_1.pdf

外円の中に甲円 5 個，乙円 5 個が入っている。甲円は互いに外接し，外円に内接している。乙円は互いに外接し，甲円とも外接している。
甲円の直径が 74 寸のとき，乙円の直径は以下ほどか。

外円の半径と中心座標を R, (0, 0)
甲円の半径と中心座標を r1, (x1, y1); x1 = r1, y1 = (R - r1)*cosd(36)
乙円の半径と中心座標を r2, (0, y2)
とおき，以下の連立方程式を解く。

include("julia-source.txt");

using SymPy

@syms R::positive, r1::positive, r2::positive, y2::positive;
eq1 = (R - r1)*sind(Sym(36)) - r1
eq2 = r1^2 + ((R - r1)*cosd(Sym(36))- y2)^2 - (r1 + r2)^2
eq3 = y2*sind(Sym(36)) - r2
res = solve([eq1, eq2, eq3], (R, r2, y2))

   2-element Vector{Tuple{Sym, Sym, Sym}}:
    (sqrt(5)*r1*sqrt(10 - 2*sqrt(5))/10 + r1 + r1*sqrt(10 - 2*sqrt(5))/2, r1*(-36*sqrt(10) - 80*sqrt(2) + 37*sqrt(25 - 5*sqrt(5)) + 83*sqrt(5 - sqrt(5)))/(sqrt(5 - sqrt(5))*(21*sqrt(5) + 47)), -8*sqrt(5)*r1/(sqrt(5) + 5) + 2*r1*(3*sqrt(10) + 10*sqrt(2))/(sqrt(5 - sqrt(5))*(2*sqrt(5) + 5)))
    (sqrt(5)*r1*sqrt(10 - 2*sqrt(5))/10 + r1 + r1*sqrt(10 - 2*sqrt(5))/2, r1*(80*sqrt(2) + 36*sqrt(10) + 37*sqrt(25 - 5*sqrt(5)) + 83*sqrt(5 - sqrt(5)))/(sqrt(5 - sqrt(5))*(21*sqrt(5) + 47)), 8*sqrt(5)*r1/(sqrt(5) + 5) + 2*r1*(3*sqrt(10) + 10*sqrt(2))/(sqrt(5 - sqrt(5))*(2*sqrt(5) + 5)))

2 組の解が得られるが，最初のものが適解である。

乙円の直径は 23.0026755202222 である。

2res[1][2](r1 => 74/2).evalf() |> println

   23.0026755202222

その他のパラメータは以下の通り。

   乙円の直径 = 23.0027;  R = 99.9482;  r2 = 11.5013;  y2 = 19.5672;  x1 = 37;  y1 = 50.9261

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   plot()
   r1 = 74/2
   (R, r2, y2) = (
       (sqrt(5)*r1*sqrt(10 - 2*sqrt(5))/10 + r1 + r1*sqrt(10 - 2*sqrt(5))/2,
       r1*(-36*sqrt(10) - 80*sqrt(2) + 37*sqrt(25 - 5*sqrt(5)) + 83*sqrt(5 - sqrt(5)))/(sqrt(5 - sqrt(5))*(21*sqrt(5) + 47)),
       -8*sqrt(5)*r1/(sqrt(5) + 5) + 2*r1*(3*sqrt(10) + 10*sqrt(2))/(sqrt(5 - sqrt(5))*(2*sqrt(5) + 5)))
   )
   x1 = r1
   y1 = (R - r1)*cosd(Sym(36))
   @printf("乙円の直径 = %g;  R = %g;  r2 = %g;  y2 = %g;  x1 = %g;  y1 = %g\n", 2r2, R, r2, y2, x1, y1)
   circle(0, 0, R, :red)
   for i in 1:5
       x = cosd((i - 1)*72 + 54)*(R - r1)
       y = sind((i - 1)*72 + 54)*(R - r1)
       circle(x, y, r1, :blue)
       x = cosd((i - 1)*72 + 18)*y2
       y = sind((i - 1)*72 + 18)*y2
       circle(x, y, r2, :green)
   end
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
       point(0, y2, " r2,(0,y2)", :black, :left, :bottom, delta=delta/3)
       point(x1, y1, "r1,(x1,y1)", :blue, :center, delta=-delta/2)
   end
end;

算額（その595）

算額（その595）

長崎市 鎮西大社諏訪神社 明治20年(1887)
米光丁: 長崎県の和算の概説
http://hyonemitsu.web.fc2.com/Nagasakiwasan.pdf

問題 20. 外円の中に正六角形を入れる。正六角形の矢の長さが 24 寸，内側の正六角形の一辺の長さが 15 寸のとき，外円の直径はいかほどか。

内側の正六角形の一辺の長さを r とする。
点A(x,y) は内側の正六角形が内接する半径 R 円周上にある。図の AB は正六角形の矢，AR は矢の長さから内側の正六角形の一辺の長さを差し引いたものになっている。三角形 ABR において第二余弦定理を適用する。

include("julia-source.txt");

using SymPy

@syms R::positive, 矢::positive, r::positive, a::positive, b::positive,
     x::positive, y::negative

r = 15
矢 = 24
a = 矢
b = sqrt((R - x)^2 + y^2);

eq1 = a^2 + b^2 - a*b - R^2
eq2 = b + r - 矢
eq3 = x^2 + y^2 - r^2

res = solve([eq1, eq2, eq3], (x, y, R))

   1-element Vector{Tuple{Sym, Sym, Sym}}:
    (195/14, -45*sqrt(3)/14, 21)

外円の半径は 21 である。

上の連立方程式において，「r」, 「矢」 を変数のままで，[eq1, eq2] から (x, R) で解くと以下のようになる。

@syms R::positive, 矢::positive, r::positive, a::positive, b::positive,
     x::positive, y::negative

a = 矢
b = sqrt((R - x)^2 + y^2);

eq1 = a^2 + b^2 - a*b - R^2
eq2 = b + r - 矢

res = solve([eq1, eq2], (x, R))

   2-element Vector{Tuple{Sym, Sym}}:
    (-sqrt(-(-r + y + 矢)*(r + y - 矢)) + sqrt(r^2 - 2*r*矢 + 2*矢^2 - 矢*sqrt(r^2 - 2*r*矢 + 矢^2)), sqrt(r^2 - 2*r*矢 + 2*矢^2 - 矢*sqrt(r^2 - 2*r*矢 + 矢^2)))
    (sqrt(-(-r + y + 矢)*(r + y - 矢)) + sqrt(r^2 - 2*r*矢 + 2*矢^2 - 矢*sqrt(r^2 - 2*r*矢 + 矢^2)), sqrt(r^2 - 2*r*矢 + 2*矢^2 - 矢*sqrt(r^2 - 2*r*矢 + 矢^2)))

2組の解が得られる。x の式は y も未知数として含むが，R の式はどちらも同じ式になり，「r」 と 「矢」のみからなる。
SymPy では簡約化できないが手動で以下のように簡約化できる。

外円の半径は得られた式を簡約化して，sqrt(r^2 - r*矢 + 矢^2) である。

R = sqrt(r^2 - r*矢 + 矢^2)
R(r => 15, 矢 => 24).evalf() |> println

   21.0000000000000

正六角形の矢の長さが 24 寸，内側の正六角形の一辺の長さが 15 寸のとき，外円の直径は 42 寸である。

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r = 15
   矢 = 24
   (x, y, R) =  (195/14, -45*sqrt(3)/14, 21)
   θ = atand(y, x)
   n = 7
   outerx = Vector{Float64}(undef, n)
   outery = Vector{Float64}(undef, n)
   innerx = Vector{Float64}(undef, n)
   innery = Vector{Float64}(undef, n)
   plot()
   for i in 1:n
       outerx[i] = cosd((i - 1)*60)*R
       outery[i] = sind((i - 1)*60)*R
       innerx[i] = cosd((i - 1)*60 + θ)*r
       innery[i] = sind((i - 1)*60 + θ)*r
   end
   circle(0, 0, R)
   circle(0, 0, r, :gray90)
   plot!(outerx, outery, color=:blue, lw=0.5)
   for i in 2:7
       segment(outerx[i], outery[i], innerx[i-1], innery[i-1], :green)
   end
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
       point(R, 0, " R(R,0)", :blue, :left, :bottom, delta=delta/2)
       point(r, 0, " r", :magenta, :left, :bottom, delta=delta/2)
       point(x, y, "A(x,y)  ", :green, :right, :vcenter)
       point(innerx[1], innery[1], "A(x,y)  ", :green, :right, :vcenter)
       point(outerx[2], outery[2], "B(R*cos(π/3),R*sin(π/3)", :blue, :center, :bottom, delta=delta)
   end
end;

算額（その594）

算額（その594）

長崎市 鎮西大社諏訪神社 明治20年(1887)
米光丁: 長崎県の和算の概説
http://hyonemitsu.web.fc2.com/Nagasakiwasan.pdf

問題 19. 大円の中に中円を 2 個入れる。大円の直径が 40 寸，矢の長さが 10 寸のとき，中円の直径はいかほどか。

大円の半径と中心座標を R, (0, 0)
中円の半径と中心座標を r, (r, R - 矢 - r)
とおき，以下の方程式を解く。

include("julia-source.txt");

using SymPy

@syms R::positive, 矢::positive, r::positive
eq1 = r^2 + (R - 矢 -r)^2 - (R -r)^2
res = solve(eq1, r)[1] |> println

   sqrt(2)*sqrt(R)*sqrt(矢) - 矢

中円の直径は「大円の直径と矢の積の平方根から矢を引いて 2 倍する」

大円の直径が 40 寸，矢の長さが 10 寸のとき，中円の直径は 20 寸である。

(sqrt(40*10) - 10)*2 |> println

   20.0

function draw(R, 矢, more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   # (R, 矢) = (40//2, 10)
   r = sqrt(2R*矢) - 矢
   @printf("大円の直径 = %g;  矢 = %g;  中円の直径 = %g\n",  2R, 矢, 2r)
   plot()
   segment(0, R, 0, R - 矢, lw=2)
   x1 = sqrt(R^2 - (R - 矢)^2)
   segment(-x1, R - 矢, x1, R - 矢, :red)
   x2 = sqrt(R^2 - (R - 矢 - 2r)^2)
   segment(-x2, R - 矢 - 2r, x2, R - 矢 - 2r, :red)
   circle(0, 0, R, :blue)
   circle(r, R - 矢 - r, r, :orange)
   circle(-r, R - 矢 - r, r, :orange)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
       point(r, R - 矢 - r, "中円:r,(r,R-矢-r)", :orange, :center, delta=-delta)
       point(0, R - 矢/2, " 矢", :black, :left, :vcenter, mark=false)
       point(0, R, " R", :blue, :left, :bottom, delta=delta/2)
   end
end;

 

算額（その593）

算額（その593）

長崎市 鎮西大社諏訪神社 明治20年(1887)
米光丁: 長崎県の和算の概説
http://hyonemitsu.web.fc2.com/Nagasakiwasan.pdf

問題 12. 外円の中に正三角形と大円，小円を入れる。外円の直径が 50 寸のとき小円の直径はいかほどか。

外円の半径と中心座標を R, (0, 0)
小円の半径と中心座標を r, (0, R - R/2 - r)
必要はないが，大円の半径と中心座標は R/2, (0, 0)
とおき，以下の方程式を解く。

include("julia-source.txt");

using SymPy

@syms R, r
eq1 = r/(R - R/2 - r) - 1//2
res = solve(eq1, r)[1]
res |> println

   R/6

小円の半径は外円の半径の 1/6 である。
外円の直径が 50 寸のとき，小円の直径は 50/6 ≒ 8.33333 である。

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   R = 50/2
   r = R/6
   @printf("小円の直径 = %g;  R = %g;  r = %g\n", 2r, R, r)
   plot([R*cosd(30), 0, -R*cosd(30), R*cosd(30)], [-R*sind(30), R, -R*sind(30), -R*sind(30)], color=:gray, lw=0.5)
   circle(0, 0, R, :blue)
   circle(0, 0, R/2, :orange)
   circle(0, R/2 + r, r)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
       point(0, R/2 + r, " 小円:r,(0,R/2+r)", :black, :left, :vcenter)
       point(0, R/2, " R/2+r", :black, :left, delta=-delta)
       point(0, R, " R", :blue, :left, :bottom, delta=delta/2)
   end
end;

算額（その592）

算額（その592）

長崎市 鎮西大社諏訪神社 明治20年(1887)
米光丁: 長崎県の和算の概説
http://hyonemitsu.web.fc2.com/Nagasakiwasan.pdf

問題 11. 外円の中に甲円，乙円，丙円画は一致得る。甲円の直径が 14 寸のとき，乙円の直径はいかほどか。

下部にある甲円，乙円と丙円を対象にすれば，方程式を立てるまでもなく解を求めることができる。

外円の半径と中心座標を R, (0, 0)
甲円の半径と中心座標を r1, (0, r1 - R)
乙円の半径と中心座標を r2, (0, r2 - R)
丙円の半径と中心座標を r3, (0, 0)
として以下の連立方程式を解く。

include("julia-source.txt");

using SymPy

@syms R, r1, r2, r3
eq1 = r1 - (2R - r1)/2
eq2 = r2 - R/4
eq3 = r3 - (2r1 - R)
res = solve([eq1, eq2, eq3], (R, r2, r3))

   Dict{Any, Any} with 3 entries:
     r3 => r1/2
     R  => 3*r1/2
     r2 => 3*r1/8

乙円の半径は，甲円の半径の 3/8 倍である。
甲円の直径が 14 寸のとき，乙円の直径は 14*(3/8) = 5.25 寸である。
算額の答えでは 10.01 寸になっているが，間違いであろう。

r1 = 14/2
(3*r1/8, 3*r1/2, r1/2)

   (2.625, 10.5, 3.5)

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r1 = 14/2
   (r2, R, r3) = (3*r1/8, 3*r1/2, r1/2)
   @printf("乙円の直径 = %g;  R = %g;  r1 = %g;  r2 = %g;  r3 = %g\n", 2r2, R, r1, r2, r3)
   plot([R*cosd(30), 0, -R*cosd(30), R*cosd(30)], [-R*sind(30), R, -R*sind(30), -R*sind(30)], color=:gray, lw=0.5)
   circle(0, 0, R, :blue)
   circle(0, 0, r3, :orange)
   rotate((R - r1)*cosd(30), (R - r1)*sind(30), r1, :green)
   rotate((R - r2)*cosd(30), (R - r2)*sind(30), r2)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
       point(0, r1 - R, " r1-R", :green, :left, :bottom, delta=1.5delta)
       point(0, r2 - R, " r2-R", :red)
       point(0, r3, " r3", :orange, :left, :bottom, delta=delta)
       point(0, 2r1-R, "2r1-R ", :green, :right, :bottom, delta=delta)
   end
end;

 

算額（その591）

算額（その591）

長崎市 鎮西大社諏訪神社 明治20年(1887)
米光丁: 長崎県の和算の概説
http://hyonemitsu.web.fc2.com/Nagasakiwasan.pdf

問題 9. 外円の中に正三角形と菱形を入れる。外円の直径が 60 寸のとき，菱形の一辺の長さはいかほどか。

左右にあるのは大きな正三角形と相似比が 2:1 の正三角形であるから，その一辺の長さが菱形の一辺の長さである。
外円の半径を R とすると，菱形の一辺の長さは √3R/2 である。
外円の直径が 60 寸のとき，菱形の一辺の長さは 25.980762113533157 寸である。

R = 60//2
√3R/2

   25.980762113533157

include("julia-source.txt");

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   R = 60//2
   l = √3R/2
   @printf("菱形の一辺の長さ = %g;  R = %g\n", l, R)
   (Rsin, Rcos) = R .* (sind(30), cosd(30))
   plot([0, Rcos/2, 0, -Rcos/2, 0], [-Rsin, Rsin/2, R, Rsin/2, -Rsin], color=:red, lw=1)
   plot!([-Rcos/2, -Rcos, Rcos, Rcos/2], [Rsin/2, -Rsin, -Rsin, Rsin/2], color=:red, lw=0.5)
   circle(0, 0, R, :blue)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
   end
end;

 

算額（その590）

算額（その590）

長崎市 鎮西大社諏訪神社 明治20年(1887)
米光丁: 長崎県の和算の概説
http://hyonemitsu.web.fc2.com/Nagasakiwasan.pdf

問題 7. 外円の中に菱形と正方形を入れる。長矢と短矢の長さが 18 寸，8 寸のとき，外円の直径はいかほどか。

外円の半径と中心座標を R, (0, 0)
正方形の一辺の長さを 2a とする。
菱形の長径と短径を 2x, 2y とする。
長矢，短矢の長さは x - a, y - a である。

以下の連立方程式を解く。

include("julia-source.txt");

using SymPy

@syms R::positive, a::positive, 長矢::positive, 短矢::positive
eq1 = a + 長矢 - R
eq2 = 短矢/a - (a + 短矢)/R
solve([eq1, eq2], (R, a))

   1-element Vector{Tuple{Sym, Sym}}:
    (sqrt(短矢)*sqrt(長矢) + 長矢, sqrt(短矢)*sqrt(長矢))

外円の半径は「短矢と長矢の積の平方根に長矢を加える」ことで得られる。
長矢と短矢の長さが 18 寸，8 寸のとき，外円の半径は 30 寸，直径は 60 寸である。

(長矢, 短矢) = (18, 8)
sqrt(長矢*短矢) + 長矢

   30.0

ちなみに正方形の一辺の長さは「短矢と長矢の積の平方根」= sqrt(長矢*短矢) = sqrt(18*8) = 12 寸である。

using Plots

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (長矢, 短矢) = (18, 8)
   (R, a) = (sqrt(短矢)*sqrt(長矢) + 長矢, sqrt(短矢)*sqrt(長矢))
   @printf("外円の直径 = %g;  R = %g;  a = %g\n", 2R, R, a)
   plot([0, 30, 0, -30, 0], [-20, 0, 20, 0, -20], color=:green, lw=0.5)
   plot!([12, 12, -12, -12, 12], [-12, 12, 12, -12, -12], color=:red, lw=0.5)
   circle(0, 0, R, :blue)
   segment(0, a, 0, a + 短矢, lw=3)
   segment(a, 0, a + 長矢, 0, lw=3)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
       point(R, 0, " R", :blue, :left, delta=-delta/2)
       point(R, 0, " x", :green, :left, :bottom, delta=delta/2)
       point(a, 0, "a ", :red, :right, delta=-delta/2)
       point(0, a, " a", :red, :left, :top, delta=-delta/2)
       point(0, a + 短矢, " y", :green, :left, :bottom, delta=delta/2)
       point(0, a + 短矢/2, " 短矢", :black, :left, :vcenter)
       point(a + 長矢/2, 0, " 長矢", :black, :center, :bottom, delta=delta/2)
   end
end;

算額（その589）

算額（その589）

長崎市 鎮西大社諏訪神社 明治20年(1887)
米光丁: 長崎県の和算の概説
http://hyonemitsu.web.fc2.com/Nagasakiwasan.pdf

問題 3. 外円内に甲円，乙円，丙円を入れる。甲円，乙円の直径が 20 寸，8 寸のとき，丙円の直径はいかほどか。

問では，外円内にある三角形が直角三角形であることは言及されていない。しかし答は直角三角形でなければ導けないので，ここでも直角三角形と仮定して答えを求める。直角三角形であるならば，斜辺は外円の中心を通る。

外円の半径と中心座標を R, (0, 0);  R = 2r1
甲円の半径と中心座標を r1, (x1, y1)
乙円の半径と中心座標を r2, (0, r2 - R)
丙円の半径と中心座標を r3, (r3 - R, 0)
とおき，以下の連立方程式を解く。

include("julia-source.txt");

using SymPy

@syms R::positive, r1::positive, r2::positive, r3::positive, x1::positive, y1::positive

R = 2r1
eq1 = 4*R^2 - ((2R - 4r2)^2 + (2R - 4r3)^2)
eq3 = x1^2 + y1^2 - (R - r1)^2
eq4 = y1/x1 * (2r2 - R)/(R - 2r3) + 1
res = solve([eq1, eq3, eq4], (r3, x1, y1))

   2-element Vector{Tuple{Sym, Sym, Sym}}:
    ((r1^3 + r1^2*sqrt(r2)*sqrt(2*r1 - r2) - 2*r1^2*r2 - 2*r1*r2^(3/2)*sqrt(2*r1 - r2) + r1*r2^2 + r2^(5/2)*sqrt(2*r1 - r2))/(r1 - r2)^2, -r1 + r2, sqrt(r2)*sqrt(2*r1 - r2))
    (r1 - sqrt(r2)*sqrt(2*r1 - r2), r1 - r2, sqrt(r2)*sqrt(2*r1 - r2))

2 組の解が得られるが，2番目のものが適解である。

丙円の半径は r1 - sqrt(r2)*sqrt(2*r1 - r2)

甲円，乙円の直径が 20 寸，8 寸のとき，丙円の直径は 4 寸である。

(r1, r2) = (20, 8) .// 2
2(r1 - sqrt(r2)*sqrt(2*r1 - r2))

   4.0

ちなみに，x1 = 6;  y1 = 8。

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r1, r2) = (20, 8) .// 2
   (r3, x1, y1) = (r1 - sqrt(r2)*sqrt(2*r1 - r2), r1 - r2, sqrt(r2)*sqrt(2*r1 - r2))
   R = 2r1
   @printf("丙円の直径 = %g;  R = %g; r1 = %g;  r2 = %g;  r3 = %g; x1 = %g;  y1 = %g\n", 2r3, R, r1, r2, r3, x1, y1)
   plot([2r3 - R, R - 2r3, 2r3 - R, 2r3 - R], [2r2 - R, 2r2 - R, R - 2r2, 2r2 - R], color=:orange, lw=0.5)
   circle(0, 0, R)
   circle(x1, y1, r1, :magenta)
   circle(0, r2 - R, r2, :blue)
   circle(r3 - R, 0, r3, :green)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
       point(x1, y1, "甲円:r1,(x1,y1)", :magenta, :center, delta=-delta/2)
       point(0, r2 - R, "  乙円:r2,(0,r2-R)", :blue, :left, :vcenter)
       point(r3 - R, 0, "    丙円:r3,(r3-R,0)", :green, :left, :bottom, delta=delta/2)
       point(2r3 - R, R - 2r2, "  (2r3-R,R-2r2)", :black, :left, :vcenter)
       
   end
end;

算額（その588）

算額（その588）

長崎市 鎮西大社諏訪神社 明治20年(1887)
米光丁: 長崎県の和算の概説
http://hyonemitsu.web.fc2.com/Nagasakiwasan.pdf

問題 2. 外円の内部に大円 1 個と，弧に挟まれた小円 6 個を入れる。弧を構成する円の半径は外円の半径と同じである。外円の直径が 40 寸のとき，大円の直径はいかほどか。

外円の半径と中心座標を R, (0, 0)
大円の半径と中心座標を r1, (0, 0)
小円の半径と中心座標を r2, (R - r2, 0)
とおき，以下の連立方程式を解く。

include("julia-source.txt");

using SymPy

@syms R::positive, r1::positive, r2::positive

eq1 = (1 - sqrt(Sym(3))/2)R - r2
eq2 = r1 - (R - 2r2)
res = solve([eq1, eq2], (r1, r2))
res |> println

   Dict{Any, Any}(r2 => -sqrt(3)*R/2 + R, r1 => -R + sqrt(3)*R)

大円の半径は，外円の半径の √3 - 1 倍である。
小円の半径は，外円の半径の 1 -　√3/2 倍である。

外円の直径が 40 寸のとき，大円の直径は 40(√3 - 1) = 29.282032302755088 寸である。

40(√3 - 1)

   29.282032302755088

using Plots

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   R = 40 // 2
   r1 = (√3 - 1)R
   r2 = (1 -　√3/2)R
   @printf("大円の直径 = %g;  R = %g; r1 = %g;  r2 = %g\n", 2r1, R, r1, r2)
   plot()
   circle(0, 0, R)
   circle(0, 0, r1, :magenta)
   rotate(r1 + r2, 0, r2, :green, angle=60)
   for i = 0:5
       circle(2(R - r2)*cosd(60i), 2(R - r2)*sind(60i), R, :blue, beginangle=150 + 60i, endangle=210 + 60i)
   end
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
       point(R, 0, " R", :red, :left, :bottom, delta=delta/2)
       point(r1, 0, "r1 ", :red, :right, :bottom, delta=delta/2)
       point(R - r2, 0, "R-r2", :red, :center, :bottom, delta=delta/2)
   end
end;

 

算額（その587）

算額（その587）

長崎市 鎮西大社諏訪神社 明治20年(1887)
米光丁: 長崎県の和算の概説
http://hyonemitsu.web.fc2.com/Nagasakiwasan.pdf

問題 1. 外円内に正三角形，大円，小円が入っている。大円，小円の直径が 60 寸，48 寸のとき，外円の直径はいかほどか。

外円の半径と中心座標を R, (0, R)
大円の半径と中心座標を r1, (0, r1)
小円の半径と中心座標を r2, (0, r2)
とおき，以下の連立方程式を解く。

include("julia-source.txt");

using SymPy

@syms R::positive, r1::positive, r2::positive, x::positive

x = 2r2 - r1
eq = sqrt(r1^2 - x^2)/(2R - 2r2) - 1/sqrt(Sym(3))
res = solve(eq, R)
res |> println

   Sym[sqrt(3)*sqrt(r2)*sqrt(r1 - r2) + r2]

外円の半径は，sqrt(3)*sqrt(r2)*sqrt(r1 - r2) + r2 で求められる。
大円，中円の直径が 60 寸，48 寸のとき，外円の半径は 44.7846096908265 寸，直径は 89.5692193816530 寸である。

res[1](r1 => 60/2, r2 => 48/2).evalf() |> println
2res[1](r1 => 60/2, r2 => 48/2).evalf() |> println

   44.7846096908265
   89.5692193816530

算額の答えでは 89.568 寸としているが，外円の半径を小数点以下3桁まで求め（切り捨て）44.784 を 2 倍したのかもしれない。

using Plots

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r1, r2) = (60, 48) .// 2
   R = sqrt(3)*sqrt(r2)*sqrt(r1 - r2) + r2
   @printf("外円の直径 = %g;  R = %g; r1 = %g;  r2 = %g\n", 2R, R, r1, r2)
   plot()
   circle(0, R, R)
   circle(0, r1, r1, :blue)
   circle(0, r2, r2, :green)
   x1 = sqrt(r1^2 - (2r2 - r1)^2)
   plot!([-x1, x1, 0, -x1], [2r2, 2r2, 2R, 2r2], color=:black, lw=0.5)
   x2 = (2R - 2r1)/√3
   segment(-x2, 2r1, x2, 2r1, :black)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
       point(0, 2R, " 2R", :red, :left, :bottom, delta=delta/2)
       point(0, 2r1, " 2r1", :blue, :left, :bottom, delta=delta/2)
       point(0, 2r2, " 2r2", :green, :left, :bottom, delta=delta/2)
       point(0, R, " R", :red, :left, :vcenter)
       point(0, r1, " r1", :blue, :left, :vcenter)
       point(0, r2, " r2", :green, :left, :vcenter)
       point(x1, 2r2, "  (x1,2r2)", :black, :left, :vcenter)
       point(x2, 2r1, "  (x2,2r1)", :black, :left, :vcenter)
   end
end;

算額（その586）

算額（その586）

長崎市 鎮西大社諏訪神社 明治20年(1887)
米光丁: 長崎県の和算の概説
http://hyonemitsu.web.fc2.com/Nagasakiwasan.pdf

問題 18. 外円の中に 4 個の円を入れる。外円，中円の直径が 50 寸，30 寸のとき，小円の直径はいかほどか。

外円の半径と中心座標を R, (0, 0)
中円の半径と中心座標を r1, (0, R - r1)
小円の半径と中心座標を r2, (R - r2, 0)
とおき，以下の方程式を解く。

include("julia-source.txt");

using SymPy

@syms R::positive, r1::positive, r2::positive

eq = (R - r2)^2 + (R - r1)^2 - (r1 + r2)^2
res = solve(eq, r2)
res |> println

   Sym[R*(R - r1)/(R + r1)]

小円の半径は，外円の半径と中円の半径の差を外円の半径と中円の半径の和で割り，外円の半径を掛けることで得られる。
外円，中円の直径が 50 寸，30 寸のとき，小円の半径は 6.25 寸，直径は 12.5 寸である。

res[1](R => 50/2, r1 => 30/2) |> println
2res[1](R => 50/2, r1 => 30/2) |> println

   6.25000000000000
   12.5000000000000

算額の答えは「外円の直径は四十三寸五八」となっているが何らかの誤りであろう。

using Plots

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (R, r1) = (50, 30) .// 2
   r2 = R*(R - r1)/(R + r1)
   @printf("小円の直径 = %g;  R = %g; r1 = %g;  r2 = %g\n", 2r2, R, r1, r2)
   plot()
   circle(0, 0, R)
   circle(0, R - r1, r1, :blue)
   circle(0, r1 - R, r1, :blue)
   circle(R - r2, 0, r2, :magenta)
   circle(r2 - R, 0, r2, :magenta)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
       point(R, 0, " R", :red, :left, :bottom, delta=delta/2)
       point(0, R - r1, " 中円:r1,(0,R-r1)", :blue, :left, :vcenter)
       point(R - r2, 0, "小円:r2\n(R-r2, 0) ", :magenta, :center, :top, delta=-delta)
   end
end;