
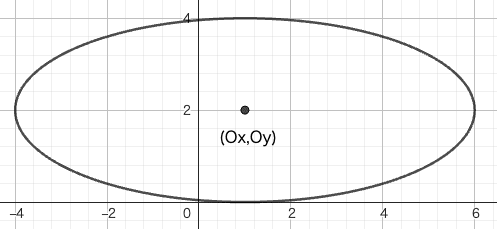
Curve(Ox + a * cos(t), Oy + b * sin(t), t, 0, 2π)
MacOS Sequoia 15.x で,ディレクトリ表示中のファイル・ディレクトリの変更日の時刻表示が12時制になているのを24時制にする方法
ターミナルで 24時間制を強制する方法
1.ターミナルを開く(「アプリケーション」→「ユーティリティ」→「ターミナル」)
2.以下のコマンドを入力し、Enter を押す
defaults write NSGlobalDomain AppleICUForce24HourTime -bool true3.Finder を再起動
killall Finderまたは、ログアウト&ログインすることで設定を適用できます。
現在の設定を確認する
設定が適用されているか確認するには、以下のコマンドを実行してください。
defaults read NSGlobalDomain AppleICUForce24HourTimeこれが 1 になっていれば 24時間制が有効になっています。
元に戻したい場合
12時間制に戻したい場合は、以下のコマンドを実行してください。
defaults write NSGlobalDomain AppleICUForce24HourTime -bool false
killall FinderJulia で RGB による色指定を行うには、主に Colors.jl パッケージを使用します。このパッケージでは、RGB(r, g, b) 形式で色を指定できます。r, g, b は 0.0 から 1.0 の範囲の Float64 値です。
1. Colors.jl のインストール
まず Colors.jl をインストールします。
using Pkg
Pkg.add("Colors")2. RGB 色の指定
using Colors
color1 = RGB(1.0, 0.0, 0.0) # 赤
color2 = RGB(0.0, 1.0, 0.0) # 緑
color3 = RGB(0.0, 0.0, 1.0) # 青
color4 = RGB(0.5, 0.5, 0.5) # グレー3. 255スケールのRGB値を使う場合
通常の 0-255 スケールの RGB 値を使いたい場合は、RGB24 を使うか、255 で割ることで対応できます。
color5 = RGB(255/255, 128/255, 64/255) # RGB(1.0, 0.5, 0.25)
color6 = RGB24(255, 128, 64) # `RGB24` は 8ビット整数表現RGB24 は 8 ビット整数 (0-255) での指定が可能ですが、内部的には RGB に変換されます。
4. HTML カラーコード (16進数) の使用
16進数のカラーコードから RGB に変換するには parse を使います。
color7 = parse(Colorant, "#FF8040") # オレンジ系5. 色の成分取得
定義した色から R, G, B の成分を取得するには以下のようにします。
r = red(color5) # 1.0
g = green(color5) # 0.5
b = blue(color5) # 0.256. 可視化例 (Plots.jl を使用)
例えば、Plots.jl を使って作成したプロットに色を適用することも可能です。
using Plots
plot(1:10, rand(10), color=color5, lw=3)このように Colors.jl を使うと、RGB 形式で柔軟に色を指定できます。
Julia で統計解析
2024/7/18 にバージョンアップ
https://r-de-r.github.io/stats/Julia-stats1.html
https://r-de-r.github.io/stats/Julia-stats2.html
https://r-de-r.github.io/stats/Julia-stats3.html
https://r-de-r.github.io/stats/Julia-stats4.html
https://r-de-r.github.io/stats/Julia-stats5.html
https://r-de-r.github.io/stats/Julia-stats6.html
https://r-de-r.github.io/stats/Julia-stats7.html
https://r-de-r.github.io/stats/Julia-stats8.html
https://r-de-r.github.io/stats/Julia-stats9.html
第 1 章 Julia の実行環境
1. 必要なファイルをダウンロードする
2. Julia のインストール
3. Julia を起動し終了する
4. 作業ディレクトリを変える
5. Julia の環境設定をする
5.1. startup.jl ファイルがあるかを確認
5.2. config がなかった場合
5.3. startup.jl がある場合
5.4. 変更内容の確認
6. オンラインヘルプを使う
7. パッケージを利用する
8. エディタを使う
8.1. Atom
8.2. Jupyter lab
9. 結果を保存する
第 2 章 データの入出力
1. データをデータフレームへ読み込む
1.1. Excel のワークシートファイル
1.2. CSV ファイル
1.2.1. 典型的な CSV ファイル
1.2.2. 一般の CSV ファイル
1.2.3. CSV.read の引数
1.3. インターネット上の CSV ファイル
1.4. モニター上に表示された表をデータフレームに読み込む
1.5. クリップボードにコピーした内容をデータフレームにする
1.6. 文字列行から入力する
1.7. エンコーディングの違うファイルを読む
1.8. デリミタで区切られていない固定書式ファイルを読む
2. データフレームを CSV ファイルに書き出す
2.1. CSV.write の引数
第 3 章 データフレームの取り扱い
1. データを使用するための準備
1.1. 既存のデータを使用する
1.2. 自前のデータ
2. データフレームの概要
2.1. データフレームの大きさ
2.2. データフレームの変数名
2.3. データフレームの表示
3. データフレームのコピーは copy() で
4. 空データフレーム
5. データフレームの列の参照
6. データフレームの行の参照
7. データフレームの列名の変更
8. 列の抽出
9. 指定された列を削除する
10. 行の抽出
11. 行の削除
12. 重複を除き,ユニークな行のみを含むデータフレームを作る
13. 欠損値を含む行か含まない行か
14. 欠損値を含まない行を抽出する
15. データフレームの列方向連結
16. データフレームの行方向連結
16.1. cols = :setequal, cols=:orderequal
16.2. cols = :intersect
16.3. cols = :subset
16.4. cols = :union
17. データフレームの最終行の次に 1 行追加する
18. 行を繰り返してデータフレームを作る
19. データフレームに列を挿入する
20. データフレームの要素から新しいデータフレームを作る
21. データフレームの各列に関数を施す
22. ソート(並べ替え)
22.1. ソートされているかをチェックする
22.2. ソートの順番を決める
22.3. 並べ替えベクトルを返す
23. 行の包含
23.1. df1 と df2 のすべての組み合わせを作る crossjoin
23.2. df1 の行のうち,df2 に含まれない行を抽出する antijoin
23.3. df1 に,df2 をマージする innerjoin
23.4. df1 に,df2 をマージする leftjoin
23.5. df1 に,df2 をマージする outerjoin
23.6. df2 に,df1 をマージする rightjoin
23.7. 両方に存在する項目のみでマージする semijoin
24. 欠損値のリストワイズ除去
25. ロングフォーマット(縦長データフレーム)に変換する
26. ワイドフォーマット(横長データフレーム)に変換する
27. データフレームをグループ変数に基づいて分割する
27.1. グループ分けされたデータフレームを抽出する
27.2. グループ化されたデータフレームに関する情報
27.3. 親データフレームを返す
28. 列ごとに関数を適用する
29. 行ごとに関数を適用する
30. クエリーによる操作例
30.1. 要素に関数を適用する @map コマンド
30.2. 条件を満たす行を抽出 @filter コマンド
30.3. データフレームのグループ化 @groupby コマンド
30.4. データのソート @orderby,@orderby_descenidng,@thenby,@thenby_descending コマンド
30.5. データフレームのマージ @groupjoin コマンド
30.6. データフレームの連結 @join コマンド
30.7. キーと値のペアを展開 @mapmany コマンド
30.8. 要素を取り出す @take コマンド
30.9. 要素を捨てる @drop コマンド
30.10. 重複データを除く @unique コマンド
30.11. 列の選択 @select コマンド
30.12. 列名の変更 @rename コマンド
30.13. 変数変換 @mutate コマンド
30.14. 欠損値行を除く @dropna コマンド
30.15. 欠損値を含まないデータフレーム @dissallowna コマンド
30.16. 欠損値の置き換え @replacena コマンド
31. データフレームを二次元配列に変換する
第 4 章 一変量統計
1. 一変量統計
1.1. 一変数の場合
1.1.1. 基礎統計量
1.1.2. パーセンタイル値
1.1.3. 度数分布
1.2. 複数の変数の場合
1.2.1. eachcol() を使う
1.2.2. describe() を使う
1.2.3. combine(), select()/select!(), transform()/transform!() を使う
1.3. グループごとの記述統計量
1.3.1. describe() を使う
1.3.2. 変数ごとに統計量を一覧表示
2. 二変量統計
2.1. 二重クロス集計表
2.2. 相関係数,共分散
2.2.1. 欠損値を含まない場合
2.2.1.1. それぞれの関数を使う
2.2.1.2. combine() を使う
2.2.2. 欠損値を含む場合
2.2.2.1. それぞれの関数を使う
2.2.2.2. combine() を使う
2.3. 相関係数行列,分散・共分散行列
2.3.1. 欠損値を含まない場合
2.3.2. 欠損値を含む場合
3. 多変量統計
3.1. 多重クロス集計表
第 5 章 離散データの可視化
1. 例示に使用するデータセット
1.1. カテゴリーデータ
2. 棒グラフ
2.1. 一標本の場合
2.2. 二標本以上の場合
2.2.1. 横に並べる棒グラフ
2.2.2. 積み上げ棒グラフ
2.3. 複数のグラフを行列状にまとめて表示する方法
3. 帯グラフ
4. モザイクプロット
5. バルーンプロット
第 6 章 数値データの可視化
1. ヒストグラム
1.1. 一標本の場合
1.2. 複数標本の場合
2. ボックスプロット(箱ひげ図)
3. バイオリンプロット
4. ドットプロット
5. カーネル密度推定の描画
6. Q-Q プロット
7. 散布図
8. カーネル密度推定
9. 散布図行列
10. 作図レシピ
10.1. 二軸グラフ
10.2. Andrews plot
10.3. 星座グラフ
10.4. サンフラワープロット
10.5. レーダーチャート
第 7 章 検定と推定
1. 検定関数関数の呼び出し方
2. 検定関数関数により得られる結果の利用法
3. 分布の検定
3.1. 観察度数が一様かどうかの検定
3.1.1. ピアソンの \\chi^2 検定
3.1.2. 対数尤度比検定(G^2 検定)
3.2. 観察度数が理論比に從うかどうかの検定
3.2.1. ピアソンの \\chi^2 検定
3.2.2. 対数尤度比検定(G^2 検定)
4. 独立性の検定
4.1. ピアソンの \\chi^2 検定
4.2. 対数尤度比検定(G^2 検定)
5. パワーダイバージェンス検定
6. フィッシャーの正確検定
7. 二項検定
8. t 検定
8.1. 一標本の検定(母平均の検定)
8.2. 等分散の場合の t 検定
8.3. 等分散でない場合 Welch の方法
9. マン・ホイットニーの U 検定
10. 符号検定
11. ウィルコクソンの符号付き順位和検定
12. 相関係数の検定
13. 対応のない k 標本(独立 k 標本)
13.1. 一元元配置分散分析
13.2. 一元元配置分散分析(ウェルチの方法)
13.3. クラスカル・ウォリス検定
14. コルモゴロフ・スミルノフ検定
14.1. 1 標本の分布の検定
14.2. 2 標本の分布の差の検定
15. アンダーソン・ダーリング検定
15.1. 1 標本の場合
15.2. k 標本の場合
16. ワルド・ウォルフォビッツ連検定
17. 並べ替え検定(無作為検定)
第 8 章 多変量解析
1. 回帰分析
1.1. 線形最小二乗回帰 Linear Least Square
1.1.1. 単回帰分析
1.1.2. 重回帰分析
1.2. リッジ回帰 Ridge Regression
1.2.1. 説明変数が 1 個の場合
1.2.2. 説明変数が 2 個以上の場合
1.3. GLM パッケージによる回帰分析
1.3.1. 重回帰分析 Ordinary Least Squares Regression
1.3.2. プロビット回帰 Probit Regression
1.3.3. ロジット回帰 Logit Regression
1.4. 多項式回帰
1.4.1. 重回帰プログラムを用いる
1.4.2. 多項式回帰 Polynomials パッケージ
1.5. 指数回帰
1.5.1. 説明変数が 1 個の場合
1.5.2. 説明変数が 2 個以上の場合
1.6. 累乗回帰
1.6.1. 説明変数が 1 個の場合
1.6.2. 説明変数が 2 個以上の場合
1.7. 非線形回帰
2. 判別分析
2.1. 二群判別分析
2.2. 多重判別分析
3. 主成分分析
4. 因子分析
5. 古典的多次元尺度解析
6. クラスター分析
6.1. K-means 法による非階層的クラスター分析
6.2. 階層的クラスター分析
7. カテゴリー変数の取り扱い方
7.1. 重回帰分析の場合
7.2. 判別分析の場合
第 9 章 関数
一辺の長さが R の正方形の中に,半径 R の四分円 2 個と,半径 r の円を描く。
四分円と円の隙間(緑の点が散らばっている領域)の面積をモンテカルロ法により求める。

1000000 個の点を打って,領域内に入った点の割合から面積を推定すると,0.172231*R^2 となった。解析解は 0.17239838239331384*R^2 だったので,解析解を導いた式は間違っていなさそうだ。
using Random, Distributions, StatsBase
R = 1
r = 3R/8
n = 1000000
x = rand(Uniform(0.5, 1.0), n)
y = rand(Uniform(0, 1.0), n)
z = @. (x^2 + y^2 < R^2) && ((x - R/2)^2 + (y - r)^2 > r^2)
2*(R^2/2 * mean(z))
0.172231
こちらにも投稿しておこう。
受験生は log10(2), log10(3) は知っているとの前提で
import math
もともとの数値
(2 * 3 * 5 * 7 * 11 * 13)**10
596421543032951827553785377955490490000000000
それは知らない(わからない)ことにしておいて,
10 乗する数は
2 * 3 * 5 * 7 * 11 * 13
30030
まず,30030 よりほんの少し小さい数を 2, 3, 5 のべき乗の積で作る
2 * 4 * 4 * 5 * 10 * 16, 2**8 * 100
(25600, 25600)
25600**10 の常用対数を取る
10*(8*math.log10(2) + 2)
44.0823996531185
次に,30030 よりほんの少し大きい数を 2, 3, 5 のべき乗の積で作る
2 * 4 * 4 * 6 * 10 * 16, 2**10 * 3 * 10
(30720, 30720)
30720**10 の常用対数を取る
10*(10*math.log10(2) + math.log10(3) + 1)
44.87421211359475
3 つの数値は,同じ桁数になったようだ...
(2 * 3 * 5 * 7 * 11 * 13)**10 の常用対数は 25600 の常用対数より大きく, 30720 の常用対数より小さい
10*(8*math.log10(2) + 2) < math.log10((2 * 3 * 5 * 7 * 11 * 13)**10) < math.log10((2**10 * 3 * 10)**10)
True
さらに,桁数は同じ 45 桁である。
10*(8*math.log10(2) + 2), math.log10((2 * 3 * 5 * 7 * 11 * 13)**10), math.log10((2**10 * 3 * 10)**10)
(44.0823996531185, 44.77555332198981, 44.874212113594744)
某氏のプログラムで(プログラミング言語は何だっていい,言わんとしていることはわかるだろう)
switch mat_ver
case 1
mat_name='R2019a';
case 2
mat_name='R2007b';
case 3
mat_name='ver7.1';
case 4
mat_name='ver5.3';
end
というような類似部分が,何箇所もある。簡明直截ではあるが,ダサい。
name = ['R2019a', 'R2007b', 'ver7.1', 'ver5.3']
mat_name = name[mat_ver]
でいいじゃないか。
更には,中間変数なんぞも不要で,
mat_name = ['R2019a', 'R2007b', 'ver7.1', 'ver5.3'][mat_ver]
のほうが,どれだけわかりやすいか。
こういうプログラムを書く人は信用ならん。
AIの活用には、以下のようなルールが存在します。
-
倫理と法律の尊重: AIの活用は、倫理的な観点や法的な制約を尊重する必要があります。人権やプライバシーの侵害を防ぐために、関連する法律や規制に従うことが重要です。
-
透明性と説明責任: AIシステムが意思決定や推論を行う場合、そのプロセスや基準を透明にする必要があります。ユーザーや関係者に対して説明責任を果たすことで、信頼性と責任を確保します。
-
データの正確性と公平性: AIのトレーニングに使用するデータは、正確性と公平性が確保されている必要があります。バイアスのないデータセットを使用し、アルゴリズムの結果が公正であることを確認するために、定期的な監査や評価を実施することが重要です。
-
プライバシーとセキュリティの保護: AIに関連するデータは、適切なセキュリティ対策を講じて保護されるべきです。個人情報や機密情報の取り扱いには特に注意が必要であり、データの不正利用や漏洩を防ぐための措置を講じることが必要です。
-
人間との協働: AIは人間の補完として活用されるべきです。人間とAIの協力によって相互補完的な強みを引き出し、より効果的な結果を生み出すことが期待されます。AIは人間の意思決定をサポートし、自動化されたプロセスにおける人間の監視や介入が必要な場合もあります。
-
継続的なモニタリングと改善: AIシステムのパフォーマンスや影響を継続的に監視し、必要に応じて改善を行うことが重要です。フィードバックの収集やモデルのアップデートを通じて、AIの正確性や効果性を向上させる取り組みを行います。
これらのルールは、AIの活用において倫理的な枠組みを提供し、AIシステムが社会的な価値を提供するため
るとともに、リスクや潜在的な問題を最小限に抑える役割を果たします。AIの活用には、これらのルールを遵守し、適切なガバナンスと監督を確立することが重要です。
また、AIの活用に関しては、以下のような考慮事項も重要です。
-
ユーザーのインクルージョン: AIシステムは、ユーザーの多様なニーズや能力に対応する必要があります。アクセシビリティやユーザビリティの観点から、利用者がシステムを理解し、利用できるように設計されるべきです。
-
信頼性と責任: AIの活用は、高い信頼性と責任を持つことが求められます。アルゴリズムの誤った判断や結果による悪影響を最小限に抑えるために、信頼性の確保と責任ある運用が必要です。
-
フェアネスと公正性: AIの活用は、公正でバイアスのない結果を提供することが重要です。特定の個人やグループに対する差別や不平等を生じないよう、アルゴリズムの設計やトレーニングデータの選択において公正性を確保する必要があります。
-
透明性と説明可能性: AIの意思決定プロセスが透明で説明可能であることは重要です。ユーザーにとって理解可能であり、必要な場合には説明ができるようなAIシステムの設計と運用が求められます。
-
知識の更新と学習: AIの活用には、最新の知識や技術の継続的な学習が不可欠です。迅速な変化や新たな課題に対応するために、AIシステムの開発者や利用者は常に学習し、技術を進化させる努力を続ける必要があります。
これらのルールと考慮事項に基づいて、AIの活用は社会的な利益を最大化し、持続可能な発展に貢献することが期待されます。
今,テレビでやってた。クロワッサンを作るときに,最適なバターの割合をx%からはじめてx+1%にしてとやって,20年かかってやっと最適な割合を見つけたんですって。
ご苦労様でした。二分法を知っていれば,もっと速く最適な割合が見つかったんでしょうにねえ。
数学は偉大だよ。
-2 の平方根を求めてみる
Python は (-2)**0.5 で求めることができる。しかし,誤差が表示される。虚数単位は j で表される。
>>> (-2)**0.5
(8.659560562354934e-17+1.4142135623730951j)
numpy.sqrt(-2) ではエラーになる。
>>> import numpy as np
>>> np.sqrt(-2)
<stdin>:1: RuntimeWarning: invalid value encountered in sqrt
nan
虚数として与えるとちゃんと計算する。
>>> np.sqrt(-2+0j)
1.4142135623730951j
R ではどうか。
> options(digits=16)
> (-2)^0.5
[1] NaN
> (-2.0+0i)^0.5
[1] 0+1.414213562373095i
Octave はどうか。
>> (-2)^0.5
ans = 8.659560562354932e-17 + 1.414213562373095e+00i
sqrt() は誤差を含まない。
>> sqrt(-2)
ans = 0 + 1.414213562373095i
Julia では?
julia> (-2)^0.5
ERROR: DomainError with -2.0:
Exponentiation yielding a complex result requires a complex argument.
Replace x^y with (x+0im)^y, Complex(x)^y, or similar.
単にエラーを出すだけではなく,解決方法を提案してくれる。
julia> (-2+0im)^0.5
0.0 + 1.4142135623730951im
sqrt() も,解決方法を提案してくれる。
julia> sqrt(-2)
ERROR: DomainError with -2.0:
sqrt will only return a complex result if called with a complex argument. Try sqrt(Complex(x)).
julia> sqrt(Complex(-2))
0.0 + 1.4142135623730951im
以下のプログラムは Julia なのだけど,他の言語でも同じ。
function calc(s1, s2)
# 消費支出 s1 円と飲食費 s2 円からエンゲル係数を計算する。
return s2*100/s1
end
function engel()
s1 = Base.prompt("消費支出? ")
s2 = Base.prompt("飲食費? ")
s1 = parse(Float64, s1)
s2 = parse(Float64, s2)
x1 = calc(s1, s2)
if x1 >= 80
println("エンゲル係数は ", round(Int, x1),
" です。飲食費を使いすぎです。")
else
println("エンゲル係数は ", round(Int, x1), " です。")
end
end
まあそれでもいいのですが,こなれたプログラムならこう書くべき。
つまり,同じプログラム片を何回も(2回でも)書かない。
似たプログラム片,変数名などが出てくると,前に出てきたのと同じなのか,少し違うのかが気にかかる。
同じ部分は繰り返さないようにするし,違うところはそれがはっきりわかるように書く。
ついでに,金額は整数と思うのでそのようにしておく。
function engel()
s1 = Base.prompt("消費支出? ")
s2 = Base.prompt("飲食費? ")
s1 = parse(Int, s1)
s2 = parse(Int, s2)
x1 = calc(s1, s2)
print("エンゲル係数は $(round(Int, x1)) です。")
println(x1 >= 80 ? "飲食費を使いすぎです。" : "")
end
なお,一般的に言えば,オンラインの実行時にコンソールからデータを入力するプログラムは書くべきではない。
更に蛇足
本来のエンゲル係数は,貧困度の測定にある。収入が少ないために,必須である食費支出の割合が多くなることを問題とする。飽食の時代では,有り余る収入に贅沢な食生活の割合を測定するものになっているのかなあ?
そんなこともあるので,ソースは明示しない。



















