「標本分散」ってなんだ?

「不偏分散」の話をするときに，それに対応するものを「標本分散」と呼ぶ人がいる。

「標本から計算した『分散』は母分散の推定値」，ならば不偏分散も『分散』も標本分散ですね。そして，『分散』は母分散から偏っているので，それを不偏にするのが不偏分散。

つまりよく使われている「標本分散」というのは何かというと，正確には「標本から計算した不偏ではない分散」でしょう。英語だと不偏分散は unbiased variance，不偏でない分散は単に variance です（sample variance とは言いません）。

ちなみに，Python では指定しないと不偏ではない分散を計算します（不偏分散は ddof=1 を指定する）が，R や Julia では不偏分散を計算します（R では分散を計算させるオプションがない。Julia では corrected=false を指定する）。

このような曖昧な用語法は，たぶん Excel の和訳が不適切だった名残だと思います。 Excel が日本語されて使えるようになった頃，統計用語の和訳がめちゃくちゃでした。今でも残っている迷訳があります。

Python

>>> import numpy as np
>>> x = np.arange(10) + 1
array([ 1,  2,  3,  4,  5,  6,  7,  8,  9, 10])
>>> np.var(x)
8.25
>>> np.var(x, ddof=1)
9.166666666666666

Julia

julia> using Statistics
julia> x = 1:10
1:10
julia> var(x)
9.166666666666666
julia> var(x, corrected=false)
8.25

R

> x = 1:10
> var(x)
[1] 9.166667
> n = length(x)
> var(x) * (n-1)/n
[1] 8.25

 

 

グラフの作り方って，おもしろいな〜〜。ということ

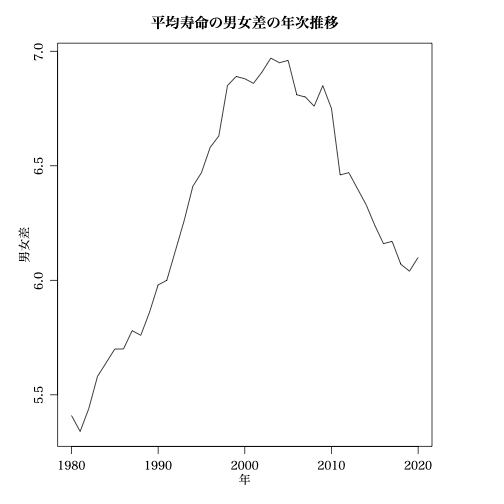
中澤先生が，男女の平均寿命の差について，「格差が拡大してから低下している」とツイートしたそうだ。

https://minato.sip21c.org/im3r/20220129.html

中澤先生の図は（日本語が文字化けしているので，簡略化した）

le0 <- data.frame(
    YEAR = 1980:2020,
    Males = c(73.35, 73.79, 74.22, 74.20, 74.54, 74.78, 75.23, 75.61, 75.54, 75.91,
        75.92, 76.11, 76.09, 76.25, 76.57, 76.38, 77.01, 77.19, 77.16, 77.10,
        77.72, 78.07, 78.32, 78.36, 78.64, 78.56, 79.00, 79.19, 79.29, 79.59,
        79.55, 79.44, 79.94, 80.21, 80.50, 80.75, 80.98, 81.09, 81.25, 81.41, 81.64),
    Females = c(78.76, 79.13, 79.66, 79.78, 80.18, 80.48, 80.93, 81.39, 81.30, 81.77, 
        81.90, 82.11, 82.22, 82.51, 82.98, 82.85, 83.59, 83.82, 84.01, 83.99, 
        84.60, 84.93, 85.23, 85.33, 85.59, 85.52, 85.81, 85.99, 86.05, 86.44, 
        86.30, 85.90, 86.41, 86.61, 86.83, 86.99, 87.14, 87.26, 87.32, 87.45, 87.74))
le0$sexdif <- le0$Females - le0$Males

plot(sexdif ~ YEAR, data=le0, type="l", lty=1, lwd=1, col="black", 
    xlab="年", ylab="男女差",
    main="平均寿命の男女差の年次推移")

により，以下の図を掲示している。

なるほど，「格差が拡大してから低下している」

これを拝見して，なんとなくピンときて私が描いてみた図は

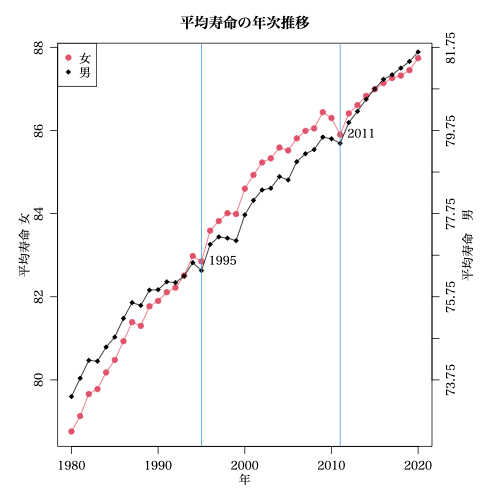
女の平均寿命と，男の平均寿命+6.25 を併記してみた。（6.25 は恣意的に選んだ）

かつて，女の平均寿命は伸び率が大きく，男の平均寿命の伸びを追いかけ，1995年の両者とものカックンをのぞき追いつき追い越した。

そして再びの 2011 年の大ガックンを迎え，女の伸び率は男の伸び率と同じくらいになって，現在に至る。

 

2011年は，　　　東日本大震災のあった年だなあ。それと関係があるのだろうか。人口学にはとんと疎いが，多分関係があるのだろう。

1995年は，　　　何があったっけ。ググッてみた。1位：阪神大震災 ，2位：オウム真理教による地下鉄サリン事件 ， 3位：不良債権で住専やコスモ、木津、兵銀など金融機関の破綻。ガックンの原因はわかったようで，わからない。

 

6.25 は恣意的と書いたが，6.5 だとちょっとイメージが変わる。

2011 年を契機に（?）女の伸び率が低くなっている（?）。

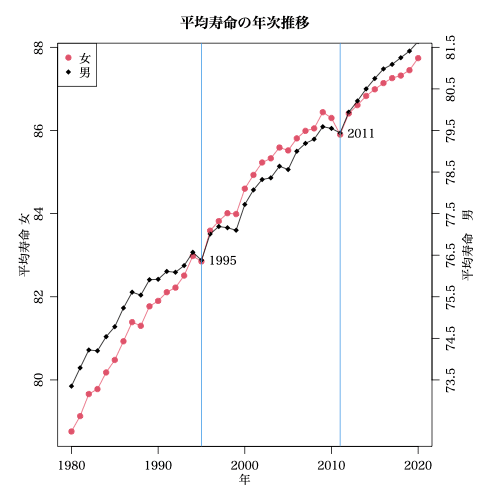
プログラムも載せておくが，最近メッキリ R のプログラミング力が落ちてしまって，恥ずかしい限り。

delta = 6.25
par(mar=c(4, 4, 3, 5), mgp=c(1.8, 0.8, 0))
plot(le0$Females ~ le0$YEAR, col=2, pch=19,
    xlab="年", ylab="平均寿命 女", main="平均寿命の年次推移")
points(le0$Males+ delta ~ le0$YEAR, col=1, pch=18)
lines(le0$Females ~ le0$YEAR, col=2)
lines(le0$Males+ delta ~ le0$YEAR, col=1)
text(le0$YEAR[16], le0$Females[16], le0$YEAR[16], pos=4)
abline(v = le0$YEAR[16], col=4)
text(le0$YEAR[32], le0$Females[32], le0$YEAR[32], pos=4)
abline(v = le0$YEAR[32], col=4)
axis(4, 80:88, as.character(seq(80-delta, 88-delta)))
legend("topleft", c("女", "男"), pch=c(19, 18), col=c(2, 1))
mtext("平均寿命　男", 4, 2)

Julia: 多重クロス集計表から元のデータフレームを復元する

「R による統計解析」の ５９ページにある「多重クロス集計表から元のデータフレームを復元する」を Julia で書いてみた。

julia> using DataFrames

julia> df = DataFrame(a = [1, 2, 3], b = ["a", "b", "c"], n = [2, 3, 4])
3×3 DataFrame
 Row │ a      b       n     
     │ Int64  String  Int64 
─────┼──────────────────────
   1 │     1  a           2
   2 │     2  b           3
   3 │     3  c           4

df の各行を df.n に書かれている数だけ水増しする（というのは聞こえが悪いので，元のデータセットを作ると言うかな）

空のデータフレームを作る。

julia> df2 = DataFrame()
0×0 DataFrame

作業本体

julia> for row in eachrow(df)
           for j in 1:row.n
               push!(df2, row)
           end
       end

できたかどうか見てみよう。

julia> df2
9×3 DataFrame
 Row │ a      b       n     
     │ Int64  String  Int64 
─────┼──────────────────────
   1 │     1  a           2
   2 │     1  a           2
   3 │     2  b           3
   4 │     2  b           3
   5 │     2  b           3
   6 │     3  c           4
   7 │     3  c           4
   8 │     3  c           4
   9 │     3  c           4

できてますね。

統計解析のためのJuliaの道具箱--1 固定書式ファイルをデータフレームに読み込む

"""
固定書式ファイルからデータフレームへ入力するプログラム

このプログラムを fixedformat.jl という名前で保存しておき，
使用するときに

include("fixedformat.jl")

でインクルードする。



使用法-1

fixedformat(fn; settype=true)

データファイルの 1, 2 行目に読み取り方を示す情報を記述しておく場合

データファイルの1行目に，カンマで区切った変数名
2行目には，読み込む変数の開始桁と変数の型を下記のように指定する
i は整数値 欄内に符号があってもよい
f は実数値 欄内に符号，小数点があってもよい
s は文字列
x は読み飛ばす
文字のある桁位置から次の文字のある桁位置の前までを文字の種類に応じて読む
以下の例では
1〜5   の 5 文字を整数値として読む
6〜13  の 8 文字を実数値として読む
14〜21 の 8 文字を文字列として読む
32〜35 の 4 文字を読み飛ばす...　ことを表している。
データは デフォルトでは 3 行目から
i1, f1, s1, i2, i3, f2
i    f       s       x   i i  f
1234567890123456789012345678901234567890
67897978.7827897289078329738290878696899
7897807890.80780780780780676786767967867

使用例-1-1

include("fixedformat.jl") # include はセッションごとに 1 回でよい
fn = "sample1.dat"
df = fixedformat(fn)

  i1: (i)  1 - 5 [5]
  f1: (f)  6 - 13 [8]
  s1: (s)  14 - 21 [8]
SKIP: (x)  22 - 25 [4]
  i2: (i)  26 - 27 [2]
  i3: (i)  28 - 30 [3]
  f2: (f)  31 - 39 [9]

4 rows × 6 columns

   i1     f1         s1        i2     i3     f2
   Int64  Float64    String    Int64  Int64  Float64
1  12345  6.78901e7  45678901  67     890    1.23457e8
2  67897  978.783    89728907  73     829    8.78697e7
3  78978  7890.8     78078078  67     678    6.76797e8

使用例-1-2

include("fixedformat.jl") # include はセッションごとに 1 回でよい
df = fixedformat(fn, settype=false)

settype=false を指定すると，各列の変数型を Any のままにする。

4 rows × 6 columns

   i1     f1         s1        i2   i3     f2
   Any    Any        Any       Any  Any    Any
1  12345  6.78901e7  45678901  67   890    1.23457e8
2  67897  978.783    89728907  73   829    8.78697e7
3  78978  7890.8     78078078  67   678    6.76797e8

使用法-2

include("fixedformat.jl") # include はセッションごとに 1 回でよい
fixedformat(fn; datarow=1, settype=true, names=String[], begins=Int[], ends=Int[], types=Char[])

変数名 names，開始桁位置 begins，終了桁位置 ends，変数の型 types をベクトルで与える場合

使用例-1 と同じことをするための関数呼び出しを例示する。
なお，上と同じデータファイルを使用する場合は，データの始まる行を datarow で指定しなければならない。
names は "name1" のようなダブルクオートで囲んだ文字列，types は 'i' のような文字型（シングルクオートで囲んだ一文字）で与えることに注意。

df = fixedformat(fn, datarow=3,
    names=["Int1", "Float1", "String", "Int2", "Int3", "Float2"],
    begins=[1, 6, 14, 26, 28, 31],
    ends=[5, 13, 21, 27, 30, 39],
    types=['i', 'f', 's', 'i', 'i', 'f'])

"""

using DataFrames
function getformat(format)
    begins = Int[]
    types  = Char[]
    for (b, t) in enumerate(format)
        isnothing(indexin(t, ['i', 'f', 's', 'x'])[1]) && continue
        append!(begins, b)
        append!(types,  t)
    end
    # println(begins)
    # println(types)
    ends = begins .- 1
    popfirst!(ends)
    push!(ends, length(format))
    (begins, ends, types)
end

function getdata(txt, begins, ends, types)
    data = Any[]
    for (b, e, t) in zip(begins, ends, types)
        if t == 'i'
            append!(data, parse(Int, txt[b:e]))
        elseif t == 'f'
            append!(data, parse(Float64, txt[b:e]))
        elseif t == 's'
            append!(data, [txt[b:e]])
        end
    end
    DataFrame(reshape(data, 1, :), :auto)
end

function fixedformat(fn; datarow=1, settype=true, names=String[], begins=Int[], ends=Int[], types=Char[])
    f = open(fn, "r")
    n = length(names)
    if n == 0
        names = split(readline(f), r"[, ]+")
        format = readline(f)
        # println(names)
        # println(format)
        (begins, ends, types) = getformat(format)
    else
        length(names) == length(begins) == length(ends) == length(types) || return "names, begins, ends, types の要素数が違います"
        for _ in 1:datarow-1
            readline(f)
        end
    end
    n = length(names)
    w = max(maximum(length.(names)), 5)
    j = 0
    for i in 1:length(begins)
        if types[i] != 'x'
            j += 1
            name = ((" " ^ (w)) * names[j])[end-w+1:end]
        else
            name = ((" " ^ (w)) * "SKIP")[end-w+1:end]
        end
        println("$name: ($(types[i]))  $(begins[i]) - $(ends[i]) [$(ends[i] - begins[i] + 1)]")
    end
    df = DataFrame[]
    while (txt = readline(f)) != ""
        if df == []
            df = getdata(txt, begins, ends, types)
            first = false
        else
            append!(df, getdata(txt, begins, ends, types))
        end
        # println(data)
    end
    close(f)
    rename!(df, names)
    settype || return df
    for i in 1:length(names)
        type = typeof(df[1, i])
        df[!, i] = type.(df[:, i])
        # println("$i, $type")
    end
    df
end

Julia で統計解析--その2 データの取扱

これらの文書群は github で管理することとした

最新バージョン 2022-02-02 16:45

以下を参照のこと

https://r-de-r.github.io/stats/Julia-stats2.html

1.　データをデータフレームへ読み込む
　1.1.　Excel のワークシートファイル
　1.2.　CSV ファイル
　　1.2.1.　典型的な CSV ファイル
　　1.2.2.　一般の CSV ファイル
　　1.2.3.　CSV.read の引数
　1.3. インターネット上の CSV ファイル
　1.4.　モニター上に表示された表をデータフレームに読み込む
　1.5.　クリップボードにコピーした内容をデータフレームにする
　1.6.　文字列行から入力する
　1.7.　エンコーディングの違うファイルを読む
　1.8.　デリミタで区切られていない固定書式ファイルを読む
2.　データフレームを CSV ファイルに書き出す
　2.1.　CSV.write の引数

さて，問題です。

以下の 35 枚の散布図で，相関係数が 0.63 のものはどれでしょうか?

答えは，ず〜〜〜〜〜とスクロール。

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

はい，全部です。全部，相関係数は正確に 0.63 です。

びっくりしましたか?

他の人にもこれを見せて意見を聞いてみましょう。

Julia で統計解析--その1 さあ，始めよう!！Julia

これらの文書群は github で管理することとした

最新バージョン 2022-01-26 22:55

以下を参照のこと

https://r-de-r.github.io/stats/Julia-stats1.html

1.　Julia を使ってみる
    1.1.　必要なファイルをダウンロードする
    1.2.　Julia のインストール
    1.3.　Julia を起動し終了する
    1.4.　作業ディレクトリを変える
    1.5.　Julia の環境設定をする
        1.5.1.　startup.jl ファイルがあるかを確認
        1.5.2.　config がなかった場合
        1.5.3.　startup.jl がある場合
        1.5.4.　変更内容の確認
1.6.　オンラインヘルプを使う
1.7.　パッケージを利用する
1.8.　エディタを使う
    1.8.1.　Atom
    1.8.2.　Jupyter lab
1.9.　結果を保存する

 

無駄をなくさないと速くならないこともある

前と同じようなプログラムになると思うと大間違いな場合。

平成 26 年度　京都数学オリンピック道場
10 桁の正の整数の各桁に 0 以上 9 以下のすべての整数が現れ，かつ 11111 の倍数であるとき，その整数を面白い整数と呼ぶことにする。面白い整数は全部でいくつあるか。

今回も「前と同じだ！」と，1 ずつ引いていくと大変なことになるのは目に見えているのに，

function func11()
    num = 9876543210
    cnt = 0
    for i in num:-1:1023456789
        if i%11111 == 0 && length(Set(string(i))) == 10
            cnt += 1
        end
    end
    print(cnt)
end
@time func11() # 3456  4.728315 seconds

ほらね。言ったとおりでしょ?
1 ずつ引く意味がないのに。

11111 ずつ引きましょう。

function func12()
    num = 9876543210 ÷ 11111 * 11111
    cnt = 0
    for i in num:-11111:1023456789
        length(Set(string(i))) == 10 && (cnt += 1)
    end
    print(cnt)
end
@time func12() # 3456  0.147158 seconds

無駄な引き算を繰り返さないので，30 倍速になりました。

なお，func11() があまりにも遅いので，「0~9 の順列を作って，数字を連結して数を作り，その数が 1000000000 より大きくて，かつ，11111 で割り切れる場合の数を数えよう」として，

using Combinatorics
function func13()
    cnt = 0
    a = collect(0:9)
    j = 0
    for i in 1:factorial(length(a))
        num = parse(Int, join(nthperm(a, i)))
        num > 1000000000 && num % 11111 == 0 && (cnt += 1)
    end
    println(cnt)
end

を呈示している。しかし，10! = 3628800 通りもの順列の数字を連結したりするのは結構時間がかかる。
しかも，そのうちの 10%（362880個）が 0 で始まる数なのでふるい落とさねばならない。

結局実行時間は

@time func13() # 3456  2.609802 seconds

という情けない結果になってしまう。

計算はたいして速くならないけど，無駄をなくす

2016年ジュニア数学オリンピック予選「各桁の数字が相異なるような３７の倍数のうち最大のものを求めよ。」

「10 桁の数の最大のものは 9876543210 なので，1ずつ引いてその数が37で割り切れ，かつ数字が相異なるか調べる」という戦略で，以下のようなプログラムが示されている。

function func1()
    num = 9876543210
    for i in num:-1:1
        if i%37 == 0 && length(Set(string(i))) == 10
            print(i)
            return
        end
    end
end

しかし，1 ずつ引いても，37 回目ごとにしか 37 の倍数にはならない。最大の 37 の倍数から始めて 37 ずつ引くのが妥当。大差はないが，塵も積もればということもあるから。

function func2()
    num = 9876543210 ÷ 37 * 37
    for i in num:-37:37
        length(Set(string(i))) == 10 && (println(i); return)
    end
end

Julia: プログラムを速くするための定石--その10

ヴィーフェリッヒ素数
http://commutative.world.coocan.jp/blog5/2020/11/post-182.html

関数化と Primes パッケージの isprime() を使うことによりほぼ 15 倍速となった。
元のプログラムと比較して欲しい。

using Primes
function Wiefelich()
    z = BigInt(1)
    k = BigInt(2)
    for p = 3:100000
        isprime(big(p)) && k^(p - 1) % (p^2) == 1 && print("$p ")
    end
end

@time Wiefelich()

1093 3511   0.069396 seconds (267.17 k allocations: 59.338 MiB, 3.79% gc time)

Julia: プログラムを速くするための定石--その9

Julia によるベルヌーイ数の計算
http://commutative.world.coocan.jp/blog5/2020/11/julia-3.html

factorual と binomial を自前の関数を書いているが，既存の関数（binomial だけでよい）を使うのが吉。

肝の Bernoulli 関数を以下のように書き換えた。
符号 s も元のプログラムでは (-1)^j としているがもったいない。

function Bernoulli(k::BigInt)
    B = Rational{BigInt}(0)
    for m = 0:k
        U = Rational{BigInt}(0)
        s = 1
        for j = 0:m
            U += s * binomial(m, j) * j^k
            s = -s
        end
        B += U // (m + 1)
    end
    B
end

元の Bernoulli(big(601)) は 93 秒ほどかかったが，書き換えたプログラムでは 0.6 秒で終わった。ほぼ 155 倍速になった。

この関数を 2〜1000 までの偶数に対して呼出す。奇数は 0//1 なので省略。
結果を出力すると余分な処理時間がかかる。

function f()
    for k = 2:2:1000
        #print("B_$k = ")
        b = Bernoulli2(big(k));
        #println(b)
    end;
end

@time f()

337.636791 seconds (4.57 G allocations: 327.160 GiB, 5.67% gc time)

Julia: ニュートン法により黄金比の値を 10000 桁求める

黄金比の値をニュートン法により小数点以下 n 桁まで求める。

function newton(n=10000)
    prec = floor(Int, n / log10(2))
    setprecision(prec+10)
    x = BigFloat(2)
    err = BigFloat(10)
    for i in 1:1000
        xn = (x^2+1) / (2x-1)
        i > 1 && string(xn)[end-5:end-1] == string(x)[end-5:end-1] && return ("converged", i, x)
        x = xn
    end
    ("not converged", 1000, x)
end

戻り値は，収束したかどうか，何回目のループか，整数部（1）を含む長精度での黄金比の値（BigBloat）の三組。

@time message, i, x = newton(10000); # 0.006522 seconds (692 allocations: 1.868 MiB)

ループ一回ごとに精度は倍になるので，10000 桁には 14 回で十分。

message, i # ("converged", 15)

出力関数は別に作った。

function printout(x; index=true)
    s = string(x)[3:end]
    println("  φ = 1.")
    for i in 1:50:length(s)
        i+49 > length(s) && break
        indx = index ? "$(("    " * string(i))[end-4:end]):" : ""
        println("$indx $(s[i:i+49])")
    end
end

printout(x)

 φ = 1.
    1: 61803398874989484820458683436563811772030917980576
   51: 28621354486227052604628189024497072072041893911374
  101: 84754088075386891752126633862223536931793180060766
  151: 72635443338908659593958290563832266131992829026788
  201: 06752087668925017116962070322210432162695486262963
                  :
 9901: 56345156390526577104264594760405569509598408889037
 9951: 62079956638801786185591594411172509231327977113803

http://k-ichikawa.blog.enjoy.jp/blog/2012/09/1-4ba1.html で確認したが，合っているようだ。

Julia: プログラムを速くするための定石--その8

ユークリッド－マリン数列
http://commutative.world.coocan.jp/blog5/2022/01/post-523.html

元のプログラムでは第 6 項の 50207 までなら 0.035977 秒で計算できる。しかし，第 7 項まで出そうとすると 1912.027524 秒かかる。しかも出てきた答え 547985393 は間違いである。

関数化，isprime()を使用するという小手先では 1887.464951 秒までしか縮まらずしかも出てくる答えは同じく 547985393 で間違いである。

計算のヒントは，元記事に「そもそも（第 7 項は）、340999 とあるけど、これは、2, 3, 7, 43, 139, 50207 をすべて掛け合わせて 1 を足した数である 12603664039 から、それの最大の素因数として求める」と書いてある。

また，数列のことならいつもの「オンライン整数列大辞典」ということで，検索してみると A000946 で，説明も同じ内容である。
Euclid-Mullin sequence: a(1) = 2, a(n+1) is largest prime factor of Product_{k=1..n} a(k) + 1.

元記事には続けて，「12603664039 から 340999 を求めること自体が大変なのだった」と書いているが，どれほど大変なのかプログラムを書いてみた。

using Primes

function Euclid_Mullin_sequence(limit=10)
    n = BigInt(2)
    println("1: $n")
    cum = n
    for i in 2:limit
        n = factor(Vector, cum + 1)[end]
        cum *= n
        println("$i: $n")
    end
end

関数の引数 limit を 2, 3, 4, ... と増やしていくと，順調に解が求まる。
第 7 項の 340999 までは 0.000345 秒
第 8 項の 2365347734339 までは 0.001223 秒
第 9 項の 4680225641471129 までは 0.322829 秒
第 10 項の 1368845206580129 までは 2.339921 秒
であったが，第 11 項まで求めようとすると相当時間がかかり一向に終わる気配がない。ので，諦めた。

第 11 項は
BigInt(2)*3*7*43*139*50207*340999*2365347734339*4680225641471129*1368845206580129 + 1
= 65127746440715056169703820896799129325103020802826145086639
の素因数分解をしなくてはならない。

高速計算といえば WolframAlpha であるが，流石に計算時間切れであった。

ということで，この問題を解く速いプログラムの定石は，
大変そうかもしれないが別の解法があるなら一応やってみる。
尤も，使える手段（関数）は惜しげなく使う。
かな。

@time Euclid_Mullin_sequence(10)

1: 2
2: 3
3: 7
4: 43
5: 139
6: 50207
7: 340999
8: 2365347734339
9: 4680225641471129
10: 1368845206580129
  1.611882 seconds (51.92 M allocations: 1.024 GiB, 24.76% gc time, 0.10% compilation time)

速いときには 2 秒を切ることもある。
@benchmark では最短 1.5 秒程度

Julia: プログラムを速くするための定石--その7

オイラーの級数
http://commutative.world.coocan.jp/blog5/2021/09/post-431.html

計算時間を短縮するには，関数化する，ファイル入力しないの他，今回は，

関数に実際に渡されるものに特化した関数定義，引数の精度を見極める。
同じものを何度も計算しない（関数を呼ばない），p^3, p^5 を毎回計算するのは無駄（特に長精度計算の場合）。

ということで，元のプログラムを以下のように書き換えた。

using Primes

function SGN(p) # p は奇数に限られる。 p は Int64 で十分
    if ((p - 1) ÷ 2) % 2 == 0
        return -1
    else
        return 1
    end
end

function h()
    S1 = S2 = S3 = 0
    for p0 in primes(3, 10^10) # 3 以上 10^10 未満の奇数素数が対象
        s = SGN(p0)
        p = Int128(p0)
        S1 += s / p
        p2 = p^2
        S2 += s / (p*p2)    # p^3, p^5 を別途計算するのは無駄
        S3 += s / (p*p2*p2)
    end
    println("Z(1) = $S1")
    println("Z(3) = $S2")
    println("Z(5) = $S3")
end
@time h()

Z(1) = 0.33498102728650697
Z(3) = 0.03225247383350187
Z(5) = 0.003858069415480658
 32.803606 seconds (87 allocations: 5.885 GiB, 0.02% gc time)

元のプログラムの実行時間は 1196.311773 秒だったので，40 倍速近い。
40 倍と言っても 20 分が 30 秒になるのは体感的に随分違う。

文字列の分数式を「分数式」に変換する

文字列として定義（入力）された "353//283286119" のような分数式 を Rational{BigInt} 353//283286119 に変換する。

function Str2Rat(line::String)
    p = 0
    AA = zero(BigInt)
    BB = zero(BigInt)
    for i = firstindex(line):lastindex(line)
        if line[i] == '/'
            p = i
        end
    end
    if p == 0
        A = line
        B = "1"
    else
        A = SubString(line, 1, p - 2)
        B = SubString(line, p + 1, lastindex(line))
    end
    AA = parse(BigInt, A)
    BB = parse(BigInt, B)
    return AA // BB
end

色々と知らない関数がたくさんあるが，仕様だけに基づいて次のように書き換えてみた。

function Str2Rat2(line::String)
    p = findfirst('/', line)
    if isnothing(p)
        parse(BigInt, line) // BigInt(1)
    else
        parse(BigInt, line[1:p - 1]) // parse(BigInt, line[p + 2:end])
    end
end

findfirst() は第1引数が第2引数中になければ nothing を返すことに注意。

両者が同じ結果を返すことを確認。

Str2Rat("13//37") == Str2Rat2("13//37") # true
Str2Rat("353")    == Str2Rat2("353")    # true

ベンチマークテストの結果は，後者は前者の2割ほど速いということだが，そもそも実行時間が 2,300 ns なので，どっちでもよい。
強いて言えば，後者のプログラムのほうがわかりやすいかな?という程度だ。

line="353//283286119"
using BenchmarkTools

t1 = @benchmark Str2Rat(line);
minimum(t1)

BenchmarkTools.TrialEstimate: 
  time:             310.467 ns
  gctime:           0.000 ns (0.00%)
  memory:           448 bytes
  allocs:           19

t2 = @benchmark Str2Rat2(line);
minimum(t2)

BenchmarkTools.TrialEstimate: 
  time:             251.522 ns
  gctime:           0.000 ns (0.00%)
  memory:           304 bytes
  allocs:           13

ちなみに，eval(Meta.parse(line)) でも同じ結果が得られるが，ns が μs になるレベルで，とても遅い。

t3 = @benchmark eval(Meta.parse(line));
minimum(t3)

BenchmarkTools.TrialEstimate: 
  time:             68.375 μs
  gctime:           0.000 ns (0.00%)
  memory:           1.95 KiB
  allocs:           42