正六角形の分割
締め切りが 2017/07/27 10:00 AM なので,その 1 分後に投稿されるように予約
正六角形があります。
正六角形の頂点と、辺の中点を全部合わせて「注目点」と呼びます。
注目点のうちいくつかを正六角形の中心と結んだ線分で、正六角形を分割します。
このとき、出来る図形が何角形なのかを計算して下さい。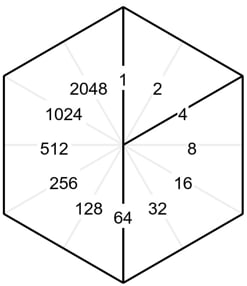
【入出力】
入力は
69
のようになっています。
これは、線分に割り当てられた値(右図参照)の合計です。
69=1 + 4 + 64
なので、上図の黒い線の部分で分割されます。
出力は、
3,4,4
のような感じです。
出来上がる多角形の頂点数を、昇順にコンマ区切りで。
【例】
入力 出力
69 3,4,4
57 3,3,4,6
1170 4,4,4,4
【補足】
・ 不正な入力に対処する必要はありません。
・ 少なくとも2箇所の注目点は、中心と結ばれます。
・ 内角が180度の点は頂点ではなく、辺の途中です。
・ 入力は 3以上 4095以下の整数です。
・ 凹多角形になっても気にせず頂点数を数えて下さい。
==================================
f = function(k) {
point = (1:32)[intToBits(k) == 1] # 選択される注目点の通し番号
n = length(point)
point = c(point, point[1] + 12) # 最後の要素は一回りした最初の注目点
count = NULL
for (i in 1:n) {
x = point[i]:point[i + 1]
m = length(x)
if (m > 2) {
for (j in 2:(m - 1)) {
if (x[j]%%2 == 0) { # 奇数番号目の注目点に挟まれる偶数番号目の注目点はカドにならない
x[j] = 0
}
}
}
count = c(count, (sum(x != 0) + 1 - (x[1] + 6 == x[m]))) # 最初と最後を結んで直線になれば 1 を引く
}
cat(paste(sort(count), collapse = ","))
}
> f(4095)
3,3,3,3,3,3,3,3,3,3,3,3
> f(3)
3,8
> f(5)
3,7
> f(10)
4,8
> f(260)
4,4
> f(520)
5,5
> f(132)
5,6
> f(1898)
3,3,3,3,4,4,4
> f(268)
3,4,5
> f(2176)
5,7
> f(1088)
4,6
> f(72)
4,7
Colorize 問題
締め切りが 2017/07/27 10:00 AM なので,その 1 分後に投稿されるように予約
ある検索ワードで、ある対象ワード群を検索し,各対象ワードが完全一致していたら黄色,部分一致していたら赤,にしてください。
色付けは以下の文法とします。
例えば hoge を黄色にするなら
[hoge]
hoge の ge を赤にするなら
ho=ge=
にしてください。
標準入力
・1行目は検索ワードです。[a-z]からなる1-10文字の文字列で構成されます。
・2行目は検索対象です。[a-z]からなる1-10文字の文字列がスペース区切りで与えられます。
スペースで区切られた各文字列を対象ワードと呼びます。
・対象ワードは1-5個入力されます。
例:
ge
hoge hige hege ge
標準出力
・対象ワード群を仕様に従って色付けした結果を出力してください
・検索ワードと対象ワードが完全一致した場合は該当対象ワードを黄色に色付けしてください
・検索ワードと対象ワードが部分一致した場合は該当対象ワードを赤に色付けしてください
・検索ワードにマッチしない箇所は色付けせずにそのまま出力してください
例(入力の例に対する出力の例)
ho=ge= hi=ge= he=ge= [ge]
その他の仕様
・標準入力の末尾には改行があります
・標準出力の末尾に改行をつけてください
・標準入力の仕様で説明した内容以外の入力は行われません(不正入力に対するチェックは不要)
Samples
Sample1
Input
hige
hoge hige hege
Output
hoge [hige] hege
Sample2
Input
ge
hoge hige hege
Output
ho=ge= hi=ge= he=ge=
Sample3
Input
ge
hoge hige hege ge
Output
ho=ge= hi=ge= he=ge= [ge]
=====================================
f = function(o, s) {
s = unlist(strsplit(s, " "))
for (i in seq_along(s)) {
if (s[i] == o) {
s[i] = sprintf("[%s]", o)
} else {
s[i] = gsub(o, sprintf("=%s=", o), s[i])
}
}
cat(paste(s, collapse=" "))
}
> f("ge", "hoge hige hege ge")
ho=ge= hi=ge= he=ge= [ge]
> f("hige", "hoge hige hege")
hoge [hige] hege
上下左右に箱を並べよう
締め切りが 2017/07/25 10:00 AM なので,その 1 分後に投稿されるように予約
設問
大手衣料品店のスマートフォンアプリとコラボレーションして話題になっている、ゲーム機での人気ゲームがあります。
(例えばこのようなゲームがイメージです→) http://www.uniqlo.com/jp/hacoboy/ ※CodeIQ外のサイトに飛びます。
このゲームのように、箱を並べるパターンが何通りあるかを求めることを考えます。
ここでは図のような格子状のマスにおいて、ある位置からスタートして、上下左右の隣り合う位置に箱を配置していきます。
すでに箱が配置されている位置、開始位置には箱を配置できません。
なお、上記のゲームでは最初に下方向に配置することはできませんが、本問では最初から下方向も可能とします。
配置する箱の数 n が与えられたとき、その箱の配置方法が何通りあるかを求めます。
ただし、できあがった位置と形だけで判断するものとし、その手順が異なっても同じ位置・同じ形であれば同じものとします。
例えば n = 3 のとき、以下のパターンはいずれも同じものとします。
n = 3 のとき、その箱の配置方法は以下の図のように上方向からスタートするものが9通り、そのほか全部で32通りがあります。
標準入力から n が与えられたとき、その箱の配置方法が何通りあるかを求め、標準出力に出力してください。
なお、n は 9以下の正の整数とします。
【入出力サンプル】
標準入力
3
標準出力
32
==========================================
R
quatrcombinations = function(p) {
retval = matrix(" ", nrow = 4^p, ncol = p)
for (n in 1:p) {
retval[, n] = rep(c(rep("U", 4^(p-n)), rep("D", 4^(p-n)), rep("L", 4^(p-n)),
rep("R", 4^(p-n))), length = 4^p)
}
retval
}
f = function(n) {
a = quatrcombinations(n)
size = 2*(n+1)-n%%2
result = NULL
apply(a, 1, function(p) {
board = matrix(0, size, size)
x = y = n+1
board[x, y] = 1
ok = TRUE
for (path in p) {
if (path == "U") {
y = y-1
} else if (path == "D") {
y = y+1
} else if (path == "L") {
x = x-1
} else {
x = x+1
}
if (board[x, y] == 1) {
ok = FALSE
break
}
board[x, y] = 1
}
if (ok == TRUE) {
rbind(result , c(board)) ->> result
}
})
cat(nrow(unique(result)))
}
system.time(f(6))
# f(1) # 4
# f(2) # 12
# f(3) # 32
# f(4) # 92
# f(5) # 248
# f(6) # 696
# f(7) # 1872
# f(8) # 5169
================================================
Java 8
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
long start = System.currentTimeMillis();
int i, j, k, l, n, size, w, zz;
if (true) {
n = 9; // 13876
} else {
Scanner cin = new Scanner(System.in);
String line;
line = cin.nextLine();
n = Integer.parseInt(line);
}
size = 2 * (n + 1) - n % 2;
int mx = (int) Math.pow(4, n);
int[][] result = new int[mx][n + 1];
int count = 0;
for (i = 0; i < mx; i++) {
zz = i;
int[][] board = new int[size][size];
int x, y;
x = y = n;
board[x][y] = 1;
boolean ok = true;
for (j = 0; j < n; j++) {
w = (int) (zz % 4);
zz = zz / 4;
if (w == 0) {
x++;
} else if (w == 1) {
x--;
} else if (w == 2) {
y++;
} else {
y--;
}
if (board[x][y] == 1) {
ok = false;
break;
}
board[x][y] = 1;
}
if (ok) {
int cnt = 0;
for (k = 0; k < size; k++) {
for (l = 0; l < size; l++) {
if (board[k][l] == 1) {
result[count][cnt++] = k * 10 + l;
}
}
}
count++;
}
}
int count2 = 0;
for (i = 0; i < count; i++) {
if (result[i][0] == -1) {
continue;
}
for (j = i + 1; j < count - 1; j++) {
boolean equal = true;
for (k = 0; n >= k; k++) {
if (result[i][k] != result[j][k]) {
equal = false;
break;
}
}
if (equal) {
result[j][0] = -1;
}
}
}
for (i = 0; i < count; i++) {
if (result[i][0] != -1) {
count2++;
}
}
System.out.println("count2 = " + count2);
long end = System.currentTimeMillis();
System.out.println((end - start) + "ms");
}
}
指定された回数で移動できる経路は何通り?
締め切りが 2017/07/18 10:00 AM なので,その 1 分後に投稿されるように予約
設問
横に m マス、縦に n マス並んだ格子状のマスがあり、
左上の隅から右下の隅までマスの周囲または対角線に沿って移動することを考えます。
ただし、対角線は左上から右下への線のみ可能とします。
(縦でも横でも斜めでも、いずれも1回で1マス分移動します)
移動は「右」「下」「右下」のいずれかとし、左や上、左上などに移動することはできません。
標準入力から m, n と合わせて移動回数 a がスペース区切りで与えられるとき、ちょうど a 回の移動で
右下の隅に到達する経路の数が何通りあるかを求め、標準出力に出力してください。
ただし、m, n は20以下の正の整数、a は m + n 以下の正の整数とします。
例えば、m = 3, n = 2, a = 3のとき、以下のような3通りが考えられます。
【入出力サンプル】
標準入力
3 2 3
標準出力
3
======================================================================
各ノードにおいて,次のノードへの移動法は 3 通り。
可能性のある径路は 3^a 通りあるが,そのうちには,枠外へはみ出したり,出口以外の枠内にとどまるものもある。
素直に数え上げるプログラムは以下の通りであるが,当然ながら,これでは a が大きくなると計算時間が掛かりすぎる。m=10, n=12, a=20 でも,無理である。
tricombinations = function(p) {
retval = matrix(" ", nrow = 3^p, ncol = p)
for (n in 1:p) {
retval[, n] = rep(c(rep("R", (3^p/3^n)), rep("D", (3^p/3^n)),
rep("F", (3^p/3^n))), length = 3^p)
}
retval
}
f = function(m, n, a) {
m = m+1
n = n+1
G = function(w) {
x = y = 1
for (i in seq_along(w)) {
if (w[i] != "D") {
x = x+1
}
if (w[i] != "R") {
y = y+1
}
if (board[x, y] == 2) {
return(i == a)
} else if (board[x, y] == 0) {
return(FALSE)
}
}
return(FALSE)
}
n1 = n+1
m1 = m+1
board = matrix(0, n1, m1)
board[1:n, 1:m] = 1
board[n, m] = 2
w = tricombinations(a)
sum(apply(w, 1, G))
}
f(3, 2, 3) # 3
f(4, 5, 6) # 60
#f(10, 12, 20)
#f(20, 20, 25)
f(15, 15, 10) # 0
別の方法を試みる。再帰プログラムであるが,メモ化する必要がある。
g(m, n, a) の解は,g(m-1, n, a-1) + g(m, n-1, a-1) + g(m-1, n-1, a-1) により求められる。
f = function(m, n, a) {
m = m+1 # 横方向のノード数
n = n+1 # 縦方向のノード数
memo = array(-1, dim = c(m, n, a))
g = function(m, n, a) {
if (m < 1 || n < 1) {
return(0)
}
if (memo[m, n, a] != -1) {
return(memo[m, n, a])
}
if (a < max(m, n)-1 || a > m + n - 2) {
0 ->> memo[m, n, a]
return(0)
} else if ((m == 1 && n == 2 && a == 1) || (m == 2 && n == 1 && a == 1)) {
1 ->> memo[m, n, a]
return(1)
} else if (m == 2 && n == 2 && a == 1) {
1 ->> memo[m, n, a]
return(1)
} else if (m == 2 && n == 2 && a == 2) {
2 ->> memo[m, n, a]
return(2)
} else {
g(m - 1, n, a - 1) + g(m, n - 1, a - 1) + g(m - 1, n - 1, a - 1) ->> memo[m, n, a]
}
memo[m, n, a]
}
cat(g(m, n, a), "\n")
}
#s = scan(file("stdin", "r"), quiet=TRUE)
#f(s[1], s[2], s[3])
system.time({ # 0.062 sec.
f(3, 2, 3) # 3
f(4, 5, 6) # 60
f(10, 12, 20) # 8314020
f(20, 20, 25) # 823727520
f(15, 15, 10) # 0
})
数字が最大のマインスイーパ
締め切りが 2017/7/11 10:00 AM なので,その 1 分後に投稿されるように予約
Windows のゲームとして有名なマインスイーパ。
長方形のマスの中に地雷が埋まっており、その隣接するマスに書かれている数字を元に、地雷の場所を特定します。
このとき、隣接するというのは、上下左右だけでなく、斜めの位置も含みます。
なお、地雷があるマスに数字が書かれることはありません。
m × n のマスの中に a 個の地雷が配置されている場合を考えます。
このとき、このマスの中に書かれている数字の和の最大値を求めます。
例えば、m = 4, n = 4, a = 3 のとき、以下の「*」の位置に地雷を配置すると、数字の和の最大値は19となります。
標準入力から m, n, a がスペース区切りで与えられたとき、その数字の和の最大値を求め、標準出力に出力してください。
なお、m, n, a はいずれも正の整数で、m × n ≦ 28、 a ≦ 4 を満たすものとします。
【入出力サンプル】
標準入力
4 4 3
標準出力
19
================================================
R では時間制限に引っかかる。
f = function(m, n, a) {
g = function(y) {
z = matrix(0, m, n)
z[y] = 1
w = matrix(0, m + 2, n + 2)
w[1:m + 1, 1:n + 1] = z
s = 0
for (i in 1:m + 1) {
for (j in 1:n + 1) {
if (w[i, j] == 0) {
s = s +sum(w[i+(-1:1), j+(-1:1)])
}
}
}
s
}
mn = m * n
s = combn(mn, a, g)
cat(max(s))
}
system.time(f(3, 3, 2)) # 11, 0.035 sec.
system.time(f(4, 4, 3)) # 19, 0.017 sec.
system.time(f(5, 5, 4)) # 32, 0.540 sec.
system.time(f(4, 7, 4)) # 30, 1.004 sec.
system.time(f(3, 9, 4)) # 32, 0.872 sec.
Java で書いて OK
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
if (false) {
System.out.println(f(3, 3, 2));
System.out.println(f(4, 4, 3));
System.out.println(f(5, 5, 4));
System.out.println(f(4, 7, 4));
System.out.println(f(3, 9, 4));
} else {
int m, n, a;
Scanner cin = new Scanner(System.in);
String line;
line = cin.nextLine();
String[] line2 = line.split(" ");
m = Integer.parseInt(line2[0]);
n = Integer.parseInt(line2[1]);
a = Integer.parseInt(line2[2]);
System.out.println(f(m, n, a));
}
}
static int f(int m, int n, int a) {
int[][] z = new int[m + 2][n + 2];
int i, j;
int[] y = new int[a + 1];
int[] x = new int[m * n + 1];
for (i = 1; m * n >= i; i++) {
x[i] = i;
}
int[][] ind = combn(x, m * n, a);
int s = 0;
for (j = 1; j < ind[0].length; j++) {
for (i = 1; a >= i; i++) {
y[i] = ind[i][j] - 1;
}
s = Math.max(s, g(y, m, n));
}
return s;
}
static int g(int[] y, int m, int n) {
int i, j, ix, iy;
int[][] w = new int[m + 2][n + 2];
for (i = 1; i < y.length; i++) {
ix = (y[i] % m) + 1;
iy = (int) (y[i] / m) + 1;
w[ix][iy] = 1;
}
int s = 0;
for (i = 1; i < m + 1; i++) {
for (j = 1; j < n + 1; j++) {
if (w[i][j] == 0) {
s = s + w[i - 1][j - 1] + w[i][j - 1] + w[i + 1][j - 1]
+ w[i - 1][j] + w[i + 1][j] + w[i - 1][j + 1]
+ w[i][j + 1] + w[i + 1][j + 1];
}
}
}
return s;
}
static double factorial(int n) {
int i;
double result = 1;
for (i = 1; n >= i; i++) {
result *= i;
}
return result;
}
static int[][] combn(int[] x, int n, int m) {
int e, h, i, j, nmmp1, lenr;
int[] a = new int[m + 1];
int[] r = new int[m + 1];
int count = (int) (factorial(n) / factorial(m) / factorial(n - m));
int[][] out = new int[m + 1][count + 1];
e = 0;
h = m;
for (i = 1; m >= i; i++) {
a[i] = i;
r[i] = x[i];
}
lenr = r.length - 1;
for (j = 1; count >= j; j++) {
for (i = 1; lenr >= i; i++) {
out[i][j] = r[i];
}
}
i = 2;
nmmp1 = n - m + 1;
while (a[1] != nmmp1) {
if (e < n - h) {
h = 1;
e = a[m];
} else {
e = a[m - h];
h++;
}
for (j = 1; h >= j; j++) {
a[m - h + j] = e + j;
}
for (j = 1; m >= j; j++) {
out[j][i] = x[a[j]];
}
i++;
}
return out;
}
}
同じ形に分割
締め切りが 2017/07/04 10:00 AM なので,その 1 分後に投稿されるように予約
設問
横 m マス、縦 n マスの長方形があります。これを同じ形の2つの領域に分割することを考えます。
ただし、それぞれの領域はすべて縦・横でつながっている(隣り合っている)ものとします。
つまり、同じ色の領域が複数に分かれてはいけませんし、斜めの場合は隣り合っているとはみなしません。
分割する位置はマスの区切りとし、斜めに分割したり、1つのマスを複数に分けたりすることはできません。
また、分割する線の位置を決めるものとし、色が逆のパターンは1つとカウントします。
なお、「同じ形」とは点対称のように回転させて重なる形とします。
例えば、m = 4, n = 3のブロックの場合、以下の左にあるような9通りの分け方があります。
右のような分け方は、つながっていないためNGです。
標準入力から m と n がスペース区切りで与えられたとき、何通りの分け方があるかを求め、
その数を標準出力に出力してください。
なお、m, n はともに正の整数で、 1 < m × n < 25 を満たすものとします。
【入出力サンプル】
標準入力
3 4
標準出力
9
============================================
R では時間制限をクリアできない
F = function(n, m) {
G = function(x) {
board = matrix(-1, n + 2, m + 2)
board[1:n + 1, 1:m + 1] = matrix(x, n, m)
ij = which(board == 1, arr.ind = TRUE)[1, ]
board[ij[1], ij[2]] = 2
repeat {
ij = which(board == 2, arr.ind = TRUE)
change = FALSE
for (k in seq_len(nrow(ij))) {
i = ij[k, 1]
j = ij[k, 2]
if (board[i - 1, j] == 1) {
change = TRUE
board[i - 1, j] = 2
}
if (board[i + 1, j] == 1) {
change = TRUE
board[i + 1, j] = 2
}
if (board[i, j - 1] == 1) {
change = TRUE
board[i, j - 1] = 2
}
if (board[i, j + 1] == 1) {
change = TRUE
board[i, j + 1] = 2
}
}
if (change == FALSE) {
break
}
}
return(all(board != 1))
}
H = function(x) {
x = matrix(x, n, m)
return(all(x + x[n:1, m:1] == 1))
}
bincombinations = function(p) {
retval = matrix(0, nrow = 2^p, ncol = p)
for (n in 1:p) {
retval[, n] = rep(rep(0:1, each = 2^(p - n)), length = 2^p)
}
retval
}
mn = m * n
if (mn%%2 == 1) {
return(0)
}
mn2 = mn/2
a = cbind(0, bincombinations(mn - 1)) # 半分だけ調べればよい
b = rowSums(a) == mn2 # 同じ色のセル数が等しいか
c = a[b, ]
d = apply(c, 1, H) # 同じ形か
e = c[d, ]
f = apply(e, 1, G) # 縦横でつながっているか
g = e[f, ]
cat(nrow(g))
}
system.time(F(4, 4)) # 22, 0.211 sec.
system.time(F(3, 4)) # 9, 0.137 sec.
system.time(F(2, 8)) # 8, 0.055 sec.
system.time(F(4, 5)) # 39, 1.177 sec.
F(3, 7) # 0
system.time(F(4, 6)) # 90, 12.406 sec.
===========================================
Java 7 は遅いが,Java 8 で OK
import java.util.Scanner;
public class SameShape {
public static void main(String[] args) {
if (false) {
long start = System.currentTimeMillis();
System.out.println(F(4, 4)); // 22
System.out.println(F(3, 4)); // 9
System.out.println(F(2, 8)); // 8
System.out.println(F(4, 5)); // 39
System.out.println(F(3, 7)); // 0
System.out.println(F(4, 6)); // 90
long end = System.currentTimeMillis();
System.out.println((end - start) + "ms");
} else {
Scanner cin = new Scanner(System.in);
String line;
line = cin.nextLine();
String [] line2 = line.split(" ");
int n = Integer.parseInt(line2[0]);
int m = Integer.parseInt(line2[1]);
System.out.println(F(n, m));
}
}
static int F(int n, int m) {
int mn = m * n;
if ((int) mn % 2 == 1) {
return 0;
}
int mn2 = mn / 2;
int i, j, p;
int[] y = new int[mn];
int color;
int count = 0;
for (i = (int) Math.pow(2, mn2) - 1; i < Math.pow(2, mn - 1); i += 2) {
p = i;
color = 0;
for (j = 0; j < mn; j++) {
y[j] = p & 0x00000001;
if (y[j] == 1) {
++color;
}
p >>= 1;
}
if (color == mn2 && G(y, n, m)) {
count++;
}
}
return count;
}
static boolean G(int[] x, int n, int m) {
int[][] board = new int[n + 2][m + 2];
int i, j, k = 0;
int xLength = x.length;
for (i = 0; i < xLength / 2; i++) {
if (x[i] + x[xLength - 1 - i] != 1)
return false;
}
for (i = 1; n >= i; i++) {
for (j = 1; m >= j; j++) {
board[i][j] = x[k++];
}
}
for (i = 1; n >= i; i++) {
for (j = 1; m >= j; j++) {
if (board[i][j] + board[n + 1 - i][m + 1 - j] != 1)
return false;
}
}
boolean flag = false;
for (i = 1; n >= i; i++) {
for (j = 1; m >= j; j++) {
if (board[i][j] == 1) {
board[i][j] = 2;
flag = true;
break;
}
}
if (flag) {
break;
}
}
for (;;) {
int count = 0;
boolean change = false;
int[] ii = new int[24];
int[] jj = new int[24];
for (i = 1; n >= i; i++) {
for (j = 1; m >= j; j++) {
if (board[i][j] == 2) {
ii[count] = i;
jj[count] = j;
count++;
}
}
}
for (k = 0; k < count; k++) {
i = ii[k];
j = jj[k];
if (board[i - 1][j] == 1) {
change = true;
board[i - 1][j] = 2;
}
if (board[i + 1][j] == 1) {
change = true;
board[i + 1][j] = 2;
}
if (board[i][j - 1] == 1) {
change = true;
board[i][j - 1] = 2;
}
if (board[i][j + 1] == 1) {
change = true;
board[i][j + 1] = 2;
}
}
if (change == false) {
break;
}
}
for (i = 1; n >= i; i++) {
for (j = 1; m >= j; j++) {
if (board[i][j] == 1) {
return false;
}
}
}
return true;
}
}



















