算額(その215)
中村信弥「改訂増補 長野県の算額」
http://www.wasan.jp/zoho/zoho.html
県内の算額2(134)
長野県長野市元善町 善光寺 天保3年(1832)
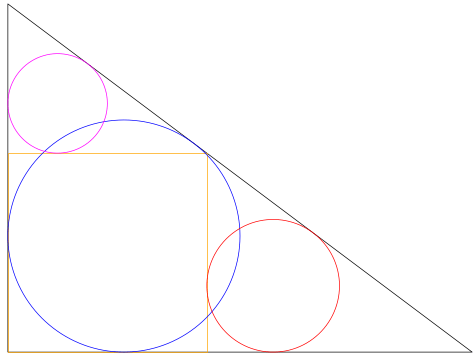
鉤股の中に正方形,全円,中円,小円が入っている。3 個の円の径の和の 3 乗に鉤股弦の3辺の和を加えると 175784 寸になるとき,鉤,股の長さを求めよ。
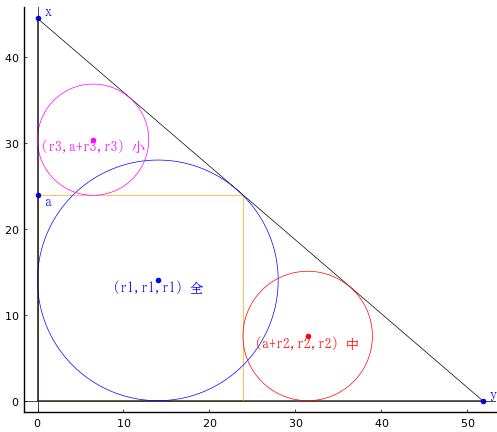
全円,中円,小円の半径を r1, r2, r3,正方形の一辺の長さを a とする。a = r1*(1 + 1/√2)
鉤,股,弦の長さを x, y, z とする。z^2 = x^2 + y^2
using SymPy
@syms r1::positive, r2::positive, r3::positive, a::positive, x::positive, y::positive, z::positive;
鉤股弦に内接する円の直径に関する公式により
eq1 = (x + y - z) - 2r1
鉤股弦の定理により
eq2 = x^2 + y^2 - z^2eq3 = r1*(1 + 1/√Sym(2)) - a
中円が内接する直角三角形において,鉤 = a,股 = y - a,より弦を求め,更に中円の径を求める。
eq4 = a + (y - a) - sqrt(a^2 + (y - a)^2) - 2r2
小円が内接する直角三角形において,鉤 = x - a,股 = a,より弦を求め,更に小円の径を求める。
eq5 = (x - a) + a - sqrt((x - a)^2 + a^2) - 2r3
eq6 = sqrt(a^2 + (y - a)^2) + sqrt((x - a)^2 + a^2) - z
3 円の径の 3 乗と鉤股弦の長さの和が 175784 寸になること。
eq7 = (2r1 + 2r2 + 2r3)^3 + (x + y + z) - 175784
# res = solve([eq1, eq2, eq3, eq4, eq5, eq6, eq7], (r1, r2, r3, a, x, y, z))
println(eq1, ",")
println(eq2, ",")
println(eq3, ",")
println(eq4, ",")
println(eq5, ",")
println(eq6, ",")
println(eq7, ",")
-2*r1 + x + y - z,
x^2 + y^2 - z^2,
-a + r1*(sqrt(2)/2 + 1),
-2*r2 + y - sqrt(a^2 + (-a + y)^2),
-2*r3 + x - sqrt(a^2 + (-a + x)^2),
-z + sqrt(a^2 + (-a + x)^2) + sqrt(a^2 + (-a + y)^2),
x + y + z + (2*r1 + 2*r2 + 2*r3)^3 - 175784,
nlsolve() に与える初期値として,以下では [14, 8, 6, 24, 42, 56, 70] を与えている。これが何であるかは,後ほど明らかにする。
using NLsolve
function nls(func, params...; ini = [0.0])
if typeof(ini) <: Number
r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=1e-14)
v = r.zero[1]
else
r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=1e-14)
v = r.zero
end
return v, r.f_converged
end;
function H(u)
(r1, r2, r3, a, x, y, z) = u
return [
-2*r1 + x + y - z,
x^2 + y^2 - z^2,
-a + r1*(sqrt(2)/2 + 1),
-2*r2 + y - sqrt(a^2 + (-a + y)^2),
-2*r3 + x - sqrt(a^2 + (-a + x)^2),
-z + sqrt(a^2 + (-a + x)^2) + sqrt(a^2 + (-a + y)^2),
x + y + z + (2*r1 + 2*r2 + 2*r3)^3 - 175784,
]
end;
iniv = [big"14.0", 8, 6, 24, 42, 56, 70]
res = nls(H, ini=iniv);
(r1, r2, r3, a, x, y, z) = res[1]
7-element Vector{BigFloat}:
14.00009199718881266997164505667248631437239191211784047768957946446283538592614
7.530673092915759606828706615206250886849777022685165021155300562153373379538257
6.469418904767690724808290956523842847260715462871629533555945388717614860294677
23.89965205591648493671409981825858528719421105627886838770965718274749524331951
44.47523941973287034607539732539475983162747384861150323437216124063871614521499
51.79378645760826848096196046976934542743851611350476010640996323602390734022659
68.26890380908048029730932373318754118070670892490859464615855881182802342371832
この結果は,条件式を満たすがその制度は低い。
residuals = [-2*r1 + x + y - z,
x^2 + y^2 - z^2,
-a + r1*(sqrt(2)/2 + 1),
-2*r2 + y - sqrt(a^2 + (-a + y)^2),
-2*r3 + x - sqrt(a^2 + (-a + x)^2),
-z + sqrt(a^2 + (-a + x)^2) + sqrt(a^2 + (-a + y)^2),
x + y + z + (2*r1 + 2*r2 + 2*r3)^3 - 175784];
residuals
7-element Vector{BigFloat}:
-6.192611696681021525605136840855038550278702801226075559326409107071012901001753e-05
9.765402982411353192658777533349762286583446730354184844530409424450095677342936e-06
-7.027994826461461300837844291342422836735678351587353901813809597787233631272473e-08
-5.355063501058776092617519186570005715143107383625329191134445449929575796103538e-05
-5.608181214456910119933111617475016179932686281639492614172558048509090495266509e-05
4.7705340913023316164424824417060357246824030732233419126833127607968720315658e-05
-4.706396192122615236089639278606438686047887003738046689427877440546358609517795e-08
得られたパラメータで図に描いてみれば,誤差は気にならない。
r1 = 14.00009; r2 = 7.53067; r3 = 6.46942; a = 23.89965; x = 44.47524; y = 51.79379; z = 68.26890
(2r1 + 2r2 + 2r3)^3 + (x + y + z) = 175784.00000

using Plots
using Printf
function circle(ox, oy, r, color=:red; beginangle=0, endangle=360)
θ = beginangle:0.1:endangle
x = r.*cosd.(θ)
y = r.*sind.(θ)
plot!(ox .+ x, oy .+ y, color=color, linewidth=0.5)
end;
function point(x, y, string="", color=:blue, position=:left, vertical=:top; mark=true)
mark && scatter!([x], [y], color=color, markerstrokewidth=0)
annotate!(x, y, text(string, 10, position, color, vertical))
end;
function draw(more)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(r1, r2, r3, a, x, y, z) = res[1]
@printf("r1 = %.5f; r2 = %.5f; r3 = %.5f; a = %.5f; x = %.5f; y = %.5f; z = %.5f\n", r1, r2, r3, a, x, y, z)
@printf("(2r1 + 2r2 + 2r3)^3 + (x + y + z) = %.5f\n", (2r1 + 2r2 + 2r3)^3 + (x + y + z))
plot([0, y, 0, 0], [0, 0, x, 0], color=:black, lw=0.5)
plot!([0, a, a, 0, 0], [0, 0, a, a, 0], color=:orange, lw=0.5)
circle(r1, r1, r1, :blue)
circle(a + r2, r2, r2, :red)
circle(r3, a + r3, r3, :magenta)
if more == true
point(r1, r1, "(r1,r1,r1) 全", :blue, :center)
point(a + r2, r2, "(a+r2,r2,r2) 中", :red, :center)
point(r3, a + r3, "(r3,a+r3,r3) 小", :magenta, :center)
point(0, a, " a")
point(0, x, " x", :blue, :left, :bottom)
point(y, 0, " y", :blue, :left, :bottom)
hline!([0], color=:black, lw=0.5)
vline!([0], color=:black, lw=0.5)
else
plot!(showaxis=false)
end
end;
draw(true)
savefig("fig1.png");
そもそも,算額の結果は整数解あるいはきれいな式で表されるのが普通なので,数値解を見てみると r1 が整数に近いこと,a は r1 ほどではないが整数値に近い。
r1 = 14 が算額における真値であると仮定する。鉤股弦に内接する円の径の方程式 eq1 = (x + y - z) - 2r1 より x + y - z = 28。
また当然 eq2 = x^2 + y^2 - z^2。
これを解くのに SymPy はちょっと力不足。
@syms x::positive, y::positive, z::positive;
eq1 = x + y - z - 28
eq2 = x^2 + y^2 - z^2;
1 ≦ x ≦ y ≦ 1000 で条件を満たすものはそんなに多くはない。
for x in 1:1000
for y in x:1000
z = round(Int, sqrt(x^2 + y^2))
if x^2 + y^2 == z^2 && x + y - z == 28
println("(x, y, z) = ($x, $y, $z) GCD(x, y, z) = $(gcd(x, y, z))")
end
end
end
(x, y, z) = (29, 420, 421) GCD(x, y, z) = 1
(x, y, z) = (30, 224, 226) GCD(x, y, z) = 2
(x, y, z) = (32, 126, 130) GCD(x, y, z) = 2
(x, y, z) = (35, 84, 91) GCD(x, y, z) = 7
(x, y, z) = (36, 77, 85) GCD(x, y, z) = 1
(x, y, z) = (42, 56, 70) GCD(x, y, z) = 14
馴染みの深いのが (x, y, z) = (42, 56, 70) なので,これと当たりをつけて先に進む。
(x, y, z) = (42, 56, 70)
r1 = (x + y - z)/2 # 14
r1 |> println
14.0
a = r1*(1 + 1/√2) # eq3
a |> println
23.899494936611664
これにより得られた a は数値解に近く,更に,ほぼ 24 であるのが好ましい。a = 24 にしよう。
更に,中円,小円の半径は (a + (y - a) - sqrt(a^2 + (y - a)^2))/2,((x - a) + a - sqrt((x - a)^2 + a^2) - 2r3)/2 である。
a = 24
r2 = (a + (y - a) - sqrt(a^2 + (y - a)^2)) / 2
r3 = ((x - a) + a - sqrt((x - a)^2 + a^2)) / 2
(r2, r3) |> println
(8.0, 6.0)
(2r1 + 2r2 + 2r3)^3 + (x + y + z) # 問に合う
175784.0
図に描いても,a = 24 としたことによる誤差(斜辺と円接点が正方形の角になるべき)のはあまり目立たない。
function draw2()
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(r1, r2, r3, a, x, y, z) = [14, 8, 6, 24, 42, 56, 70]
@printf("r1 = %.5f; r2 = %.5f; r3 = %.5f; a = %.5f; x = %.5f; y = %.5f; z = %.5f\n", r1, r2, r3, a, x, y, z)
@printf("(2r1 + 2r2 + 2r3)^3 + (x + y + z) = %.5f\n", (2r1 + 2r2 + 2r3)^3 + (x + y + z))
plot([0, y, 0, 0], [0, 0, x, 0], color=:black, lw=0.5)
plot!([0, a, a, 0, 0], [0, 0, a, a, 0], color=:orange, lw=0.5)
circle(r1, r1, r1, :blue)
circle(a + r2, r2, r2, :red)
circle(r3, a + r3, r3, :magenta)
plot!(showaxis=false)
end;
draw2()
savefig("fig3.png");
r1 = 14.00000; r2 = 8.00000; r3 = 6.00000; a = 24.00000; x = 42.00000; y = 56.00000; z = 70.00000
(2r1 + 2r2 + 2r3)^3 + (x + y + z) = 175784.00000