算額(その496)
岐阜県郡上市八幡町 八幡神社 嘉永3年(1850)
早坂平四郎: 算額の一考察,苫小牧工業専門学校紀要
https://www.tomakomai-ct.ac.jp/wp01/wp-content/uploads/2014/06/kiyou5-8.pdf
外円内に半径の等しい 6 個の大円が入っている。小円は外円の同心円で,この 6 個の大円に外接する。2個の大円に外接し外円に内接する円を甲円,2個の大円と小円に外接する円を乙円とする。
甲円と乙円の直径が与えられたとき,外円の直径を求めよ。
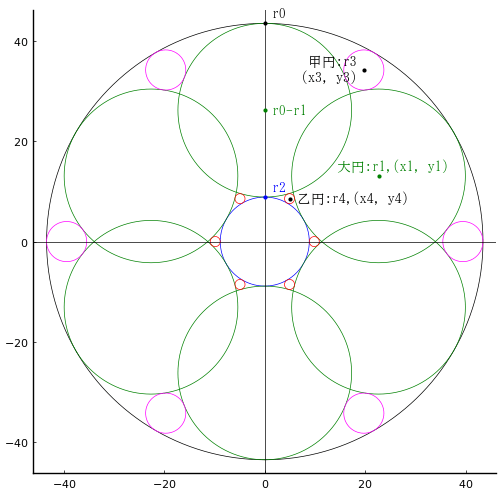
外円の半径と中心座標を r0, (0, 0)
大円の半径と中心座標を r1, (0, r0 - r1), (x1, y1)
小円の半径と中心座標を r2, (0, 0); r2 = r0 - 2r1
甲円の半径と中心座標を r3, (x3, y3)
乙円の半径と中心座標を r4, (x4, y4)
として,以下の連立方程式を解く。
include("julia-source.txt");
using SymPy
@syms r0::positive, r1::positive, r2::positive,
r3::positive, r4::positive;
@syms r0, r1, r2, r3, r4
r2 = r0 - 2r1
x1 = (r0 - r1)cosd(Sym(30))
y1 = (r0 - r1)sind(Sym(30))
x3 = (r0 - r3)cosd(Sym(60))
y3 = (r0 - r3)sind(Sym(60))
x4 = (r2 + r4)cosd(Sym(60))
y4 = (r2 + r4)sind(Sym(60))
eq1 = (x1 - x3)^2 + (y1 - y3)^2 - (r1 + r3)^2
eq2 = (x1 - x4)^2 + (y1 - y4)^2 - (r1 + r4)^2
res = solve([eq1, eq2], (r0, r1))
2-element Vector{Tuple{Sym, Sym}}:
((-sqrt(-16*r3*r4*(-15*sqrt(3)*r3 + 26*r3 - 15*sqrt(3)*r4 + 26*r4)^2 + (-31*sqrt(3)*r3^2 + 54*r3^2 - 58*sqrt(3)*r3*r4 + 100*r3*r4 - 31*sqrt(3)*r4^2 + 54*r4^2)^2)/(4*(-26*r3 + 15*sqrt(3)*r3 - 26*r4 + 15*sqrt(3)*r4)) + (-31*sqrt(3)*r3^2 + 54*r3^2 - 58*sqrt(3)*r3*r4 + 100*r3*r4 - 31*sqrt(3)*r4^2 + 54*r4^2)/(4*(-15*sqrt(3)*r3 + 26*r3 - 15*sqrt(3)*r4 + 26*r4)))*(-56*sqrt(3)*r3^2 + 97*r3^2 - 1448*sqrt(3)*r3*r4 + 2508*r3*r4 - 1616*sqrt(3)*r4^2 + 2799*r4^2 + (-sqrt(-16*r3*r4*(-15*sqrt(3)*r3 + 26*r3 - 15*sqrt(3)*r4 + 26*r4)^2 + (-31*sqrt(3)*r3^2 + 54*r3^2 - 58*sqrt(3)*r3*r4 + 100*r3*r4 - 31*sqrt(3)*r4^2 + 54*r4^2)^2)/(4*(-26*r3 + 15*sqrt(3)*r3 - 26*r4 + 15*sqrt(3)*r4)) + (-31*sqrt(3)*r3^2 + 54*r3^2 - 58*sqrt(3)*r3*r4 + 100*r3*r4 - 31*sqrt(3)*r4^2 + 54*r4^2)/(4*(-15*sqrt(3)*r3 + 26*r3 - 15*sqrt(3)*r4 + 26*r4)))*(-2702*r3 + 1560*sqrt(3)*r3 - 2702*r4 + 1560*sqrt(3)*r4))/(-1351*r3^2 + 780*sqrt(3)*r3^2 - 780*sqrt(3)*r4^2 + 1351*r4^2), -sqrt(-16*r3*r4*(-15*sqrt(3)*r3 + 26*r3 - 15*sqrt(3)*r4 + 26*r4)^2 + (-31*sqrt(3)*r3^2 + 54*r3^2 - 58*sqrt(3)*r3*r4 + 100*r3*r4 - 31*sqrt(3)*r4^2 + 54*r4^2)^2)/(4*(-26*r3 + 15*sqrt(3)*r3 - 26*r4 + 15*sqrt(3)*r4)) + (-31*sqrt(3)*r3^2 + 54*r3^2 - 58*sqrt(3)*r3*r4 + 100*r3*r4 - 31*sqrt(3)*r4^2 + 54*r4^2)/(4*(-15*sqrt(3)*r3 + 26*r3 - 15*sqrt(3)*r4 + 26*r4)))
((sqrt(-16*r3*r4*(-15*sqrt(3)*r3 + 26*r3 - 15*sqrt(3)*r4 + 26*r4)^2 + (-31*sqrt(3)*r3^2 + 54*r3^2 - 58*sqrt(3)*r3*r4 + 100*r3*r4 - 31*sqrt(3)*r4^2 + 54*r4^2)^2)/(4*(-26*r3 + 15*sqrt(3)*r3 - 26*r4 + 15*sqrt(3)*r4)) + (-31*sqrt(3)*r3^2 + 54*r3^2 - 58*sqrt(3)*r3*r4 + 100*r3*r4 - 31*sqrt(3)*r4^2 + 54*r4^2)/(4*(-15*sqrt(3)*r3 + 26*r3 - 15*sqrt(3)*r4 + 26*r4)))*(-56*sqrt(3)*r3^2 + 97*r3^2 - 1448*sqrt(3)*r3*r4 + 2508*r3*r4 - 1616*sqrt(3)*r4^2 + 2799*r4^2 + (sqrt(-16*r3*r4*(-15*sqrt(3)*r3 + 26*r3 - 15*sqrt(3)*r4 + 26*r4)^2 + (-31*sqrt(3)*r3^2 + 54*r3^2 - 58*sqrt(3)*r3*r4 + 100*r3*r4 - 31*sqrt(3)*r4^2 + 54*r4^2)^2)/(4*(-26*r3 + 15*sqrt(3)*r3 - 26*r4 + 15*sqrt(3)*r4)) + (-31*sqrt(3)*r3^2 + 54*r3^2 - 58*sqrt(3)*r3*r4 + 100*r3*r4 - 31*sqrt(3)*r4^2 + 54*r4^2)/(4*(-15*sqrt(3)*r3 + 26*r3 - 15*sqrt(3)*r4 + 26*r4)))*(-2702*r3 + 1560*sqrt(3)*r3 - 2702*r4 + 1560*sqrt(3)*r4))/(-1351*r3^2 + 780*sqrt(3)*r3^2 - 780*sqrt(3)*r4^2 + 1351*r4^2), sqrt(-16*r3*r4*(-15*sqrt(3)*r3 + 26*r3 - 15*sqrt(3)*r4 + 26*r4)^2 + (-31*sqrt(3)*r3^2 + 54*r3^2 - 58*sqrt(3)*r3*r4 + 100*r3*r4 - 31*sqrt(3)*r4^2 + 54*r4^2)^2)/(4*(-26*r3 + 15*sqrt(3)*r3 - 26*r4 + 15*sqrt(3)*r4)) + (-31*sqrt(3)*r3^2 + 54*r3^2 - 58*sqrt(3)*r3*r4 + 100*r3*r4 - 31*sqrt(3)*r4^2 + 54*r4^2)/(4*(-15*sqrt(3)*r3 + 26*r3 - 15*sqrt(3)*r4 + 26*r4)))
2組の解が得られるが,最初のものが適解である。
甲円,乙円の直径が 8, 2 のとき,外円の直径は約 86.9559 である。
外円の直径 = 86.9559; r0 = 43.4779; r1 = 17.3042; r2 = 8.86948; r3 = 4, r4 = 1
using Plots
function draw(more)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(r3, r4) = (8, 2) .// 2
(r0, r1) = ((-sqrt(-16*r3*r4*(-15*sqrt(3)*r3 + 26*r3 - 15*sqrt(3)*r4 + 26*r4)^2 + (-31*sqrt(3)*r3^2 + 54*r3^2 - 58*sqrt(3)*r3*r4 + 100*r3*r4 - 31*sqrt(3)*r4^2 + 54*r4^2)^2)/(4*(-26*r3 + 15*sqrt(3)*r3 - 26*r4 + 15*sqrt(3)*r4)) + (-31*sqrt(3)*r3^2 + 54*r3^2 - 58*sqrt(3)*r3*r4 + 100*r3*r4 - 31*sqrt(3)*r4^2 + 54*r4^2)/(4*(-15*sqrt(3)*r3 + 26*r3 - 15*sqrt(3)*r4 + 26*r4)))*(-56*sqrt(3)*r3^2 + 97*r3^2 - 1448*sqrt(3)*r3*r4 + 2508*r3*r4 - 1616*sqrt(3)*r4^2 + 2799*r4^2 + (-sqrt(-16*r3*r4*(-15*sqrt(3)*r3 + 26*r3 - 15*sqrt(3)*r4 + 26*r4)^2 + (-31*sqrt(3)*r3^2 + 54*r3^2 - 58*sqrt(3)*r3*r4 + 100*r3*r4 - 31*sqrt(3)*r4^2 + 54*r4^2)^2)/(4*(-26*r3 + 15*sqrt(3)*r3 - 26*r4 + 15*sqrt(3)*r4)) + (-31*sqrt(3)*r3^2 + 54*r3^2 - 58*sqrt(3)*r3*r4 + 100*r3*r4 - 31*sqrt(3)*r4^2 + 54*r4^2)/(4*(-15*sqrt(3)*r3 + 26*r3 - 15*sqrt(3)*r4 + 26*r4)))*(-2702*r3 + 1560*sqrt(3)*r3 - 2702*r4 + 1560*sqrt(3)*r4))/(-1351*r3^2 + 780*sqrt(3)*r3^2 - 780*sqrt(3)*r4^2 + 1351*r4^2), -sqrt(-16*r3*r4*(-15*sqrt(3)*r3 + 26*r3 - 15*sqrt(3)*r4 + 26*r4)^2 + (-31*sqrt(3)*r3^2 + 54*r3^2 - 58*sqrt(3)*r3*r4 + 100*r3*r4 - 31*sqrt(3)*r4^2 + 54*r4^2)^2)/(4*(-26*r3 + 15*sqrt(3)*r3 - 26*r4 + 15*sqrt(3)*r4)) + (-31*sqrt(3)*r3^2 + 54*r3^2 - 58*sqrt(3)*r3*r4 + 100*r3*r4 - 31*sqrt(3)*r4^2 + 54*r4^2)/(4*(-15*sqrt(3)*r3 + 26*r3 - 15*sqrt(3)*r4 + 26*r4)))
r2 = r0 - 2r1
x1 = (r0 - r1)cosd(30)
y1 = (r0 - r1)sind(30)
x3 = (r0 - r3)cosd(60)
y3 = (r0 - r3)sind(60)
x4 = (r2 + r4)cosd(60)
y4 = (r2 + r4)sind(60)
@printf("外円の直径 = %g; r0 = %g; r1 = %g; r2 = %g; r3 = %g, r4 = %g\n", 2r0, r0, r1, r2, r3, r4)
plot()
circle(0, 0, r0, :black)
circle(0, 0, r2, :blue)
rotate(0, r0 - r1, r1, :green, angle=60)
rotate(r0 - r3,0, r3, :magenta, angle=60)
rotate(r2 + r4, 0, r4, :red, angle=60)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:black, lw=0.5)
vline!([0], color=:black, lw=0.5)
point(0, r0, " r0", :black, :left, :bottom, delta=delta/2)
point(0, r2, " r2", :blue, :left, :bottom, delta=delta/2)
point(0, r0 - r1, " r0-r1", :green, :left, :vcenter)
point(x1, y1, " 大円:r1,(x1, y1)", :green, :center, :bottom, delta=delta/2)
point(x3, y3, "甲円:r3 \n(x3, y3) ", :black, :right, :vcenter)
point(x4, y4, " 乙円:r4,(x4, y4) ", :black, :left, :vcenter)
else
plot!(showaxis=false)
end
end;




























