算額（その254）

算額（その254）

中村信弥「改訂増補 長野県の算額」
http://www.wasan.jp/zoho/zoho.html
県内の算額4（199)
長野県北佐久郡軽井沢町峠 熊野神社 安政4年(1857)

角錐台に大球と小球が外接して入っている。小球は上面，大球は下面に接し，それぞれは4つの側面にも外接している。上面，下面の正方形の一辺がそれぞれ 125寸，2000寸のとき，小球の直径を求めよ。

側面方向からの透視図を描くと，図に示すように等脚台形の中に大小の円が入っていることになる。

大円の半径と中心座標を r2, (0, r2)
小円の半径と中心座標を r1, (0, 2r2 + r1)
それぞれの円の中心から台形の脚への距離について，以下の連立方程式を解く。

include("julia-source.txt");

using SymPy

@syms r1::positive, r2::positive, a::positive, b::positive;

a = 125//2
b = 2000//2
eq1 = distance(a, 2r2+2r1, b, 0, 0, 2r2 + r1) - r1^2
eq2 = distance(a, 2r2+2r1, b, 0, 0, r2) - r2^2
res = solve([eq1, eq2], (r1, r2))

   1-element Vector{Tuple{Sym, Sym}}:
    (125, 500)

小球の直径は 2 × 125 = 250寸，大球の直径は 2 × 500 = 1000寸

a, b を変数のまま連立方程式を解くと，r1, r2 は a, b を含む式になる。

using SymPy

@syms r1::positive, r2::positive, a::positive, b::positive;

# a = 125//2
# b = 2000//2
eq1 = distance(a, 2r2+2r1, b, 0, 0, 2r2 + r1) - r1^2
eq2 = distance(a, 2r2+2r1, b, 0, 0, r2) - r2^2
res = solve([eq1, eq2], (r1, r2))

   1-element Vector{Tuple{Sym, Sym}}:
    (a^(3/4)*b^(1/4), a^(7/4)*b^(3/4)*(-sqrt(a) + sqrt(b))/(a^(3/2)*sqrt(b) - a^2))

r1 = a^(3/4)*b^(1/4)
r2 = a^(7/4)*b^(3/4)*(-sqrt(a) + sqrt(b))/(a^(3/2)*sqrt(b) - a^2)
それぞれを求める関数を以下のようにする。

f_r1(a, b) = a^(3/4)*b^(1/4);
f_r2(a, b) = a^(7/4)*b^(3/4)*(-sqrt(a) + sqrt(b))/(a^(3/2)*sqrt(b) - a^2);

f_r1(big"125"/2, big"2000"/2)*2

   250.0

f_r2(big"125"/2, big"2000"/2)*2

   1000.0

なお，術では，小球の直径 = sqrt(a * sqrt(a * b)) であるがこれは，上述の a^(3/4) * b^(1/4) に等しい。

@syms a::positive, b::positive;
sqrt(a * sqrt(a * b))|> simplify |> println

   a^(3/4)*b^(1/4)

using Plots
using Printf

function draw(more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r1, r2) = (125, 500)
   plot([1000, 125/2, -125/2, -1000, 1000], [0, 2r1 + 2r2, 2r1 + 2r2, 0, 0], linecolor=:black, linewidth=0.5)
   circle(0, 2r2 + r1, r1)
   circle(0, r2, r2, :blue)
   if more == true
       point(0, r2, " r2", :blue)
       point(0, 2r2 + r1, " 2r2+r1", :red)
       point(125/2, 2r1 + 2r2, " (125/2,2r1+2r2)", :black)
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
   else
      plot!(showaxis=false)
   end
end;

算額（その253）

算額（その253）

中村信弥「改訂増補 長野県の算額」
http://www.wasan.jp/zoho/zoho.html
県内の算額4（199)
長野県北佐久郡軽井沢町峠 熊野神社 安政4年(1857)

鉤股弦において，鉤と股の積が 52440 平方寸，股と弦の積が 130065 平方寸のとき，鉤，股，弦それぞれの長さを求めよ。

以下の連立方程式を解く。

include("julia-source.txt");

using SymPy

@syms 鉤::positive, 股::positive, 弦::positive;

eq1 = 鉤 * 股 - 52440
eq2 = 股 * 弦 - 130065
eq3 = 鉤^2 + 股^2 - 弦^2
res = solve([eq1, eq2, eq3], (鉤, 股, 弦))

   1-element Vector{Tuple{Sym, Sym, Sym}}:
    (152, 345, 377)

鉤 = 152, 股 = 345, 弦 = 377 である。

using Plots
using Printf

function draw(more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (鉤, 股, 弦) = (152, 345, 377)
   plot([0, 股, 0, 0], [0, 0, 鉤, 0], linecolor=:black, linewidth=0.5)
   if more == true
       point(0, 鉤/2, " 鉤 = 152寸", :green, :left, :bottom, mark=false)
       point(股/2, 0, " 股 = 345寸", :blue, :center, :bottom, mark=false)
       point(股/2, 鉤/2, " 弦 = 377寸", :red, :left, :bottom, mark=false)
   else
      plot!(showaxis=false)
   end
end;

算額（その252）

算額（その252）

中村信弥「改訂増補 長野県の算額」
http://www.wasan.jp/zoho/zoho.html
県内の算額3（234)
長野県北佐久郡軽井沢町峠 熊野神社 明治5年(1872)

円内の弦の上に等円 2 個と菱形が入っている。菱形の長い方の対角線の長さが 8 寸，等円の径が 4 寸，のとき図の「矢」の長さはいかほどか。

外円の半径，中心座標を r0, (0, r1) とする。
弦の位置の y 座標を y とする。「矢」の長さは y である。
右側の等円の半径，中心座標を r1, (r1, y + r1) とする。r1 = 2 である。
菱形の短い方の対角線の長さを 2b とおく。b = 4 である。
菱形の短い方の対角線の長さを 2a とおく。菱形の右の頂点は (4, 2r0 - a) である。

以下の連立方程式を解く。

include("julia-source.txt");

using SymPy

@syms r0::positive, r1::positive, a::positive, b::positive, y::positive;

r1 = 2
b = 4
eq1 = b^2 +(r0 - a)^2 - r0^2
eq2 = r1^2 + (r0 - r1 - y)^2 - (r0 - r1)^2
eq3 = distance(0, 2r0 - 2a, b, 2r0 - a, r1, y + r1) - r1^2;
eq3 = (distance(0, 2r0 - 2a, b, 2r0 - a, r1, y + r1) - r1^2)*(a^2 + b^2)/b |> expand |> simplify;
res = solve([eq1, eq2, eq3], (r0, a, y))

   3-element Vector{Tuple{Sym, Sym, Sym}}:
    (9/2, 9/2 - sqrt(17)/2, 1)
    (9/2, sqrt(17)/2 + 9/2, 1)
    (9*sqrt(5)/5, 2*sqrt(5), 1 + 3*sqrt(5)/5)

(9/2, 9/2 - sqrt(17)/2, 1) |> println
(9/2, sqrt(17)/2 + 9/2, 1) |> println
(9*sqrt(5)/5, 2*sqrt(5), 1 + 3*sqrt(5)/5) |> println

   (4.5, 2.4384471871911697, 1)
   (4.5, 6.561552812808831, 1)
   (4.024922359499621, 4.47213595499958, 2.341640786499874)

a < b なので，最初の解が適切である。

このとき「矢」は 1，もとの単位では 1 寸である。

   r0 = 4.5000000;  a = 2.4384472;  y（矢） = 1.0000000

SymPy の solve() では，r1, b を変数のままで r0, a, y を求めることはできない (計算時間が長く一向に終わらない）。

術では，等円^2 / 4(菱長 - 等円) である。

func(r1, b) = 2(r1^2//4(b - r1))

func(2, 4), func(3, 7), func(2, 7), func(1, 6)

   (1//1, 9//8, 2//5, 1//10)

using Plots

function draw(more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r0, a, y) = res[1]
   @printf("r0 = %.7f;  a = %.7f;  y（矢） = %.7f\n", r0, a, y)
   r1 = 2
   x = 4
   plot([x, 0, -x, 0, x], [2r0 - a, 2r0, 2r0 - a, 2r0 - 2a, 2r0 - a], color=:black, lw=0.5)
   circle(0, r0, r0)
   circle(r1, y + r1, r1, :blue)
   circle(-r1, y + r1, r1, :blue)
   x1 = sqrt(r0^2 - (r0 - y)^2)
   segment(-x1, y, x1, y)
   if more == true
       point(0, 2r0, " 2r0", :red, :left, :bottom)
       segment(-4, 2r0 - a, 4, 2r0 - a)
       point(0, 2r0 - a, " 2r0-a", :black)
       point(0, 2r0 - 2a, " 2r0-2a", :black)
       point(0, r0, " r0", :red)
       point(0, y, " y", :black)
       point(r1, y + r1, "(r1,y+r1)", :blue)
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
   else
       plot!(showaxis=false)
   end
end;

算額（その251）

算額（その251）

中村信弥「改訂増補 長野県の算額」
http://www.wasan.jp/zoho/zoho.html
県内の算額3（234)
長野県北佐久郡軽井沢町峠 熊野神社 明治5年(1872)

長方形の中に 12 個の円が入っている。乙円の径が 1 寸のとき，甲円の径を求めよ。

(-x,0), (x, y) を対角とする長方形の右半分を対象にする。
等円の半径，中心座標を r1, (x - r1, r) とする。y = 2r1 である。
甲円の半径，中心座標を r2, (x2, r2) とする。
乙円の半径，中心座標を r3, (0, r3) とする。
丙円の半径，中心座標を r4, (x4, r4) とする。
丁円の半径，中心座標を r5, (0, y - r5) とする。
戊円の半径，中心座標を r6, (x6, y - r6) とする。
無名円の半径，中心座標を r7, (x7, y7) とする。

以下の連立方程式を解く。

include("julia-source.txt");

r3 は変数のままで，nlsolve() を使うときに定義する。

using Printf
using NLsolve

function nls(func, params...; ini = [0.0])
   if typeof(ini) <: Number
       r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=1e-14)
       v = r.zero[1]
   else
       r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=1e-14)
       v = r.zero
   end
   return v, r.f_converged
end;

function H(u)
   (r1, x, r2, x2, r4, x4, r5, r6, x6, r7, x7, y7) = u
   return [
       (r1 - r2)^2 - (r1 + r2)^2 + (-r1 + x - x2)^2,  # eq1
       (-r1 + r6)^2 - (r1 + r6)^2 + (-r1 + x - x6)^2,  # eq2
       -(r2 + r6)^2 + (x2 - x6)^2 + (-2*r1 + r2 + r6)^2,  # eq3
       (r2 - r4)^2 - (r2 + r4)^2 + (x2 - x4)^2,  # eq4
       x4^2 + (r3 - r4)^2 - (r3 + r4)^2,  # eq5
       x7^2 - (r3 + r7)^2 + (r3 - y7)^2,  # eq6
       -(r2 + r7)^2 + (r2 - y7)^2 + (x2 - x7)^2,  # eq7
       x6^2 + (r5 - r6)^2 - (r5 + r6)^2,  # eq8
       x2^2 - (r2 + r5)^2 + (2*r1 - r2 - r5)^2,  # eq9
       x7^2 - (r5 + r7)^2 + (2*r1 - r5 - y7)^2,  # eq10
       -(r4 + r7)^2 + (r4 - y7)^2 + (x4 - x7)^2,  # eq11
       -r1 + r3 + r5,  # eq12
   ]
end;

r3 = 0.5
iniv = [big"1.5", 5.45, 0.9, 1.6, 0.22,　0.69,　1,　0.7,　1.8,　0.18,　0.5,　0.9]
res = nls(H, ini=iniv);

names = ["r1", "x", "r2", "x2", "r4", "x4", "r5", "r6", "x6", "r7", "x7", "y7"]
for i in 1:length(names)
   @printf("%2s = %.7f\n", names[i], res[1][i])
end
println("収束した? ",res[2])

   r1 = 1.8419829
    x = 6.4757422
   r2 = 1.0000000
   x2 = 1.9193660
   r4 = 0.3160343
   x4 = 0.7950274
   r5 = 1.3419829
   r6 = 0.8482252
   x6 = 2.1338263
   r7 = 0.2631404
   x7 = 0.6619656
   y7 = 0.8797167
   収束した? true

甲円の半径は r2 = 1 よって，もとの単位では甲円の直径は 2 寸である。

using Plots

function circlesym(x, y, r, c)
   circle(x, y, r, c)
   circle(-x, y, r, c)
end;

function draw(more)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r1, x, r2, x2, r4, x4, r5, r6, x6, r7, x7, y7) = res[1]
   y = 2r1
   plot([-x, x, x, -x, -x], [0, 0, y, y, 0], color=:black, lw=0.5)
   circlesym(x - r1, r1, r1, :red)
   circle(0, r3, r3, :blue)
   circle(0, 2r3 + r5, r5, :green)
   circlesym(x4, r4, r4, :brown)
   circlesym(x6, y - r6, r6, :magenta)
   circlesym(x2, r2, r2, :blue)
   circlesym(x7, y7, r7, :red)
   if more == true
       point(x - r1, r1, " 等円\n (x-r1,r1)", :red, :left, :bottom)
       point(x2, r2, " 甲円\n (x2,r2)", :blue, :left, :bottom)
       point(x6, y - r6, " 戊円\n (x6,y-r6)\n", :magenta, :center, :bottom)
       point(0, y - r5, " 丁円\n y-r5", :green, :left, :bottom)
       point(0, r3, " 乙円\n r3", :blue, :left, :bottom)
       point(x4, r4, "  丙円\n    (x4,r4)", :brown, :left, :bottom)
       point(x7, y7, "   (x7,y7)", :red, :left, :bottom)
       point(x, 0, "x ", :black, :right, :bottom)
       point(0, y, " y", :black, :left, :top)
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5, xlims=(-0.1,6.6))
   else
       plot!(showaxis=false)
   end
end;

算額（その250）

算額（その250）

中村信弥「改訂増補 長野県の算額」
http://www.wasan.jp/zoho/zoho.html
県内の算額3（234)
長野県北佐久郡軽井沢町峠 熊野神社 明治5年(1872)

外円の弦の上に 9 個の円が入っている。等円の径が 1 寸のとき，外円の径はいかほどか。

弦と y 軸の交点の座標を (0, y) とする。 
外円の半径，中心座標を r0, (0, 0) とする。
等円の半径，中心座標を r1, (x1, y + r1) とする。
右の下円の半径，中心座標を r2, (x2, y + r2) とする。
中央の下円の半径，中心座標を r2, (0, y + r2) とする。
上円の半径，中心座標を r3, (0, r0 - r3) とする。
上円と下円に挟まれる3個の円のうち，
   右側の円の半径，中心座標を r4, (x4, r4) とする。
   中央の円の半径，中心座標を r5, (0, r0 - 2r3 - r5) とする。

以下の関数 H(u) 中の連立方程式を解く。

r1 は変数のままで，nlsolve() を使うときに定義する。

include("julia-source.txt");

using Printf
using NLsolve

function nls(func, params...; ini = [0.0])
   if typeof(ini) <: Number
       r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=1e-14)
       v = r.zero[1]
   else
       r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=1e-14)
       v = r.zero
   end
   return v, r.f_converged
end;

function H(u)
   (r0, x1, r2, x2, r3, r4, x4, y4, r5, y) = u
   return [
       x2^2 - (r0 - r2)^2 + (r2 + y)^2,  # eq1
       (r1 - r2)^2 - (r1 + r2)^2 + (x1 - x2)^2,  # eq2
       x1^2 - (r0 - r1)^2 + (r1 + y)^2,  # eq3
       -(r1 + r4)^2 + (x1 - x4)^2 + (r1 + y - y4)^2,  # eq4
       x1^2 - (r1 + r3)^2 + (-r0 + r1 + r3 + y)^2,  # eq5
       x4^2 - (r4 + r5)^2 + (r0 - 2*r3 - r5 - y4)^2,  # eq6
       x1^2 + (r1 - r2)^2 - (r1 + r2)^2,  # eq7
       x4^2 - (r2 + r4)^2 + (-r2 - y + y4)^2,  # eq8
       x4^2 - (r3 + r4)^2 + (r0 - r3 - y4)^2,  # eq9
       -r0 + 2*r2 + 2*r3 + 2*r5 + y,  # eq10
   ]
end;

r1 = 0.5
iniv = [big"2.1", 0.69, 0.24, 1.39, 0.29, 0.07, 0.12, 1.36, 0.05, 0.83]
res = nls(H, ini=iniv);

names = ["r0", "x1", "r2", "x2", "r3", "r4", "x4", "y4", "r5", "y"]
for i in 1:length(names)
   @printf("%2s = %.7f\n", names[i], res[1][i])
end
println("収束した? ",res[2])

   r0 = 2.0000000
   x1 = 0.6966214
   r2 = 0.2426407
   x2 = 1.3932428
   r3 = 0.2928932
   r4 = 0.0736862
   x4 = 0.1239249
   y4 = 1.3621096
   r5 = 0.0502525
    y = 0.8284271
   収束した? true

外円の半径は r0 = 2.0，元の単位で直径は 4 寸である。

using Plots

function draw(more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r0, x1, r2, x2, r3, r4, x4, y4, r5, y) = res[1]
   @printf("r0 = %.5f\n", r0)
   plot()
   x = sqrt(r0^2 - y^2)
   segment(x, y, -x, y)
   circle(0, 0, r0, :black)
   circle(x1, y + r1, r1)
   circle(-x1, y + r1, r1)
   circle(x2, y + r2, r2, :blue)
   circle(-x2, y + r2, r2, :blue)
   circle(0, y + r2, r2, :blue)
   circle(0, r0 - r3, r3, :green)
   circle(0, y + 2r2 + r5, r5, :red)
   circle(x4, y4, r4, :black)
   circle(-x4, y4, r4, :black)
   if more == true
       point(x1, y + r1, "(x1,y+r1)", :red, :center, :top)
       point(x2, y + r2, "(x2,y+r2)", :blue, :center, :top)
       point(0, r0, "(0,r0)", :black, :left, :bottom)
       point(0, y, "(0,y)", :black, :left, :top)
       point(x, y, "(x,y)", :black, :left, :top)
       point(0, r0 - r3, "r0-r3", :green)
       point(0, y + r2, "y+r2", :green)
       plot!([0, -1.2r1], [y + 2r2 + r5, r0], line=(:arrow, :red, 0.5))
       point(-1.2r1, r0, "(0,y+2r+r5)", :red, :right, :bottom, mark=false)
       # segment(x4, y4, 1.5, r0, :black)
       plot!([x4, 1.2r1], [y4, r0], line=(:arrow, :black, 0.5))
       point(1.2r1, r0, "(x4,y4)", :black, :left, :bottom, mark=false)
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
   else
       plot!(showaxis=false)
   end
end;

 

算額（その248）

算額（その248）

中村信弥「改訂増補 長野県の算額」
http://www.wasan.jp/zoho/zoho.html
県内の算額3（229)
長野県諏訪市下諏訪 諏訪大社下社 慶応4年(1868)

長方形内に大円 1 個，中円，小円がそれぞれ 4 個入っている。大円の径が 1 寸のとき，長方形の長辺の長さはいかほどか。

長方形の長辺，短辺の長さをそれぞれ x，y とする。
第 1 象限の図形を対象とする。
大円の中心を原点とする。
大円の半径，中心座標を r1, (0, 0) とする。y = 2r1 である。
中円の半径，中心座標を r2, (x/2 - r2, y/2 - r2) とする。
小円の半径，中心座標を r3, (x/2 - r3, r3) とする。

問では「大円の径が 1 寸のとき」としているが，術では大円と長方形の長辺の関係を述べているので，以下では r1 も変数として連立方程式を解く。解は，r1 を含む式になる。

include("julia-source.txt");

using SymPy

@syms r1::positive, r2::positive, r3::positive,
   x::positive, y::positive;

r1 = 1//2
y = 2r1
eq1 = (x/2 - r2)^2 + (y/2 - r2)^2 - (r1 + r2)^2
eq2 = (x/2 - r3)^2 + r3^2 - (r1 + r3)^2
eq3 = (r2 - r3)^2 + (y/2 - r2 - r3)^2 - (r2 + r3)^2;

res = solve([eq1, eq2, eq3], [r2, r3, x])

   1-element Vector{Tuple{Sym, Sym, Sym}}:
    (4*sqrt(2)*r1/49 + 9*r1/49, 4*r1*(11 - 6*sqrt(2))/49, 2*r1*(23/49 + 32*sqrt(2)/49))

r1 = 0.5 とすると

   r1 = 0.50000;  r2 = 0.14956;  r3 = 0.10264;  x = 1.39296;  y = 1.00000

長辺の長さは 1.39296 である。

x は 2\*r1\*(23/49 + 32\*sqrt(2)/49) である。2r1 は大円の直径（径）であるので， x は 大円の径の (23//49 + 32\*sqrt(Sym(2))/49) 倍である。

2*r1*(23//49 + 32*sqrt(Sym(2))/49) |> simplify |> println

   2*r1*(23 + 32*sqrt(2))/49

術は「2048 の平方根に，23 を加え，大円の径を掛けて，49 で割る」

(sqrt(Sym(2048)) + 23) * 2r1 / 49 |> println

   2*r1*(23 + 32*sqrt(2))/49

同じである。

using Plots
using Printf

function draw(more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r1 = 1/2
   y = 2r1
   (r2, r3, x) = (4*sqrt(2)*r1/49 + 9*r1/49, 4*r1*(11 - 6*sqrt(2))/49, 2*r1*(23/49 + 32*sqrt(2)/49))
   @printf("r1 = %.5f;  r2 = %.5f;  r3 = %.5f;  x = %.5f;  y = %.5f\n", r1, r2, r3, x, y)
   plot([x/2, x/2, -x/2, -x/2, x/2], [-y/2, y/2, y/2, -y/2, -y/2], color=:black, lw=0.5)
   circle(0, 0, r1)
   circle4(x/2 - r2, y/2 - r2, r2, :blue)
   circle4(x/2 - r3, r3, r3, :green)
   if more == true
       point(0, 0, " 大円", :red, :left, :bottom)
       point(x/2 - r2, y/2 - r2, "中円", :blue, :left)
       point(x/2 - r3, r3, "小円", :green, :left)
       point(x/2, y/2, "(x/2,y/2)", :black, :right, :bottom)
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
   else
       plot!(showaxis=false)
   end
end;

算額（その247）

算額（その247）

中村信弥「改訂増補 長野県の算額」
http://www.wasan.jp/zoho/zoho.html
県内の算額3（229)
長野県諏訪市下諏訪 諏訪大社下社 慶応4年(1868)

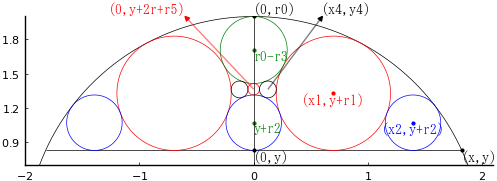
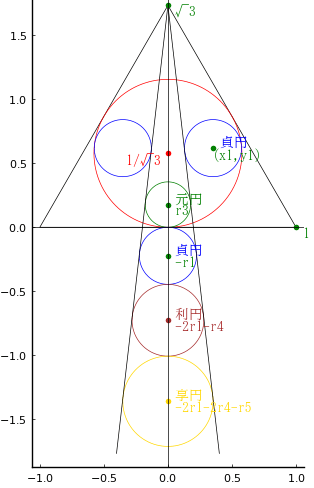
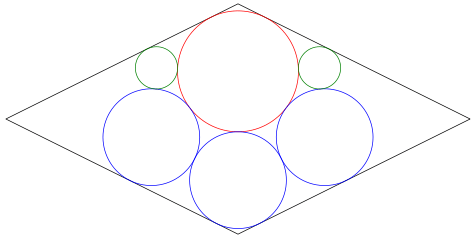
菱形の中に日円，月円，星円がそれぞれ 1 個，3 個，2 個入っている。
日円，月円の径を知って，星円の径を求めよ。

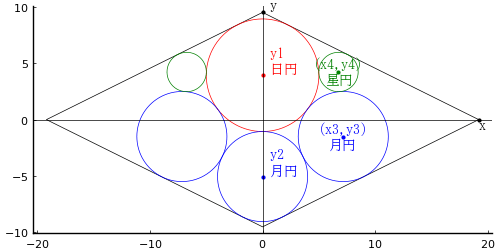
菱形の中心を原点とする。x 軸上の頂点の x 座標を x，y 軸上の頂点の y 座標を y とする。
日円の半径，中心座標を r1, (0, y1) とする。
真ん中の月円の半径，中心座標を r2, (0, y2) とする。
右の月円の半径，中心座標を r3, (x3, y3) とする。r3 = r2 である。
星円の半径，中心座標を r4, (x4, r4) とする。

以下の連立方程式を解く。

include("julia-source.txt");

using SymPy

@syms r1::positive, y1::positive, r2::positive, y2::negative,
   r3::positive, x3::positive, y3::positive,
   r4::positive, x4::positive, y4::positive,
   x::positive, y::positive;

r3 = r2
eq1 = x4^2 + (y1 - y4)^2 - (r1 + r4)^2
eq2 = (x3 - x4)^2 + (y3 - y4)^2 - (r3 + r4)^2
eq3 = x3^2 + (y1 - y3)^2 - (r1 + r3)^2
eq4 = x3^2 + (y2 - y3)^2 - (r2 + r3)^2
eq5 = distance(0, y, x, 0, 0, y1) - r1^2
eq6 = distance(0, y, x, 0, x4, y4) - r4^2
eq7 = distance(0, -y, x, 0, 0, y2) - r2^2
eq8 = distance(0, -y, x, 0, x3, y3) - r3^2
eq9 = (sqrt(x^2 + y^2)/x + 1) * (r1 + r2) - 2y;

# solve([eq1, eq2, eq3, eq4, eq5, eq6, eq7, eq8, eq9])

println(eq1, ",  # eq1")
println(eq2, ",  # eq2")
println(eq3, ",  # eq3")
println(eq4, ",  # eq4")
println(eq5, ",  # eq5")
println(eq6, ",  # eq6")
println(eq7, ",  # eq7")
println(eq8, ",  # eq8")
println(eq9, ",  # eq9")

   x4^2 - (r1 + r4)^2 + (y1 - y4)^2,  # eq1
   -(r2 + r4)^2 + (x3 - x4)^2 + (y3 - y4)^2,  # eq2
   x3^2 - (r1 + r2)^2 + (y1 - y3)^2,  # eq3
   -4*r2^2 + x3^2 + (y2 - y3)^2,  # eq4
   -r1^2 + x^2*y^2*(y - y1)^2/(x^2 + y^2)^2 + (-y*(x^2 + y*y1)/(x^2 + y^2) + y1)^2,  # eq5
   -r4^2 + (-x*(x*x4 + y^2 - y*y4)/(x^2 + y^2) + x4)^2 + (-y*(x^2 - x*x4 + y*y4)/(x^2 + y^2) + y4)^2,  # eq6
   -r2^2 + x^2*y^2*(y + y2)^2/(x^2 + y^2)^2 + (-y*(-x^2 + y*y2)/(x^2 + y^2) + y2)^2,  # eq7
   -r2^2 + (-x*(x*x3 + y^2 + y*y3)/(x^2 + y^2) + x3)^2 + (-y*(-x^2 + x*x3 + y*y3)/(x^2 + y^2) + y3)^2,  # eq8
   -2*y + (1 + sqrt(x^2 + y^2)/x)*(r1 + r2),  # eq9

日円，月円の半径を 5, 4 とする。

using Printf
using Plots

using NLsolve

function nls(func, params...; ini = [0.0])
   if typeof(ini) <: Number
       r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=1e-14)
       v = r.zero[1]
   else
       r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=1e-14)
       v = r.zero
   end
   return v, r.f_converged
end;

function H(u)
   (r1, r2) = (5, 4)
   (r4, y1, y2, x3, y3, x4, y4, y, x) = u
   return [
       x4^2 - (r1 + r4)^2 + (y1 - y4)^2,  # eq1
       -(r2 + r4)^2 + (x3 - x4)^2 + (y3 - y4)^2,  # eq2
       x3^2 - (r1 + r2)^2 + (y1 - y3)^2,  # eq3
       -4*r2^2 + x3^2 + (y2 - y3)^2,  # eq4
       -r1^2 + x^2*y^2*(y - y1)^2/(x^2 + y^2)^2 + (-y*(x^2 + y*y1)/(x^2 + y^2) + y1)^2,  # eq5
       -r4^2 + (-x*(x*x4 + y^2 - y*y4)/(x^2 + y^2) + x4)^2 + (-y*(x^2 - x*x4 + y*y4)/(x^2 + y^2) + y4)^2,  # eq6
       -r2^2 + x^2*y^2*(y + y2)^2/(x^2 + y^2)^2 + (-y*(-x^2 + y*y2)/(x^2 + y^2) + y2)^2,  # eq7
       -r2^2 + (-x*(x*x3 + y^2 + y*y3)/(x^2 + y^2) + x3)^2 + (-y*(-x^2 + x*x3 + y*y3)/(x^2 + y^2) + y3)^2,  # eq8
       -2*y + (1 + sqrt(x^2 + y^2)/x)*(r1 + r2),  # eq9
   ]
end;

iniv = [big"1.0", 1.9, -3.1, 3.1, -1.3, 4, 1.9, 5.4, 9.3]
res = nls(H, ini=iniv);
println(res[2] ? "収束した" : "収束していない")

   収束した

names = ["r4", "y1", "y2", "x3", "y3", "x4", "y4", "y ", "x "]
for i in 1:length(names)
   println("$(names[i]) = $(Float64(res[1][i]))")
end

   r4 = 1.7470608602667996
   y1 = 3.9418436943485617
   y2 = -5.058156305651438
   x3 = 7.166451331820933
   y3 = -1.5026007500958825
   x4 = 6.740960675000237
   y4 = 4.228687607033678
   y  = 9.523406750862943
   x  = 19.195039966835868

星円の半径は 1.7470608602667996。

using Plots
using Printf

function draw(more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r4, y1, y2, x3, y3, x4, y4, y, x) = res[1]
   (r1, r2) = (5, 4)
   r3 = r2
   # y = 5/2 + 5*sqrt(3)/3
   # x = sqrt(3) * y
   @printf("r1 = %.5f;  r2 = %.5f;  \nr4 = %.5f;  y1 = %.5f;  y2 = %.5f;  \nx3 = %.5f;  y3 = %.5f;  x4 = %.5f;  \ny4 = %.5f;  y = %.5f;  x = %.5f\n", r1, r2, r4, y1, y2, x3, y3, x4, y4, y, x)
   plot([x, 0, -x, 0, x], [0, y, 0, -y, 0], color=:black, lw=0.5)
   circle(0, y1, r1)
   circle(0, y2, r2, :blue)
   circle(x3, y3, r3, :blue)
   circle(-x3, y3, r3, :blue)
   circle(x4, y4, r4, :green)
   circle(-x4, y4, r4, :green)
   if more == true
       point(0, y1, " y1\n 日円", :red, :left, :bottom)
       point(0, y2, " y2\n 月円", :blue, :left, :bottom)
       point(x3, y3, "(x3,y3)\n月円", :blue, :left, :center)
       point(x4, y4, "(x4,y4)\n星円", :green, :left, :center)
       point(0, y, " y", :black, :left, :bottom)
       point(x, 0, "x", :black)
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
   else
       plot!(showaxis=false)
   end
end;

算額（その246）

算額（その246）

中村信弥「改訂増補 長野県の算額」
http://www.wasan.jp/zoho/zoho.html
県内の算額3（229)
長野県諏訪市下諏訪 諏訪大社下社 慶応4年(1868)

部分円の中に，大円，小円が 2 個ずつ入っている。大円の径が 147 寸，元の長さが 294 寸のとき，小円の径を求めよ。

弦を x 軸上に取り，その中点を原点とする。弦の右端の x 座標を (x, 0) とする。x = 294/2 である。
部分円の半径を R 中心座標を (0, y) とする。
右の大円の半径，中心座標を r2, (r2, r2)　とする。r2 = 147/2 である。
右の小円の半径，中心座標を r1, (x1, r1) とする。

以下の連立方程式を解く。

include("julia-source.txt");

using SymPy

@syms x::positive, y::positive, r1::positive, x1::positive, r2::positive, R::positive;

x = 294 // 2
r2 = 147 // 2
eq1 = x^2 + y^2 - R^2
eq2 = r2^2 + (r2 - y)^2 - (R - r2)^2
eq3 = x1^2 + (y - r1)^2 - (R - r1)^2
eq4 = (x1 - r2)^2 + (r2 - r1)^2 - (r1 + r2)^2;

res = solve([eq1, eq2, eq3, eq4], (r1, x1, R, y))

   1-element Vector{NTuple{4, Sym}}:
    (27/2, 273/2, 1225/8, 343/8)

r1 = 13.50000;  x1 = 136.50000;  R = 153.12500;  y = 42.87500
小円の半径は 13.5。元の単位で直径は 27 寸である。

eq1 ~ eq4 を x, r2 も未知数（変数）として解くと，r1 は以下の式で求めることができる。

x = 294 // 2
r2 = 147 // 2
num = r2 * (x - r2)^2 * (x + r2)^2
den = (3r2^2 + x^2)^2
r1 = num / den
println(r1)

   27//2

using Plots
using Printf

function draw(more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   # (r1, x1, R, y) = res[1]
   (r1, x1, R, y) = (27/2, 273/2, 1225/8, 343/8)
   x = 294 // 2
   r2 = 147 // 2
  @printf("r1 = %.5f;  x1 = %.5f;  R = %.5f;  y = %.5f\n", r1, x1, R, y)
   θ = atan(y/x)/pi*180
   plot()
   circle(0, y, R, :blue, beginangle=-θ, endangle=180+θ, n=200)
   circle(x1, r1, r1)
   circle(-x1, r1, r1)
   circle(r2, r2, r2, :green)
   circle(-r2, r2, r2, :green)
   segment(x, 0, -x, 0, :blue)
   if more == true
       point(0, y, " y", :blue)
       point(x1, r1, "小円      \n(x1,r1)   ", :red, :right, :bottom)
       point(r2, r2, " 大円\n (r2,r2)", :green, :left, :bottom)
       point(x, 0, "x", :blue)
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5, ylims=(-12, 200))
   else
       plot!(showaxis=false)
   end
end;

算額（その245）

算額（その245）

中村信弥「改訂増補 長野県の算額」
http://www.wasan.jp/zoho/zoho.html
県内の算額3（228)
長野県諏訪市下諏訪 諏訪大社下社 慶応4年(1868)

長方形内に大円 1 個，小円 2個が長方形に接して入っている。長方形の長辺と短辺はそれぞれ 15寸，8寸である。大円と片方の小円の共通接線（界斜）があるとき界斜の長さはいかほどか。

長方形の左下角を原点とする。
大円の半径，中心座標を r2, (r2, r2)　とする。r2 = 4 である。
小円の半径，中心座標を r1, (15 - r1, r1), (15 - r1, 8 - r1) とする。r1 = 2 である。
界斜と長方形の下辺，上辺の交点座標を (x1, 0), (x2, 8) とする。

大円と下側の小円の中心から界斜までの距離に関する以下の連立方程式を解く。

include("julia-source.txt");

using SymPy

@syms r1::positive, r2::positive, x1::positive, x2::positive;

r1 = 2
r2 = 4
eq1 = distance(x1, 0, x2, 8, 15 - r1, r1) - r1^2;
eq2 = distance(x1, 0, x2, 8, r2, r2) - r2^2;

res = solve([eq1, eq2], (x1, x2))

   3-element Vector{Tuple{Sym, Sym}}:
    (5, 20)
    (12, 6)
    (22, 44/9)

二番目の解が適切である。すなわち，界斜は座標 (12, 0), (6, 8) を結ぶ線分。
長さは sqrt((12 - 6)^2 + (8 - 0)^2) = 10 寸である。

sqrt((12 - 6)^2 + (8 - 0)^2)

   10.0

using Plots
using Printf

function draw(more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (x1, x2) = res[2]
   @printf("x1 = %.2f;  x2 = %.2f;  界斜の長さ = %.2f\n", x1, x2, sqrt((x2 - x1)^2 + 8^2))
   plot([0, 15, 15, 0, 0], [0, 0, 8, 8, 0], color=:black, lw=0.5)
   circle(15 - r1, r1, r1)
   circle(15 - r1, 8 - r1, r1)
   circle(r2, r2, r2, :green)
   segment(x1, 0, x2, 8, :blue)
   if more == true
       point(15 - r1, 1.2r1, "小円", :red, :center, :bottom, mark=false)
       point(15 - r1, r1, "\n(15-r1,r1)", :red, :center, :top)
       point(15 - r1, 8 - r1, "\n(15-r1,8-r1)", :red, :center, :top)
       point(r2, 1.1r2, "大円", :green, :center, :bottom, mark=false)
       point(r2, r2, "\n(r2,r2)", :green, :center, :top)
       point(x1, 0, "x1  ", :blue, :right, :bottom)
       point(x2, 8, "  x2", :blue, :left, :top)
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
   else
       plot!(showaxis=false)
   end
end;

算額（その244）

算額（その244）

中村信弥「改訂増補 長野県の算額」
http://www.wasan.jp/zoho/zoho.html
県内の算額3（228)
長野県諏訪市下諏訪 諏訪大社下社 慶応4年(1868)

外円の中に大円，小円が 4 個ずつと正方形が入っている。大円の径を知って小円の径を求めよ。

外円の半径，中心座標を R, (0, 0)
大円の半径，中心座標を r2, (x2, x2)
右側の小円の半径，中心座標を r1, (r1, 0)

以下の連立方程式を解く。R は任意なので，R を含む式で求まる。

include("julia-source.txt");

using SymPy

@syms R::positive, r1::positive, r2::positive, x2::positive;

eq1 = (R - r1 - x2)^2 + x2^2 - (r1 + r2)^2
eq2 = 2x2^2 - (R - r2)^2
eq3 = 4(R - 2r2)^2 - 2(R - 2r1)^2 |> expand;

res = solve([eq1, eq2, eq3], (r1, r2, x2))

   2-element Vector{Tuple{Sym, Sym, Sym}}:
    (R*(-13 - sqrt(467 - 326*sqrt(2)) + 11*sqrt(2))/4, R*(-18 + sqrt(934 - 652*sqrt(2)) + 15*sqrt(2))/8, R*(-15/8 - sqrt(467/64 - 163*sqrt(2)/32) + 13*sqrt(2)/8))
    (R*(-3*sqrt(2) + sqrt(19 - 10*sqrt(2)) + 3)/4, R*(-2 + sqrt(2) + sqrt(38 - 20*sqrt(2)))/8, R*(-sqrt(19 - 10*sqrt(2))/8 - 1/8 + 5*sqrt(2)/8))

二番目の解が適切である。

(R*(-13 - sqrt(467 - 326*sqrt(2)) + 11*sqrt(2))/4,
R*(-18 + sqrt(934 - 652*sqrt(2)) + 15*sqrt(2))/8,
R*(-15/8 - sqrt(467/64 - 163*sqrt(2)/32) + 13*sqrt(2)/8)) |> println

(R*(-3*sqrt(2) + sqrt(19 - 10*sqrt(2)) + 3)/4,
R*(-2 + sqrt(2) + sqrt(38 - 20*sqrt(2)))/8,
R*(-sqrt(19 - 10*sqrt(2))/8 - 1/8 + 5*sqrt(2)/8)) |>  println

   (0.0284330026344626*R, 0.833448221620951*R, 0.117769891910505*R)
   (0.240353914715992*R, 0.316402492387137*R, 0.483376433235278*R)

大円の径を知って小円の径を求めるには，比「小円の径 / 大円の径」が分かればよい。

f = res[2][1] / res[2][2] |> expand |> simplify
f |> println

   2*(-3*sqrt(2) + sqrt(19 - 10*sqrt(2)) + 3)/(-2 + sqrt(2) + sqrt(2)*sqrt(19 - 10*sqrt(2)))

f |> N

   0.7596460852840080105563473006875416586766810646113255778335329777680921720071803

式が複雑なので，f の分母を有理化する。

@syms dummy
f2 = apart(f, dummy)
f2 |> println

   -sqrt(19 - 10*sqrt(2))/4 + 1/4 + 3*sqrt(2)/4

有理化後の式 f2 が元の式 f と等しいことを確認する。

f - f2 |> expand |> simplify

   0

大円の径が分かれば，0.759646 倍すれば，小円の径になる。

   0.949207 * 0.759646 ≒ 0.721062

using Plots
using Printf

function draw(R, more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r1, r2, x2) =  (R*(-3*sqrt(2) + sqrt(19 - 10*sqrt(2)) + 3)/4, R*(-2 + sqrt(2) + sqrt(38 - 20*sqrt(2)))/8, R*(-sqrt(19 - 10*sqrt(2))/8 - 1/8 + 5*sqrt(2)/8))
   @printf("r1 = %.6f;  r2 = %.6f;  x2 = %.6f;  r1/r2 = %.6f\n", r1, r2, x2, r1/r2)
   #@printf("x1 = %.5f;  y1 = %.5f\n", x1, y1)
   plot([R - 2r1, 0, 2r1 - R, 0, R - 2r1], [0, R - 2r1, 0, 2r1 - R, 0], color=:black, lw=0.5)
   circle(0, 0, R)
   circle(R - r1, 0, r1, :green)
   circle(r1 - R, 0, r1, :green)
   circle(0, R - r1, r1, :green)
   circle(0, r1 - R, r1, :green)
   circle4(x2, x2, r2, :blue)
   if more == true
       point(0, R - 0.9r1, " 小円", :green, :left, :bottom, mark=false)
       point(0, R - r1, " R-r1")
       point(R - r1, 0.1r1, " 小円", :green, :left, :bottom, mark=false)
       point(R - r1, 0, " R-r1")
       point(x2, x2 + 0.1r2, " 大円", :blue, :left, :bottom, mark=false)
       point(x2, x2, " (x2,x2)", :blue)
       point(R, 0, " R")
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
   else
       plot!(showaxis=false)
   end
end;

 

分母が複雑な場合の有理化

今まで

f = 2*(-3*sqrt(2) + sqrt(19 - 10*sqrt(2)) + 3)/(-2 + sqrt(2) + sqrt(2)*sqrt(19 - 10*sqrt(2)))

のような，分母に平方根が含まれている式を有理化するとき，二段階に分けて行っていた。一段階での結果を見て第二段階へ行かなくてはならないし，面倒この上ない。

den = denominator(f)
terms = den.args;
temp = -terms[1] - terms[2] + terms[3];

den * temp |> expand;
temp2 = 32 + 16sqrt(Sym(2));
den = den * temp * temp2 |> expand |> simplify;
num = numerator(f) * temp * temp2 |> expand |> simplify;
f2 = num / den
f2 |> println

 

-sqrt(19 - 10*sqrt(2))/4 + 1/4 + 3*sqrt(2)/4

有理化後の式 f2 が元の式 f と等しいことを確認する。

f == f2

trueChatGPT に聞いてみて，驚いた。

apart() があるのは知っていたが，以下のように一発で答えが出るというのは知らなかった。便利だ。

@syms dummy  # 変数は使わないので，何でもよい

apart(f, dummy) |> println

-sqrt(19 - 10*sqrt(2))/4 + 1/4 + 3*sqrt(2)/4

 

算額（その243）

算額（その243）

中村信弥「改訂増補 長野県の算額」
http://www.wasan.jp/zoho/zoho.html
県内の算額3（227)
長野県諏訪市下諏訪 諏訪大社下社 慶応4年(1868)

正三角形とそれに内接する円 2 本の（左右対称な）斜線に接する貞円 3 個，元円，亨円，利円が 1 個ずつある。貞円の径を知って亨円の径を求めよ。

正三角形の一辺の長さを 1 とする。
右側の貞円の半径，中心座標を r1, (x1, y1)
下側の貞円の半径，中心座標を r1, (-r1, 0)
内接円の半径，中心座標を r2, (0, r2)
元円の半径，中心座標を r3, (0, r3)
利円の半径，中心座標を r4, (0, -2r1-r4)
亨円の半径，中心座標を r5, (0, -2r1-2r4-r5)
とする。
2 本の斜線の狭角の 1/2 を θとすると，sinθ= (√3 - r2) / (r2 - 2r1) である。
また，r2 = 1/√3，x1 = (r1 + r2)cos(π/6), y1 = (r1 + r2)sin(π/6) + r2 である。
以下の連立方程式を解く。

include("julia-source.txt");

using SymPy

@syms r1::positive, x1::positive, y1::positive, r2::positive, r3::positive, r4::positive, r5::positive;

r2 = 1/√Sym(3)
sinθ = (r2 - 2r1) / (√Sym(3) - r2)
cosθ = sqrt(1 - sinθ^2);

sqrt3 = sqrt(Sym(3))
eq1 = (sqrt3 + r1)sinθ - r1 |> expand
eq2 = (sqrt3 - r3)sinθ - r3 |> expand
eq3 = (sqrt3 + 2r1 + r4)sinθ - r4 |> expand
eq4 = (sqrt3 + 2r1 + 2r4 + r5)sinθ - r5 |> expand;

(r1, r3, r4, r5) = solve([eq1, eq2, eq3, eq4], (r1, r3, r4, r5))[1]

   (-7*sqrt(3)/12 + sqrt(219)/12, -sqrt(219)/24 + 11*sqrt(3)/24, -sqrt(219)/9 + 10*sqrt(3)/9, -83*sqrt(3)/54 + 11*sqrt(219)/54)

   r1 = 0.22286;  r2 = 0.57735;  r3 = 0.17725;  r4 = 0.28021; r5 = 0.35231
   x1 = 0.35218;  y1 = 0.61776

亨円と貞円の半径（直径）の比を求める。

(r5 / r1) |> simplify |> println

   37/18 - sqrt(73)/18

術では「74 から 292 の平方根を引き，貞円の径を掛け，36 で割れば亨円の径を得る」と言っている。分子分母を2倍しているだけで，同じである。

(74 - sqrt(Sym(292)))/36 |> simplify |> println

   37/18 - sqrt(73)/18

新しい術「37 から 73 の平方根を引き，貞円の径を掛け，18 で割れば亨円の径を得る」

(r5 / r1) * 0.22286 |> N

   0.352316851406585282011764975423176304679348938046109770889125810268254317780704

ついでに，利円，元円，内接円の半径（直径）と貞円の半径（直径）の関係を求めておく。

r4 / r1 |> simplify |> println  # 利円

   -1/6 + sqrt(73)/6

r3 / r1 |> simplify |> println  # 元円

   1/12 + sqrt(73)/12

r2 / r1 |> simplify |> println  # 内接円

   7/6 + sqrt(73)/6

using Plots
using Printf
function draw(more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   sqrt3 = sqrt(3)
   r2 = 1/sqrt3
   (x1, r1, r3, r4, r5) = (5/24 + sqrt(2)*sqrt(61 - 7*sqrt(73))/6 + sqrt(73)/24, -7*sqrt(3)/12 + sqrt(219)/12, -sqrt(219)/24 + 11*sqrt(3)/24, -sqrt(219)/9 + 10*sqrt(3)/9, -83*sqrt(3)/54 + 11*sqrt(219)/54)
   sinθ = (r2 - 2r1) / (sqrt3 - r2)
   cosθ = sqrt(1 - sinθ^2)
   tanθ = sinθ / cosθ
   x1 = (r2 - r1)cosθ
   y1 = (r2 - r1)sinθ + r2
   @printf("r1 = %.5f;  r2 = %.5f;  r3 = %.5f;  r4 = %.5f; r5 = %.5f\n", r1, r2, r3, r4, r5)
   @printf("x1 = %.5f;  y1 = %.5f\n", x1, y1)
   plot([1, 0, -1, 1], [0, sqrt3, 0, 0], color=:black, lw=0.5)
   circle(0, r2, r2)
   circle(0, r3, r3, :green)
   circle(0, -r1, r1, :blue)
   circle(x1, y1, r1, :blue)
   circle(-x1, y1, r1, :blue)
   circle(0, -2r1-r4, r4, :brown)
   circle(0, -2r1-2r4-r5, r5, :gold)
   segment(0, sqrt3, 3.5tanθ, sqrt3 - 3.5)
   segment(0, sqrt3, -3.5tanθ, sqrt3 - 3.5)
   if more == true
       point(0, 1/sqrt3, "1/√3 ", :red, :right)
       point(x1, y1, "(x1,y1)")
       point(x1, y1, " 貞円", :blue, :left, :bottom, mark=false)
       point(1, 0, " 1")
       point(0, sqrt3, " √3")
       point(0, r3, " r3")
       point(0, r3, " 元円", :green, :left, :bottom, mark=false)
       point(0, -r1, " -r1")
       point(0, -r1, " 貞円", :blue, :left, :bottom, mark=false)
       point(0, -2r1-r4, " -2r1-r4", :brown)
       point(0, -2r1-r4, " 利円", :brown, :left, :bottom, mark=false)
       point(0, -2r1-2r4-r5, " -2r1-2r4-r5", :gold)
       point(0, -2r1-2r4-r5, " 亨円", :gold, :left, :bottom, mark=false)
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
   else
       plot!(showaxis=false)
   end
end;

算額（その242）

算額（その242）

中村信弥「改訂増補 長野県の算額」
http://www.wasan.jp/zoho/zoho.html
県内の算額3（206)
長野県長野市芋井笹峯 笹峯天神社 文久2年(1862)

鉤股弦の中に大円と小円が入っている。長弦 3寸2分，短弦 1寸8分，中鉤 2寸4分のとき大円，小円の径を求めよ。

鉤股弦（直角三角形）の長弦とは AD，短弦とは CD，中鉤とは BD をいう。
鉤股弦に内接する円の直径は「鉤 + 股 - 弦」である。
AD = x, BC = y とおく。
小円の半径，中心座標を r1, (x - r1, y1)
大円の半径，中心座標を r2, (x2, r2)

x, y, r1, r2, y1, x2 の順に求める。

include("julia-source.txt");

using SymPy

@syms x::positive, y::positive, r1::positive, r2::positive, y1::positive, x2::positive;

eq1 = x^2 - (3.2^2 + 2.4^2)  # AB = x
x = solve(eq1)[1];

eq2 = y^2 - (1.8^2 + 2.4^2)  # BC = y
y = solve(eq2)[1];

eq3 = 2r1 -(1.8 + 2.4 - 3.0)
r1 = solve(eq3)[1];

eq4 = 2r2 - (2.4 + 3.2 - 4.0)
r2 = solve(eq4)[1];

eq5 = y1 + r1 - 2.4
y1 = solve(eq5)[1];

eq6 = x2 + r2 - 3.2
x2 = solve(eq6)[1];

x, y, r1, y1, r2, x2

   (4.00000000000000, 3.00000000000000, 0.600000000000000, 1.80000000000000, 0.800000000000000, 2.40000000000000)

小円，大円の半径がそれぞれ 6分，8分なので，直径は 1寸2分，1寸6分である。

using Plots
using Printf

function draw(more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (x, y, r1, y1, r2, x2) = (4.0, 3.0, 0.6, 1.8, 0.8, 2.4)
   @printf("x = %.3f;  y = %.3f;  r1 = %.3f;  y1 = %.3f;  r2 = %.3f;  x2 = %.3f\n", x, y, r1, y1, r2, x2)
   plot([0, x, x, 0], [0, 0, y, 0], color=:black, lw=0.5)
   circle(x - r1, y1, r1)
   circle(x2, r2, r2, :blue)
   (x0, y0) = 3.2 .* (4//5, 3//5)
   segment(x, 0, x0, y0)
   if more == true
       point(0, 0, "A ", :black, :right, :bottom)
       point(x, 0, " B", :black, :left, :bottom)
       point(x, y, " C" , :black, :left, :bottom)
       point(x0, y0, "D ", :black, :right, :bottom)
       point(4.0 - r1, y1, "(4-r1,y1)", :red, :center, :top)
       point(4.0 - r1, 1.1y1, " 小円", :red, :left, :bottom, mark=false)
       point(x2, r2, "(x2,r2)", :blue, :center, :top)
       point(x2, 1.1r2, " 大円", :blue, :left, :bottom, mark=false)
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5, xlims=(-0.2, 4.2))
   else
       plot!(showaxis=false)
   end
end;

算額（その241）

算額（その241）

中村信弥「改訂増補 長野県の算額」
http://www.wasan.jp/zoho/zoho.html
県内の算額3（227)
長野県諏訪市下諏訪 諏訪大社下社 慶応4年(1868)

2 個の大円が交わり，その中に長方形と小円が 4 個入っている。小円の径を知って，大円の径を求めよ。

大円に接する長方形の右上の頂点座標を (x, y) とおく。
大円，小円の半径と中心座標を以下のようにおく。

大円: r1, (x1, 0)　ただし与えられた条件より r1 = 1 とする。
小円: r2, (0, y + r2) および (x + r2, 0)

以下の連立方程式を立てるが，問では条件が一つ足りない。そこで，x と y の間に x = ny のような制約条件を追加して解く（以下では x = 2y とした）。

なお，nlsolve() ではこの制約条件を追加しなくても一応の解は得られる。

include("julia-source.txt");

using SymPy

@syms x::positive, y::positive, r1::positive, x1::positive, r2::positive;

r2 = 1
x = 2y
eq1 = (x - x1)^2 + y^2 - r1^2 |> expand
eq2 = x - x1 + 2r2 - r1 |> expand
eq3 = x1^2 + (y + r2)^2 - (r1 - r2)^2 |> expand
eq4 = ((2r1 - 2r2)^2 + y^2) + (4r2^2 + y^2) - (2r1)^2 |> expand;

res = solve([eq1, eq2, eq3], (x1, r1, y))

   1-element Vector{Tuple{Sym, Sym, Sym}}:
    (-5*sqrt(2)*(8*sqrt(2) + 71)^(2/3)/289 + sqrt(2)*(8*sqrt(2) + 71)^(1/3)/34 + 21/16 + 99*(8*sqrt(2) + 71)^(1/3)/272 + 421*(8*sqrt(2) + 71)^(2/3)/4624, -3*sqrt(2)*(8*sqrt(2) + 71)^(2/3)/289 - sqrt(2)*(8*sqrt(2) + 71)^(1/3)/34 + 173*(8*sqrt(2) + 71)^(1/3)/272 + 715*(8*sqrt(2) + 71)^(2/3)/4624 + 59/16, 3/2 + 17/(4*(sqrt(2) + 71/8)^(1/3)) + (sqrt(2) + 71/8)^(1/3))

    x1 = 4.33657; r1 = 8.92148; y = 5.62902; x = 11.25805

小円の半径を 1 としたので，8.92148 は大円の半径である。

using Printf
function draw(x1, r1, x, y, more)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r2 = 1
   @printf("x1 = %.5f; r1 = %.5f; y = %.5f; x = %.5f\n", x1, r1, y, x)
   plot([x, x, -x, -x, x], [-y, y, y, -y, -y], color=:black, lw=0.5)
   circle(x1, 0, r1)
   circle(-x1, 0, r1)
   circle(0, y + r2, r2, :green)
   circle(0, -y - r2, r2, :green)
   circle(x + r2, 0, r2, :green)
   circle(-x - r2, 0, r2, :green)
   if more == true
       point(x1, 0, "x1 ", :red, :right)
       point(x + r2, 0, "x+r2 ", :green, :right)
       point(0, y + r2, "    y+r2", :green, :left, :bottom)
       point(x + 2r2, 0, " x+2r2", :red)
       point(x, y, " (x,y)", :red, :left, :bottom)
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
   else
       plot!(showaxis=false)
   end
end;

(x1, r1, y) = res[1]

---

条件不足のまま 4元連立方程式を nlsolve() で x1, r1, x, y について解く。

using SymPy

@syms x::positive, y::positive, r1::positive, x1::positive, r2::positive;

r2 = 1
eq1 = (x - x1)^2 + y^2 - r1^2 |> expand
eq2 = x - x1 + 2r2 - r1 |> expand
eq3 = x1^2 + (y + r2)^2 - (r1 - r2)^2 |> expand
eq4 = ((2r1 - 2r2)^2 + y^2) + (4r2^2 + y^2) - (2r1)^2 |> expand;

println(eq1, ",  # eq1")
println(eq2, ",  # eq2")
println(eq3, ",  # eq3")
println(eq4, ",  # eq4")

   -r1^2 + x^2 - 2*x*x1 + x1^2 + y^2,  # eq1
   -r1 + x - x1 + 2,  # eq2
   -r1^2 + 2*r1 + x1^2 + y^2 + 2*y,  # eq3
   -8*r1 + 2*y^2 + 8,  # eq4

using NLsolve

function nls(func, params...; ini = [0.0])
   if typeof(ini) <: Number
       r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=1e-14)
       v = r.zero[1]
   else
       r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=1e-14)
       v = r.zero
   end
   return v, r.f_converged
end;

function H(u)
   r1 = 1
   (x1, r1, x, y) = u
   return [
       -r1^2 + x^2 - 2*x*x1 + x1^2 + y^2,  # eq1
       -r1 + x - x1 + 2,  # eq2
       -r1^2 + 2*r1 + x1^2 + y^2 + 2*y,  # eq3
       -8*r1 + 2*y^2 + 8,  # eq4
      ]
end;

iniv = [big"4.0", 9, 10, 6]
res2 = nls(H, ini=iniv);
println((res2));

   (BigFloat[3.183012652585522591832434702426538376856770104448615704443237602882606475256619, 8.076648273506633325075325119429150245928992397056981109398659352229911092241916, 9.259660926092155916907759821855688622785762501505596813841896955962457886997144, 5.320394073189178089410508073953356392935683449161830208448592642794610637849292], true)

   x1 = 3.18301; r1 = 8.07665; y = 5.32039; x = 9.25966

算額（その240）

算額（その240）

中村信弥「改訂増補 長野県の算額」
http://www.wasan.jp/zoho/zoho.html
県内の算額3（226)
長野県諏訪市下諏訪 諏訪大社下社 慶応4年(1868)

外円の中に天円 4 個，地円 6 個，人円 4 個が入っている。天円の径が与えられたとき，人円の径を求めよ。

外円，天円，地円，人円の半径と中心座標を以下のようにおく。

外円: R, (0, 0)
天円: r1, (x1, r1)
地円: r2, (0, 0) および (x2, r2)
人円: r3, (x3, y3)

天円の半径が与えれれるので，r1 = 1 とおく。
また，x2 = 2x1 である。
注: 天円は，y 軸とは接していない。

include("julia-source.txt");

以下の 3 本の方程式は，x1, r2, R についてのもので，solve() で解を求めることができる。

using SymPy

@syms r1::positive, x1::positive, r2::positive, x2::positive, r3::positive, x3::positive, y3::positive, R::positive;

r1 = 1
x2 = 2x1
eq1 = x1^2 + r1^2 - (R - r1)^2
eq2 = x2^2 + r2^2 - (R - r2)^2
eq3 = (x2 - x1)^2 + (r1 - r2)^2 - (r1 + r2)^2;

solve([eq1, eq2, eq3], (x1, r2, R))

   1-element Vector{Tuple{Sym, Sym, Sym}}:
    (sqrt(28 - 12*sqrt(5)), 7 - 3*sqrt(5), -2 + 2*sqrt(5))

しかし，x1, r2, R が決まったあと，r3, x3, y3 を求めるための残りの 3 本の方程式は solve() で解くことができない。

eq4 = x3^2 + y3^2 - (R - r3)^2
eq5 = (x3 - x1)^2 + (r1 - y3)^2 - (r1 + r3)^2
eq6 = (x3 - x2)^2 + (y3 - r2)^2 - (r3 + r2)^2;

それで，結局のところ 6 本の連立方程式を nlsolve() で解くことにする。

println(eq1, ",  # eq1")
println(eq2, ",  # eq2")
println(eq3, ",  # eq3")
println(eq4, ",  # eq4")
println(eq5, ",  # eq5")
println(eq6, ",  # eq6")

   x1^2 - (R - 1)^2 + 1,  # eq1
   r2^2 + 4*x1^2 - (R - r2)^2,  # eq2
   x1^2 + (1 - r2)^2 - (r2 + 1)^2,  # eq3
   x3^2 + y3^2 - (R - r3)^2,  # eq4
   (1 - y3)^2 - (r3 + 1)^2 + (-x1 + x3)^2,  # eq5
   (-r2 + y3)^2 - (r2 + r3)^2 + (-2*x1 + x3)^2,  # eq6

using NLsolve

function nls(func, params...; ini = [0.0])
   if typeof(ini) <: Number
       r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=1e-14)
       v = r.zero[1]
   else
       r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=1e-14)
       v = r.zero
   end
   return v, r.f_converged
end;

function H(u)
   r1 = 1
   (x1, r2, r3, x3, y3, R) = u
   # println(u)
   return [
x1^2 - (R - 1)^2 + 1,  # eq1
r2^2 + 4*x1^2 - (R - r2)^2,  # eq2
x1^2 + (1 - r2)^2 - (r2 + 1)^2,  # eq3
x3^2 + y3^2 - (R - r3)^2,  # eq4
(1 - y3)^2 - (r3 + 1)^2 + (-x1 + x3)^2,  # eq5
(-r2 + y3)^2 - (r2 + r3)^2 + (-2*x1 + x3)^2,  # eq6
      ]
end;

iniv = [big"1.1", 0.3, 0.14, 2.25, 0.75, 2.5]
res = nls(H, ini=iniv);
println(res);

   (BigFloat[1.080363026950906962773783583238333577245845592041721754016512840267774995583403, 0.2917960675006310117247564105634979118556556424332539734005336141870321167000515, 0.1519553880558686263724085395974730657224106667858737670157781675475329832318468, 2.201116552320873166994524966387851524880342069547970579400755429309693477168625, 0.7337055174402905594576728270074182849955867099200287269565993335856897130533752, 2.472135954999580224200317035334459839068561852275454446131625344134375443426156], true)

   x1 = 1.08036;  r2 = 0.29180;  r3 = 0.15196;  x3 = 2.20112;  y3 = 0.73371;  R = 2.47214

人円の半径は「天円の径 × 0.15196」である。

using Printf
function draw(more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (x1, r2, r3, x3, y3, R) = res[1]
   @printf("x1 = %.5f; r2 = %.5f; r3 = %.5f; x3 = %.5f; y3 = %.5f; R = %.5f\n", x1, r2, r3, x3, y3, R)
   r1 = 1
   x2 = 2x1
   plot()
   circle(0, 0, R)
   circle4(x1, r1, r1, :brown)
   circle(0, r2, r2, :green)
   circle(0, -r2, r2, :green)
   circle4(x2, r2, r2, :green)
   circle4(x3, y3, r3, :blue)
   if more == true
       point(x1, r1, "(x1,r1)", :brown)
       point(0, r2, " r2")
       point(x2, r2, "(x2,r2)", :green, :right)
       point(x3, y3, "(x3,y3)  ", :blue, :right)
       point(0, R, " R", :red)
       point(1.2x1, 1.2r1, "天円", :brown, mark=false)
       point(0.3r2, 1.7r2, "地円", :green, mark=false)
       point(x2+0.3r2, 1.7r2, "地円", :green, mark=false)
       point(x3+0.3r3, y3+1.7r3, "人円", :blue, mark=false)
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
   else
       plot!(showaxis=false)
   end
end;