隣の人と異なる仮装
締め切りが 2017/10/31 10:00 AM なので,その 1 分後に投稿されるように予約
いよいよハロウィンの季節がやってきました。
ハロウィンと言えば仮装ですね。
ただ、せっかく仮装しても他の人と同じ衣装になるのは避けたいもの。
そこで、全員が横一列に並んだときに、隣の人とは異なる仮装をすることにしました。
m 人が仮装をしたとき、衣装の数がちょうど n 種類である「並び方」が何通りあるかを求めてください。
例えば、m = 5, n = 3 のとき、同じ文字が同じ衣装を表すものとすると、以下の7通りの並び方があります。
(1) A B A B C
(2) A B A C A
(3) A B A C B
(4) A B C A B
(5) A B C A C
(6) A B C B A
(7) A B C B C
※衣装の内容は問わないものとし、衣装を入れ替えたものは同じと考えます。
(例:B A B A Cは(1)と同じなのでカウントしない。)
標準入力から m, n が与えられたとき、その並び方が何通りあるかを求め、標準出力に出力してください。
なお、m, n はともに整数で 0 < n < m < 20 を満たすものとします。
【入出力サンプル】
標準入力
5 3
標準出力
7
===============================================================
これは,第2種スターリング数 f(m-1, n-1)
f = function(n, k) {
# The Stirling numbers of the second kind S(n, k)
ans = 0
for (j in 0:k) {
ans = ans+(-1)^(k-j)*choose(k, j)*j^n
}
cat(ans/factorial(k))
}
第2種スターリング数であることは,以下のプログラムで求める m, n の小さいときの結果を考察してのこと。
bincombinations = function (p) {
retval = matrix(0, nrow = 2^p, ncol = p)
for (n in 1:p) {
retval[, n] = rep(c(rep(0, (2^p/2^n)), rep(1, (2^p/2^n))),
length = 2^p)
}
retval
}
tricombinations = function(p) {
retval = matrix(0, nrow = 3^p, ncol = p)
for (n in 1:p) {
retval[, n] = rep(c(rep(0, (3^p/3^n)), rep(1, (3^p/3^n)), rep(2, (3^p/3^n))),
length = 3^p)
}
retval
}
quatrcombinations = function(p) {
retval = matrix(0, nrow = 4^p, ncol = p)
for (n in 1:p) {
retval[, n] = rep(c(rep(0, (4^p/4^n)), rep(1, (4^p/4^n)), rep(2, (4^p/4^n)), rep(3, (4^p/4^n))),
length = 4^p)
}
retval
}
quintcombinations = function(p) {
retval = matrix(0, nrow = 5^p, ncol = p)
for (n in 1:p) {
retval[, n] = rep(c(rep(0, (5^p/5^n)), rep(1, (5^p/5^n)), rep(2, (5^p/5^n)), rep(3, (5^p/5^n)), rep(4, (5^p/5^n))),
length = 5^p)
}
retval
}
sextetcombinations = function(p) {
retval = matrix(0, nrow = 6^p, ncol = p)
for (n in 1:p) {
retval[, n] = rep(c(rep(0, (6^p/6^n)), rep(1, (6^p/6^n)), rep(2, (6^p/6^n)), rep(3, (6^p/6^n)), rep(4, (6^p/6^n)), rep(5, (6^p/6^n))),
length = 6^p)
}
retval
}
septetcombinations = function(p) {
retval = matrix(0, nrow = 7^p, ncol = p)
for (n in 1:p) {
retval[, n] = rep(c(rep(0, (7^p/7^n)), rep(1, (7^p/7^n)), rep(2, (7^p/7^n)), rep(3, (7^p/7^n)), rep(4, (7^p/7^n)), rep(5, (7^p/7^n)), rep(6, (7^p/7^n))),
length = 7^p)
}
retval
}
f = function(m, n) {
if (n == 2) {
a = bincombinations(m-1)
} else if (n == 3) {
a = tricombinations(m-1)
} else if (n == 4) {
a = quatrcombinations(m-1)
} else if (n == 5) {
a = quintcombinations(m-1)
} else if (n == 6) {
a = sextetcombinations(m-1)
} else if (n == 7) {
a = septetcombinations(m-1)
}
a = cbind(0, a[a[,1] != 0,, drop=FALSE])
b = rep(1, nrow(a))
for (i in 1:(m-1)) {
b = b & (a[,i] != a[,i+1])
}
a = a[b,, drop=FALSE]
b = apply(a, 1, function(x) sum(0:(n-1) %in% x) == n)
a = a[b,, drop=FALSE]
nrow(a)/factorial(n-1)
}
カーペット
締め切りが 2017/10/27 10:00 AM なので,その 1 分後に投稿されるように予約
【概要】
上図のように、正の整数が全て並んでいます。
数をひとつ指定しますので、その数に上下左右に隣接しているマスの数を、昇順にコンマ区切りで出力して下さい。
【入出力】
入力は
3
のようになっています。
ふつうに10進数です。
出力は、入力で指定された数に上下左右に隣接しているマスの数を、昇順にコンマ区切りで出力して下さい。
2,4,9
のような感じです。
【例】
入力 出力
3 2,4,9
20 19,21,72
100 99,101,184
【補足】
• 不正な入力に対処する必要はありません。
• 入力は、1以上 100万 以下です。
• Wikipedia - シェルピンスキーのカーペットが参考になるかもしれません(ならないかもしれません)。
=====================================================================
規則性をプログラムできれば簡単。
f = function(n) {
x = 8^(0:6)
size = 1
result = matrix(NA, 2187, 2187)
result[1, 1] = 1
for (k in 1:7) {
a = result[1:size, 1:size]
size0 = 1:size
size1 = size + 1:size
size2 = size * 2 + 1:size
result[size0, size1] = a + x[k]
result[size0, size2] = a + x[k]*2
result[size1, size0] = a + x[k]*7
result[size1, size2] = a + x[k]*3
result[size2, size0] = a + x[k]*6
result[size2, size1] = a + x[k]*5
result[size2, size2] = a + x[k]*4
size = size * 3
}
result = cbind(result, result[,1]+8^7) # 次のレベルの 1 列を付加
index = which(result == n, arr.ind = TRUE)
i = index[1]
j = index[2]
ans = c(result[i-1, j], result[i+1, j], result[i, j-1], result[i, j+1])
cat(sort(ans[!is.na(ans)]), sep = ",")
}
# f(scan(file("stdin", "r")))
f(1) # 2,8
f(2) # 1,3
f(4) # 3,5,16
f(10) # 9,11
f(101) # 100,102,183
f(1011) # 1001,1010,1012,1021
f(10008) # 9996,10001,10007
f(2341) # 2340,2342,7607,29843
f(16385) # 15799,16386,16392,21651
f(18725) # 18724,18726,60855,238739
f(902876) # 902875,902877,4190208
f(1000000) # 999580,999993,999999
「ループ・トラッキング」問題
締め切りが 2017/10/26 10:00 AM なので,その 1 分後に投稿されるように予約
自然数 n に対し、関数 Fn(x) を次のように定義します(floor():床関数)。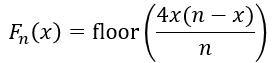
例えば n=10, x=1 のとき、F10(1) = floor(4×1×9÷10) = 3 です。
さて、整数 k(0 ≦ k ≦ n)に対して、関数 Fn による変換を繰り返し行います。
例えば n=10, k=1 のとき、F10 で 1 を変換すると 3 となり、さらに変換すると 8 となります。
以降、1 → 3 → 8 → 6 → 9 → 3 → 8 → … と値が変わっていきます。
このように変換を繰り返したときに、今までに出た値が再度現れるまでの変換回数を G(n, k) と定義します。
例えば G(10, 1)=5 です。5 回目の変換で 3 の値が再度現れていることが分かります(上の太字部分)。
同様に、G(10, 6)=4, G(10, 0)=1, G(10, 5)=3, G(20, 6)=8 となることが確かめられます。
0 以上 n 以下の全ての整数 k に対する G(n, k) の和を H(n) と定義します。
例えば H(10)=42, H(20)=91, H(100)=1118 となることが確かめられます。
標準入力から、自然数 n(1 ≦ n ≦ 3×105)が与えられます。
標準出力に H(n) の値を出力するプログラムを書いてください。
=============================================================================
R で簡素に書くと以下の通り。しかし,実行時間は掛かる。
f = function(n, x) {
floor(4*x*(n-x)/n)
}
g = function(n, k) {
nxt = pool = k
count = 0
repeat {
nxt = f(n, nxt)
count = count+1
if (nxt %in% pool) {
return(count)
}
pool = c(pool, nxt)
}
}
h = function(n) {
sum = 0
for (k in 0:n) {
sum = sum+g(n, k)
}
sum
}
h(35) # 226
h(350) # 8877
h(1908) # 99344
h(61922) # 8504585
h(99999) # 35499513
h(299997) # 204796803
> h(35) # 226
[1] 226
> h(350) # 8877
[1] 8877
> h(1908) # 99344
[1] 99344
Java や C++ で,いくつものこそくな手段を弄して書いても,h(299997) には,手元のパソコンでも 1.5 sec. ほど掛かってしまうのだ。
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
if (false) {
Scanner cin = new Scanner(System.in);
String line;
line = cin.nextLine();
int n = Integer.parseInt(line);
h(n);
} else {
long start = System.currentTimeMillis();
// h(35); // 226
//h(350); // 8877
// h(1908); // 99344
// h(61922); // 8504585
// h(99999); // 35499513
// h(299997); // 204796803
long end = System.currentTimeMillis();
System.out.println((end - start) + "ms");
}
}
static void h(int n) {
boolean[] exists = new boolean[n + 1];
double n4 = 4.0 / n;
int sum = 0;
int[] suf = new int[n + 1];
for (int k = 0; n >= k; k++) {
int next;
next = k;
exists[next] = true;
int c = 0;
suf[c++] = next;
int count = 0;
for (;;) {
next = (int) (n4 * next * (n - next));
count++;
if (exists[next]) {
sum += count;
break;
}
exists[next] = true;
suf[c++] = next;
}
for (int i = 0; i < c; i++) {
exists[suf[i]] = false;
}
}
System.out.println(sum);
}
}
> urinomics
> 出典:『Wiktionary』 (2010/09/03 02:49 UTC 版)
> 語源
> urine + -omics
> 名詞
> urinomics (uncountable)
> (physiology) The identification of the totality of the constituents of the urine of an organism
少し前に言っていた,「コイケノミクス」にしておけばよかったのにね(藁)
せいぜい,かわいこぶって,「ゆりちゃのみくす」って。茶飲みを連想してほのぼのするか?しないなあ。
に,してもだ。「なんとかのみくす」って,いい加減やめにしないか?
おおもとは,レーガノミクスだっけ。
アベノミクスは,アホノミクスとさんざんいじられたのだよ。
正六角形ブロックの回転
締め切りが 2017/10/06 10:00 AM なので,その 1 分後に投稿されるように予約
【概要】
下図のような、正六角形マス目の集まりがあります。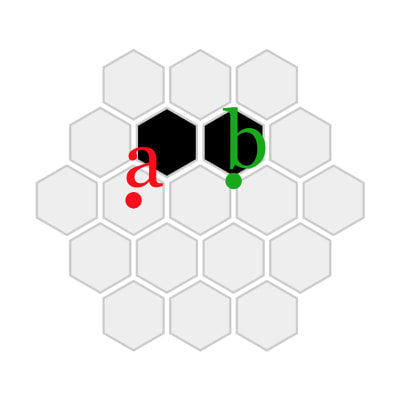
マス目のうちのいくつかにブロックが入っています。
中心を指定するので、そこを中心にブロックを時計回りに 120度回したらどうなるのかを計算して下さい。
【入出力】
入力は
a 000/0110/00000/0000/000
のようになっています。
空白の前は中心を示す記号です。
a, b のいずれかで、図の a点、b点に対応しています。
空白のあとは、マス目の状況を示しています。
スラッシュ区切りで各行の状況を上から順にならべています。
「1」がブロックあり、「0」がブロックなしのマスを示します。
出力は、回転したあとのブロックの状況を
000/0000/00000/0100/100
のような感じで。
入力の時と同様、各行の状況を上から順にスラッシュ区切りでならべて下さい。
ただし、
b 111/0101/00000/0100/111
のように、回転するともとのマス目からはみ出してしまう場合は
-
を出力して下さい。
【例】
入力 出力
a 000/0110/00000/0000/000 000/0000/00000/0100/100


b 111/0101/00000/0100/111 -
b 010/0011/01010/0100/000 011/0000/00111/0010/000

================================================================================
f = function(s) {
type = substr(s, 1, 1) # a か b
s = gsub("/", "", substr(s, 3, 25))
pos = as.integer(unlist(strsplit(s, ""))) # 黒塗りされた正六角形場所左上から右・下へ 1〜19
r3 = sqrt(3)/2
# a を中心としたときの,それぞれの正六角形の中心の座標(x, y)
x = c( 0.0, 1.0, 2.0,
-0.5, 0.5, 1.5, 2.5,
-1.0, 0.0, 1.0, 2.0, 3.0,
-0.5, 0.5, 1.5, 2.5,
0.0, 1.0, 2.0)
y = rep(r3*(2:-2), c(3, 4, 5, 4, 3))
if (type == "b") { b を中心としたときの,それぞれの正六角形の中心の座標(x, y)
x = x-1.5
y = y-sqrt(3)/6
}
n = sum(pos)
x2 = x[pos==1] # 黒塗りされた正六角形の中心の座標(x, y)
y2 = y[pos==1]
xy = cbind(x2, y2)
theta = pi*2/3 # 120度座標軸を回転
rot.xy = xy %*% matrix(c(cos(theta), sin(theta), -sin(theta), cos(theta)), 2)
ans = integer(19)
for (i in seq_len(n)) { # はみ出すかどうかチェック
ok = FALSE
for (j in seq_along(x)) {
if (isTRUE(all.equal(rot.xy[i, 1], x[j])) && isTRUE(all.equal(rot.xy[i, 2], y[j]))) {
ok = TRUE
ans[j] = 1 # はみ出さない正六角形の位置に 1 をセット
break
}
}
if (ok == FALSE) {
break
}
}
if (ok == FALSE) { # はみ出す正六角形があるとき
cat("-")
} else { # 全部内部にあるとき
cat(ans[1:3], "/", ans[4:7], "/", ans[8:12], "/", ans[13:16], "/", ans[17:19], sep="")
}
}
# f(readLines(file("stdin", "r")))
f("a 110/1010/11100/1100/000") # 000/1100/11100/1010/110
f("b 000/0011/01101/0001/010") # 101/0010/01010/0110/000
f("a 000/0100/01100/0000/000") # 000/0000/01000/1100/000
f("b 000/0011/00111/0011/010") # 100/0110/01110/0110/000
f("a 100/0100/10100/0100/000") # 000/0100/10000/1110/000
f("b 000/0100/00110/0000/011") # 100/1011/00100/0000/000
f("a 000/1100/01100/0000/000") # 000/0000/01100/1100/000
f("b 000/0011/00000/0010/010") # 100/0100/00010/0010/000
f("a 010/0111/11000/0000/101") # -
f("b 110/0000/10000/0110/010") # -
f("a 110/1101/01001/1010/000") # -
f("b 011/1111/10000/0110/111") # -
ISBNのチェックディジットを計算して!
締め切りが 2017/10/03 10:00 AM なので,その 1 分後に投稿されるように予約
設問
入力ミスなどを防ぐため、チェックディジットがよく使われます。
代表的な例として、書籍を管理するときに使われるISBN(Wikipedia)があり、チェックディジットが使われています。
ISBNには、かつて使われていた「ISBN-10」と現在主に使われている「ISBN-13」があります。
最近出版されている書籍には両方が記載されていることが一般的で、ISBN-10も使用可能です。
現在、日本国内で出版されたものについては、チェックディジットを除いた部分にISBN-10とISBN-13で同じ値が使われています。
(ISBN-10は「ISBN4-ABCD-EFGH-X」、ISBN-13は「ISBN978-4-ABCD-EFGH-Y」という形で、
ABCD-EFGHの部分は同じ、XとYがそれぞれのチェックディジット)
このABCD-EFGHがすべて異なる数字で構成され、ISBN-10とISBN-13のチェックディジットが同じ(X=Y)ものを調べることにします。
例えば、ABCD-EFGHの部分が「05192743」のものは、ISBN-10では「ISBN4-0519-2743-1」、ISBN-13では「ISBN978-4-0519-2743-1」となり、チェックディジットがともに1となります。
なお、ISBNの計算方法は以下の通りです。(Wikipediaより引用)
ISBN-10
「モジュラス11 ウェイト10-2」という計算法にて算出される。(チェックディジットを除いた左側の桁から10、9、8…2を掛けてそれらの和を取る。和を11で割って出た余りを11から引く)
ここで、例として ISBN4-10-109205-□ のチェックディジット(□部分)を求めてみる。
4×10 + 1×9 + 0×8 + 1×7 + 0×6 + 9×5 + 2×4 + 0×3 + 5×2
= 40 + 9 + 0 + 7 + 0 + 45 + 8 + 0 + 10
= 119
119 ÷ 11 = 10 あまり 9
11 - 9 = 2
よって、このISBNのチェックディジットは2である。なお、計算結果が10になった場合、10の代わりにX(アルファベットの大文字)を用いる。また、11になった場合は、0となる。
ISBN-13
「モジュラス10 ウェイト3・1(モジュラス10 ウェイト3)」という計算法にて算出される。(チェックディジットを除いた一番左側の桁から順に1、3、1、3…を掛けてそれらの和を取る。和を10で割って出た余りを10から引く。ただし、10で割って出た余りの下1桁が0の場合はチェック数字を0とする。)
ここで、例として ISBN 978-4-10-109205-□ のチェックディジット(□部分)を求めてみる。
9×1 + 7×3 + 8×1 + 4×3 + 1×1 + 0×3 + 1×1 + 0×3 + 9×1 + 2×3 + 0×1 + 5×3
= 9 + 21 + 8 + 12 + 1 + 0 + 1 + 0 + 9 + 6 + 0 + 15
= 82
82 ÷ 10 = 8 あまり 2
10 - 2 = 8
よって、このISBNのチェックディジットは8である。
標準入力からチェックディジットが与えられるとき、チェックディジットがその値に一致するISBNの個数を標準出力に出力してください。
※日本国内で出版されるもののみを考えるため、ISBN-10では先頭が「4」、ISBN-13では先頭が「978-4」を固定とします。
また、実際に書籍が存在するかどうかは問いません。
例えば、チェックディジットが「1」のとき、上記の条件をみたすものは14751通りあります。
【入出力サンプル】
標準入力
1
標準出力
14751
======================================================================
1. ABCD-EFGHがすべて異なる数字
2. ISBN-10では先頭が「4」、ISBN-13では先頭が「978-4」を固定
という条件つきなので,数え上げが可能。
R だと,順列生成とベクトル演算で短く書くことができる。
permutations はライブラリにあるので,隠蔽することができ,実質の関数 f はわずか 2 行ということになる。
が,しかし。これでは 0.8 秒ほど掛かる。
permutations = function(n) {
z = matrix(1)
for (i in 2:n) {
x = cbind(z, i)
a = c(1:i, 1:(i - 1))
z = matrix(0, ncol = ncol(x), nrow = i * nrow(x))
z[1:nrow(x), ] = x
for (j in 2:i - 1) {
z[j * nrow(x) + 1:nrow(x), ] = x[, a[1:i + j]]
}
}
z[, 1:(n-2)]-1
}
f = function(cd) {
a = permutations(10) # 0 ~ 9 のうちの 8 個を使った順列を生成(同じものが 2 つずつある)
cat(sum(11-(40+a %*% 9:2) %% 11 == cd & 10-(50+a %*% c(1,3,1,3,1,3,1,3)) %% 10 == cd)/2) # ISBN10 と ISBN13
}
permutations を java に移植してもよいのだが,単純に 8 重の for ループのプログラムを書く。
以下の R プログラムだと 3 秒ほどかかるので,Java に書き直して O.K.
R プログラム
f = function(cd) {
count = 0
for (i5 in 0:9) {
x5 = 50 + i5
y5 = 40 + 9 * i5
for (i6 in 0:9) {
if (i6 == i5) next
x6 = x5 + 3 * i6
y6 = y5 + 8 * i6
for (i7 in 0:9) {
if (i7 == i5 || i7 == i6) next
x7 = x6 + i7
y7 = y6 + 7 * i7
for (i8 in 0:9) {
if (i8 == i5 || i8 == i6 || i8 == i7) next
x8 = x7 + 3 * i8
y8 = y7 + 6 * i8
for (i9 in 0:9) {
if (i9 == i5 || i9 == i6 || i9 == i7 || i9 == i8) next
x9 = x8 + i9
y9 = y8 + 5 * i9
for (i10 in 0:9) {
if (i10 == i5 || i10 == i6 || i10 == i7 || i10 == i8 || i10 == i9) next
x10 = x9 + 3 * i10
y10 = y9 + 4 * i10
for (i11 in 0:9) {
if (i11 == i5 || i11 == i6 || i11 == i7 || i11 == i8 || i11 == i9 || i11 == i10) next
x11 = x10 + i11
y11 = y10 + 3 * i11
for (i12 in 0:9) {
if (i12 == i5 || i12 == i6 || i12 == i7 || i12 == i8 || i12 == i9 || i12 == i10 || i12 == i11) next
isbn13 = 10 - (x11 + 3 * i12)%%10
isbn10 = 11 - (y11 + 2 * i12)%%11
if (isbn13 == cd && isbn10 == cd) {
count = count + 1
}
}
}
}
}
}
}
}
}
cat(count)
}
system.time(f(1)) # 14751, 3.7sec.
system.time(f(2)) # 18271, 3.7sec.
system.time(f(5)) # 14549, 3.7sec.
system.time(f(7)) # 14578, 3.7sec.
system.time(f(8)) # 18358, 3.7sec.
Java プログラム
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
if (true) {
System.out.println(f(1)); // 14751
System.out.println(f(2)); // 18271
System.out.println(f(5)); // 14549
System.out.println(f(7)); // 14578
System.out.println(f(8)); // 18358
} else {
Scanner cin = new Scanner(System.in);
String line;
line = cin.nextLine();
int cd = Integer.parseInt(line);
System.out.println(f(cd));
}
}
static int f(int cd) {
int i5, i6, i7, i8, i9, i10, i11, i12;
int x5, x6, x7, x8, x9, x10, x11;
int y5, y6, y7, y8, y9, y10, y11;
int isbn10, isbn13;
int count = 0;
for (i5 = 0; i5 < 10; i5++) {
x5 = 50 + i5;
y5 = 40 + 9 * i5;
for (i6 = 0; i6 < 10; i6++) {
if (i6 == i5) continue;
x6 = x5 + 3 * i6;
y6 = y5 + 8 * i6;
for (i7 = 0; i7 < 10; i7++) {
if (i7 == i5 || i7 == i6) continue;
x7 = x6 + i7;
y7 = y6 + 7 * i7;
for (i8 = 0; i8 < 10; i8++) {
if (i8 == i5 || i8 == i6 || i8 == i7) continue;
x8 = x7 + 3 * i8;
y8 = y7 + 6 * i8;
for (i9 = 0; i9 < 10; i9++) {
if (i9 == i5 || i9 == i6 || i9 == i7 || i9 == i8) continue;
x9 = x8 + i9;
y9 = y8 + 5 * i9;
for (i10 = 0; i10 < 10; i10++) {
if (i10 == i5 || i10 == i6 || i10 == i7 || i10 == i8 || i10 == i9) continue;
x10 = x9 + 3 * i10;
y10 = y9 + 4 * i10;
for (i11 = 0; i11 < 10; i11++) {
if (i11 == i5 || i11 == i6 || i11 == i7 || i11 == i8 || i11 == i9 || i11 == i10) continue;
x11 = x10 + i11;
y11 = y10 + 3 * i11;
for (i12 = 0; i12 < 10; i12++) {
if (i12 == i5 || i12 == i6 || i12 == i7 || i12 == i8 || i12 == i9 || i12 == i10 || i12 == i11) continue;
isbn13 = 10 - (x11 + 3 * i12) % 10;
isbn10 = 11 - (y11 + 2 * i12) % 11;
if (isbn13 == cd && isbn10 == cd) {
count++;
}
}
}
}
}
}
}
}
}
return count;
}
}



















