算額（その481）

算額（その481）

宮城県丸森町小斎日向 鹿島神社 明治13年

徳竹亜紀子，谷垣美保: 2021年度の算額調査，仙台高等専門学校名取キャンパス 研究紀要，第 58 号, p.7-28, 2022.
https://www.sendai-nct.ac.jp/natori-library/wp/wp-content/uploads/2022/03/kiyo2022-2.pdf

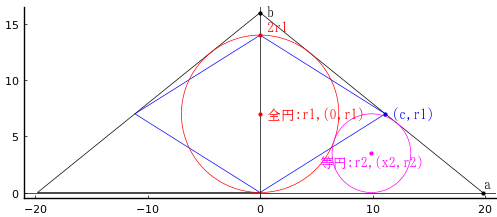
長方形内に 2 本の斜線で隔てられた領域に甲，乙，丙，丁の 4 円が入っている。甲円の直径が 12 寸のとき，乙円の直径を最大にしたい。乙円，丙円，丁円の直径を求めよ。

長方形の長辺の長さを a
甲円の半径と中心座標を r1, (a - r1, r1)
乙円の半径と中心座標を r2, (r2, r2)
丙円の半径と中心座標を r3, (x3, 2r1 - r3)
丁円の半径と中心座標を r4, (r4, y4)
とする。

乙円が最大になるのは 2 本の斜線が直交するときである。

このとき，甲円が内接する直角三角形（の半分）と，乙円，丙円，丁円の 3 個の直角三角形は相似なので，相似比は 12:6:4:3 になるのは明らかである。

長方形の長辺の長さ a，丙円と丁円の中心座標を確定するためには，以下の連立方程式を nlsolve() で解き，数値解を求める。

include("julia-source.txt");

using SymPy

@syms a::positive, b::positive, c::positive, d::positive,
     r1::positive, r2::positive, r3::positive, x3::positive,
     r4::positive, y4::positive;

eq1 = distance(0, 2r1, b, 0, a - r1, r1) - r1^2 |> simplify
eq2 = distance(0, 2r1, b, 0, r2, r2) - r2^2 |> simplify
eq3 = distance(0, 2r1, b, 0, x3, 2r1 - r3) - r3^2 |> simplify
eq4 = distance(0, 2r1, b, 0, r4, y4) - r4^2 |> simplify
eq5 = distance(0, c, d, 2r1, a - r1, r1) - r1^2 |> simplify
eq6 = distance(0, c, d, 2r1, r2, r2) - r2^2 |> simplify
eq7 = distance(0, c, d, 2r1, x3, 2r1 - r3) - r3^2 |> simplify
eq8 = distance(0, c, d, 2r1, r4, y4) - r4^2 |> simplify
eq9 = b/2r1 - (2r1 - c)/d;
# res = solve([eq1, eq2, eq3, eq4, eq5, eq6, eq7, eq8, eq9], (a, b, c, d, r2, r3, x3, r4, y4))

using NLsolve

function nls(func, params...; ini = [0.0])
   if typeof(ini) <: Number
       r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=1e-14)
       v = r.zero[1]
   else
       r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=1e-14)
       v = r.zero
   end
   return v, r.f_converged
end;

function H(u)
   (a, b, c, d, r2, r3, x3, r4, y4) = u
   return [
       4*r1^2*(a^2 - a*b - 2*a*r1 + b*r1)/(b^2 + 4*r1^2),  # eq1
       4*b*r1*(b*r1 - b*r2 - 2*r1*r2 + r2^2)/(b^2 + 4*r1^2),  # eq2
       4*r1*(-b*r3*x3 - r1*r3^2 + r1*x3^2)/(b^2 + 4*r1^2),  # eq3
       b*(4*b*r1^2 - 4*b*r1*y4 - b*r4^2 + b*y4^2 - 8*r1^2*r4 + 4*r1*r4*y4)/(b^2 + 4*r1^2),  # eq4
       (a^2*c^2 - 4*a^2*c*r1 + 4*a^2*r1^2 - 2*a*c^2*d - 2*a*c^2*r1 + 6*a*c*d*r1 + 8*a*c*r1^2 - 4*a*d*r1^2 - 8*a*r1^3 + c^2*d^2 + 2*c^2*d*r1 - 2*c*d^2*r1 - 6*c*d*r1^2 + 4*d*r1^3)/(c^2 - 4*c*r1 + d^2 + 4*r1^2),  # eq5
       d*(c^2*d - 2*c^2*r2 - 2*c*d*r2 + 4*c*r1*r2 + 2*c*r2^2 - 4*r1*r2^2)/(c^2 - 4*c*r1 + d^2 + 4*r1^2),  # eq6
       (c^2*d^2 - 2*c^2*d*x3 - c^2*r3^2 + c^2*x3^2 - 4*c*d^2*r1 + 2*c*d^2*r3 + 8*c*d*r1*x3 - 2*c*d*r3*x3 + 4*c*r1*r3^2 - 4*c*r1*x3^2 + 4*d^2*r1^2 - 4*d^2*r1*r3 - 8*d*r1^2*x3 + 4*d*r1*r3*x3 - 4*r1^2*r3^2 + 4*r1^2*x3^2)/(c^2 - 4*c*r1 + d^2 + 4*r1^2),  # eq7
       d*(c^2*d - 2*c^2*r4 - 2*c*d*y4 + 4*c*r1*r4 + 2*c*r4*y4 - d*r4^2 + d*y4^2 - 4*r1*r4*y4)/(c^2 - 4*c*r1 + d^2 + 4*r1^2),  # eq8
       b/(2*r1) - (-c + 2*r1)/d,  # eq9
   ]
end;

r1 = 12/2
iniv = [big"18.2", 9.1, 4.4, 10.3, 3.1, 2.1, 4.1, 1.6, 7.4]
res = nls(H, ini=iniv);
println(res);

   (BigFloat[17.99999999999999999999999999999958787838359120591652042567639170665603992771524, 8.99999999999999999999999999999984155332251522567635341448728327805462644595505, 4.500000000000000000000000000000024260203115491587793400726971558949746337902191, 9.99999999999999999999999999999961117790943389634414624752326251631979937803581, 2.999999999999999999999999999999520308595440307614021124672062062280275651040769, 1.999999999999999999999999999998867711776892728650702737150651030496089805787837, 3.999999999999999999999999999999609211568160356725082605146703705988921640964954, 1.499999999999999999999999999999653325970663365188170394965090885917020592201141, 7.499999999999999999999999999999917260822554019948727938965336654899285660744732], true)

   a = 18;  b =　9;  c =　4.5;  d =　10;  r1 = 6;  r2 =　3;  r3 =　2;  x3 =　4;  r4 = 1.5;  y4 = 7.5
   乙円の直径 = 6;  丙円の直径 = 4;  丁円の直径 = 3

using Plots

function draw(more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r1 = 12/2
   (a, b, c, d, r2, r3, x3, r4, y4)  = res[1]
   @printf("a = %g;  b =　%g;  c =　%g;  d =　%g;  r1 = %g;  r2 =　%g;  r3 =　%g;  x3 =　%g;  r4 = %g;  y4 = %g\n",  a, b, c, d, r1, r2, r3, x3, r4, y4)
   @printf("乙円の直径 = %g;  丙円の直径 = %g;  丁円の直径 = %g\n", 2r2, 2r3, 2r4)
   plot([0, a, a, 0, 0], [0, 0, 2r1, 2r1, 0], color=:blue, lw=0.5)
   circle(a - r1, r1, r1)
   circle(r2, r2, r2, :green)
   circle(x3, 2r1 - r3, r3, :magenta)
   circle(r4, y4, r4, :orange)
   segment(0, c, d, 2r1)
   segment(0, 2r1, b, 0)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
       point(a, 0, "a", :blue, :center, :top, delta=-1.5delta)
       point(b, 0, "b", :blue, :center, :top, delta=-1.5delta)
       point(0, c, "c ", :blue, :right, :vcenter)
       point(d, 2r1, "(d,2r1)", :blue, :center, :bottom, delta=delta)
       point(0, 2r1, "2r1 ", :blue, :right, :vcenter)
       point(a - r1, r1, "甲円:r1,(a-r1,r1)", :red, :center, :top, delta=-delta)
       point(r2, r2, "乙円:r2,(r2,r2)", :green, :center, :top, delta=-delta)
       point(x3, 2r1 - r3, "丙円:x3\n(x3,2r1-r3)", :magenta, :center, :bottom, delta=delta)
       point(r4, y4, "丁円:r4\n(r4,y4)", :orange, :center, :vcenter)
       plot!(xlims=(-1.5, 19), ylims=(-1, 13))
   else
       plot!(showaxis=false)
   end
end;

算額（その480）

算額（その480）

宮城県丸森町小斎日向 鹿島神社 明治13年

徳竹亜紀子，谷垣美保: 2021年度の算額調査，仙台高等専門学校名取キャンパス 研究紀要，第 58 号, p.7-28, 2022.
https://www.sendai-nct.ac.jp/natori-library/wp/wp-content/uploads/2022/03/kiyo2022-2.pdf

直角三角形の 2 つの辺それぞれを直径とする大半円と中半円があり，甲円 1 個，乙円 2 個が入っている。甲円の直径が 12 寸のとき，乙円の直径はいかほどか。

この問題（図）は，「算額（その373）」に1個の円（甲円）を加えたものである。

大半円の半径と中心座標を r1, (r1, 0)
中半円の半径と中心座標を r2, (0, r2)
乙円の半径と中心座標を r3, (r3, y31) および (x3, y32)
甲円の半径と中心座標を (x4, y4)
とする。

r1 を与えて甲円，乙円の比を求めればよい。
以下の連立方程式を nlsolve() で解き，数値解を求める。

include("julia-source.txt");

using SymPy

@syms r1::positive, r2::positive, r3::positive, y31::positive,
     x3::positive, y32::positive, x0::positive, y0::positive,
     r4::positive, x4::positive;

eq1 = (r1 - r3)^2 + y31^2 - (r1 + r3)^2
eq2 = (r1 - x3)^2 + y32^2 - (r1 - r3)^2
eq3 = x3^2 + (r2 - y32)^2 - (r2 - r3)^2
eq4 = sqrt(x0^2 + y0^2) * sqrt(4r1^2 + 4r2^2) - 2r1*2r2
eq5 = (x0^2 + y0^2)/((2r1 - x0)^2 + y0^2) - r2^2/r1^2
eq6 = y0/(2r1 - x0) - r2/r1
eq7 = distance(0, 2r2, 2r1, 0, r3, y31) - r3^2
eq8 = distance(0, 2r2, 2r1, 0, x4, r4) - r4^2
eq9 = x4^2 + (r2 - r4)^2 - (r2 + r4)^2;
# res = solve([eq1, eq2, eq3, eq4, eq5, eq6, eq7, eq8, eq9])

using NLsolve

function nls(func, params...; ini = [0.0])
   if typeof(ini) <: Number
       r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=1e-14)
       v = r.zero[1]
   else
       r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=1e-14)
       v = r.zero
   end
   return v, r.f_converged
end;

function H(u)
   (r2, r3, x3, y31, y32, x0, y0, r4, x4) = u
   return [
     y31^2 + (r1 - r3)^2 - (r1 + r3)^2,  # eq1
     y32^2 - (r1 - r3)^2 + (r1 - x3)^2,  # eq2
     x3^2 - (r2 - r3)^2 + (r2 - y32)^2,  # eq3
     -4*r1*r2 + sqrt(4*r1^2 + 4*r2^2)*sqrt(x0^2 + y0^2),  # eq4
     (x0^2 + y0^2)/(y0^2 + (2*r1 - x0)^2) - r2^2/r1^2,  # eq5
     y0/(2*r1 - x0) - r2/r1,  # eq6
     -r3^2 + (-r1*(r1*r3 + 2*r2^2 - r2*y31)/(r1^2 + r2^2) + r3)^2 + (-r2*(2*r1^2 - r1*r3 + r2*y31)/(r1^2 + r2^2) + y31)^2,  # eq7
     -r4^2 + (-r1*(r1*x4 + 2*r2^2 - r2*r4)/(r1^2 + r2^2) + x4)^2 + (-r2*(2*r1^2 - r1*x4 + r2*r4)/(r1^2 + r2^2) + r4)^2,  # eq8
     x4^2 + (r2 - r4)^2 - (r2 + r4)^2,  # eq9
   ]
end;

r1 = 2
iniv = [big"0.74", 0.25, 0.43, 0.99, 0.50, 0.70, 0.96, 0.3, 0.9] .* r1
res = nls(H, ini=iniv);
println(res);
   (BigFloat[1.499995633106604731106217565251734298641076539651459792549110396918372067553379, 0.4999982532417265457675464027354950113622544897882557074519749874135711945879507, 0.800866578143091303247385619338396311792275188093891061234446679226046049456078, 1.999996506480401921739553582868335698220584759521935908625272734584033846236077, 0.9011571876557469862028001006549259506532077100910750639519068447933844446163861, 1.439994633957959074699642274497938890026647403738597804177827679741963010273783, 1.919998434896268283017600823067951959817724789545466231142528151823621455686963, 0.6666662784960143361820323670588178708216293099954384020479610896596640225195141, 1.999996506480401921739553582868335696584057211851391847198799255502987101477975], true)

   r1 = 2;  r2 =　1.5;  r3 =　0.499998;  x3 =　0.800867;  y31 =　2;  y32 =　0.901157;  x0 =　1.43999;  y0 = 1.92;  r4 = 0.666666;  x4 = 2
   乙円の直径は甲円の直径の 0.749998 倍である。

大円の半径 r1 = 2 としたとき，乙円の直径は甲円の直径の 0.7499978165533023 倍である。
ちなみにこの比は，r2/r1 と同じである。

このとき，直角三角形の辺の長さの比は 3:4:5 になる。
しかし，r1 が 2 より大きい場合や小さい場合には直角三角形の辺の長さの比は微妙に異なる。
本来，r1 が異なっても図はすべて相似になるべきなので，このような現象は理解し難いが，数値計算上の精度の問題であろう。

したがって，「術: 乙円の直径は甲円の直径の 3/4 倍である」という記述は正しいものと思われる。

Float64(res[1][2]/res[1][8]) |> println
Float64(res[1][1]/r1) |> println

   0.7499978165533023
   0.7499978165533023

using Plots

function draw(more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r2, r3, x3, y31, y32, x0, y0, r4, x4)  = res[1]
   @printf("r1 = %g;  r2 =　%g;  r3 =　%g;  x3 =　%g;  y31 =　%g;  y32 =　%g;  x0 =　%g;  y0 = %g;  r4 = %g;  x4 = %g\n",  r1, r2, r3, x3, y31, y32, x0, y0, r4, x4)
   @printf("乙円の直径は甲円の直径の %g 倍である。\n", r3/r4)
   plot()
   circle(r1, 0, r1, beginangle=0, endangle=180)
   circle(0, r2, r2, :blue, beginangle=-90, endangle=90)
   circle(x3, y32, r3, :green)
   circle(r3, y31, r3, :green)
   circle(x4, r4, r4, :orange)
   segment(0, 2r2, 2r1, 0, :black)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       point(r1, 0, " r1", :red, :left, :bottom, delta=delta/2)
       point(0, r2, " r2", :blue, :left, :vcenter)
       point(r3, y31, "(r3,y31)", :green, :center, delta=-delta/2)
       point(x3, y32, "(x3,y32)", :green, :center, delta=-delta/2)
       point(x4, r4, "甲円:r4,(x4,r4)", :orange, :center, delta=-delta/2)
       point(x0, y0, "  (x0,y0)", :green, :left, :vcenter, delta=-delta/2)
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
   else
       plot!(showaxis=false)
   end
end;

算額（その479）

算額（その479）

宮城県丸森町小斎日向 鹿島神社 明治9年

徳竹亜紀子，谷垣美保: 2021年度の算額調査，仙台高等専門学校名取キャンパス 研究紀要，第 58 号, p.7-28, 2022.
https://www.sendai-nct.ac.jp/natori-library/wp/wp-content/uploads/2022/03/kiyo2022-2.pdf

外円内に甲，乙，丙，丁円が入っている。丁円の直径を知って，丙円の直径を求めよ。

甲円の半径と中心座標を r1, (x1, y1)
乙円の半径と中心座標を r2, (0, r2), (0, r0 - r2)
丙円の半径と中心座標を r3, (x3, r3)
丁円の半径と中心座標を r4, (x4, r4)
とおいて以下の連立方程式の数値解を求める。

include("julia-source.txt")

using SymPy
@syms r1::positive, x1::positive, y1::positive, r2::positive,
     r3::positive, x3::positive, r4::positive,
     x4::positive, r0::positive;
r0 = 4r2
y1 = 2r2
r4 = 1//2
eq1 = x1^2 + y1^2 - (r0 - r1)^2
eq2 = x3^2 + r3^2 - (r0 - r3)^2
eq3 = x1^2 + (r0 - r2 - y1)^2 - (r1 + r2)^2
eq4 = (x3 - x1)^2 + (y1 - r3)^2 - (r1 + r3)^2
eq5 = (x1 - x4)^2 + (y1 - r4)^2 - (r1 + r4)^2
eq6 = x4^2 + (r2 - r4)^2 - (r2 + r4)^2;
# res = solve([eq1, eq2, eq3, eq4, eq5, eq6])#, (r1, x1, r2, r3, x3, x4))

using NLsolve

function nls(func, params...; ini = [0.0])
   if typeof(ini) <: Number
       r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=big"1e-40")
       v = r.zero[1]
   else
       r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=big"1e-40")
       v = r.zero
   end
   return v, r.f_converged
end;

function H(u)
   (r1, x1, r2, r3, x3, x4) = u
   return [
       4*r2^2 + x1^2 - (-r1 + 4*r2)^2,  # eq1
       r3^2 + x3^2 - (4*r2 - r3)^2,  # eq2
       r2^2 + x1^2 - (r1 + r2)^2,  # eq3
       -(r1 + r3)^2 + (2*r2 - r3)^2 + (-x1 + x3)^2,  # eq4
       -(r1 + r4)^2 + (2*r2 - r4)^2 + (x1 - x4)^2,  # eq5
       x4^2 + (r2 - r4)^2 - (r2 + r4)^2,  # eq6
   ]
end;

r0 = 4r2
y1 = 2r2
r4 = 1/2

iniv = [big"2.6", 4.3, 2.2, 1.5, 7.1, 3.0]
res = nls(H, ini=iniv)

  (BigFloat[1.311396103067892771960759925894364135356352343919626632929505882095829615307969, 2.141500868793756520305245638521174546550359518581729934628195842934091980001108, 1.092830085889910643300633271578636779463626953266355527441254901746524679423308, 0.7285533905932737622004221810524245196424179688442370182941699344976831196155384, 3.569168114656260867175409397535290910917265864302883224380326404890153300001858, 1.478397839480233171313044189429409031462889497069357846136076631538706602818749], true)

   r1 = 1.3114;  x1 = 2.1415;  r2 = 1.09283;  r3 = 0.728553;  x3 = 3.56917;  x4 = 1.4784
   丙円の直径は丁円の直径の 1.45711 倍

丙円の半径は丁円の半径の 1.4571067811865475 倍である。
この数値は術によれば sqrt(1/2)+3/4 である。

Float64(res[1][4]/r4) |> println
sqrt(1/2)+3/4 |> println

   1.4571067811865475
   1.4571067811865475

using Plots

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r1, x1, r2, r3, x3, x4) = res[1]
   r0 = 4r2
   y1 = 2r2
   r4 = 1/2
   @printf("r1 = %g;  x1 = %g;  r2 = %g;  r3 = %g;  x3 = %g;  x4 = %g\n", r1, x1, r2, r3, x3, x4)
   @printf("丙円の直径は丁円の直径の %g 倍\n", r3/r4)
   plot()
   circle(0, 0, 4r2, :black)
   circle4(x1, y1, r1, :magenta)
   circle(0, r0 - r2, r2, :blue)
   circle(0, r2 - r0, r2, :blue)
   circle(0, r2, r2, :blue)
   circle(0, -r2, r2, :blue)
   circle4(x3, r3, r3, :green)
   circle4(x4, r4, r4, :orange)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /  3  # size[2] * fontsize * 2
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
       point(x1, y1, "甲円:r1,(x1,y1)", :magenta, :center, :top, delta=-delta/2)
       point(0, r0 - r2, " 乙円:r2,(0,r0-r2)", :blue, :left, :vcenter)
       point(0, r2, " 乙円:r2,(0,r2)", :blue, :left, :vcenter)
       point(x3, r3, "丙円::r3,(x3,r3) ", :green, :right, :vcenter)
       point(x4, r4, " 丁円::r4,(x4,r4) ", :orange, :left, :top, delta=-delta/2)
       point(0, r0, " r0", :black, :left, :bottom, delta=delta/3)
   end
end;

 

算額（その478）

算額（その478）

宮城県丸森町小斎日向 鹿島神社 明治9年

徳竹亜紀子，谷垣美保: 2021年度の算額調査，仙台高等専門学校名取キャンパス 研究紀要，第 58 号, p.7-28, 2022.
https://www.sendai-nct.ac.jp/natori-library/wp/wp-content/uploads/2022/03/kiyo2022-2.pdf

鈎股弦があり，鈎，股，弦を直径としその中点を中心とする 3 個の円，天円，地円，人円がある。
天円の中に星円があり，星園は人円，地円と外接し，天円に内接する。
地円，人円の直径を知って星円の直径を求めよ。

地円の直径は股，人円の直径は鈎である。
天円の半径と中心座標を r1, (r2, r3)
地円の半径と中心座標を r2, (r2, 0)
人円の半径と中心座標を r3, (0, r3)
星円の半径と中心座標を r4, (x4, y4)
とおいて以下の連立方程式を解く。

include("julia-source.txt")

using SymPy
@syms 鈎::positive, 股::positive, 弦::positive,
     r1::positive, r2::positive, r3::positive,
     r4::positive, x4::positive, y4::positive;

r1 = sqrt(鈎^2 + 股^2)/2
(r2, r3) = (股, 鈎).//2;

eq1 = (r2 - x4)^2 + (y4 - r3)^2 - (r1 - r4)^2
eq2 = (r2 - x4)^2 + y4^2 - (r2 + r4)^2
eq3 = x4^2 + (y4 - r3)^2 - (r3 + r4)^2
res = solve([eq1, eq2, eq3], (r4, x4, y4))

   1-element Vector{Tuple{Sym, Sym, Sym}}:
    (股^2*鈎^2*(4*股^3 + 2*股^2*鈎 + 4*股^2*sqrt(股^2 + 鈎^2) + 3*股*鈎^2 + 2*股*鈎*sqrt(股^2 + 鈎^2) + 鈎^3 + 鈎^2*sqrt(股^2 + 鈎^2))/(8*股^6 + 8*股^5*sqrt(股^2 + 鈎^2) + 8*股^4*鈎^2 + 4*股^3*鈎^3 + 4*股^3*鈎^2*sqrt(股^2 + 鈎^2) + 5*股^2*鈎^4 + 4*股^2*鈎^3*sqrt(股^2 + 鈎^2) + 4*股*鈎^5 + 4*股*鈎^4*sqrt(股^2 + 鈎^2) + 2*鈎^6 + 2*鈎^5*sqrt(股^2 + 鈎^2)), 股*鈎^2*(4*股^4 + 6*股^3*鈎 + 4*股^3*sqrt(股^2 + 鈎^2) + 7*股^2*鈎^2 + 6*股^2*鈎*sqrt(股^2 + 鈎^2) + 5*股*鈎^3 + 5*股*鈎^2*sqrt(股^2 + 鈎^2) + 2*鈎^4 + 2*鈎^3*sqrt(股^2 + 鈎^2))/(8*股^6 + 8*股^5*sqrt(股^2 + 鈎^2) + 8*股^4*鈎^2 + 4*股^3*鈎^3 + 4*股^3*鈎^2*sqrt(股^2 + 鈎^2) + 5*股^2*鈎^4 + 4*股^2*鈎^3*sqrt(股^2 + 鈎^2) + 4*股*鈎^5 + 4*股*鈎^4*sqrt(股^2 + 鈎^2) + 2*鈎^6 + 2*鈎^5*sqrt(股^2 + 鈎^2)), 股^2*鈎*(4*股^3 + 2*股^2*鈎 + 4*股^2*sqrt(股^2 + 鈎^2) + 3*股*鈎^2 + 2*股*鈎*sqrt(股^2 + 鈎^2) + 鈎^3 + 鈎^2*sqrt(股^2 + 鈎^2))/(4*股^5 + 4*股^4*sqrt(股^2 + 鈎^2) + 3*股^3*鈎^2 + 2*股^2*鈎^3 + 股^2*鈎^2*sqrt(股^2 + 鈎^2) + 2*股*鈎^4 + 2*股*鈎^3*sqrt(股^2 + 鈎^2) + 2*鈎^5 + 2*鈎^4*sqrt(股^2 + 鈎^2)))

星円の半径のみならず中心座標も大変長い式になる。
鈎 = 3，股 = 4 のとき，星円の直径は 2 になる。

2res[1][1](鈎 => 3, 股 => 4) |> println

   2

   星円の直径 = 2;  r1 = 2.5;  r2 = 2;  r3 = 1.5;  r4 = 1;  x4 = 2;  y4 = 3

using Plots

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (鈎, 股) = (3, 4)
   r1 = sqrt(鈎^2 + 股^2)/2
   (r2, r3) = (股, 鈎).//2
   (r4, x4, y4) = (股^2*鈎^2*(4*股^3 + 2*股^2*鈎 + 4*股^2*sqrt(股^2 + 鈎^2) + 3*股*鈎^2 + 2*股*鈎*sqrt(股^2 + 鈎^2) + 鈎^3 + 鈎^2*sqrt(股^2 + 鈎^2))/(8*股^6 + 8*股^5*sqrt(股^2 + 鈎^2) + 8*股^4*鈎^2 + 4*股^3*鈎^3 + 4*股^3*鈎^2*sqrt(股^2 + 鈎^2) + 5*股^2*鈎^4 + 4*股^2*鈎^3*sqrt(股^2 + 鈎^2) + 4*股*鈎^5 + 4*股*鈎^4*sqrt(股^2 + 鈎^2) + 2*鈎^6 + 2*鈎^5*sqrt(股^2 + 鈎^2)), 股*鈎^2*(4*股^4 + 6*股^3*鈎 + 4*股^3*sqrt(股^2 + 鈎^2) + 7*股^2*鈎^2 + 6*股^2*鈎*sqrt(股^2 + 鈎^2) + 5*股*鈎^3 + 5*股*鈎^2*sqrt(股^2 + 鈎^2) + 2*鈎^4 + 2*鈎^3*sqrt(股^2 + 鈎^2))/(8*股^6 + 8*股^5*sqrt(股^2 + 鈎^2) + 8*股^4*鈎^2 + 4*股^3*鈎^3 + 4*股^3*鈎^2*sqrt(股^2 + 鈎^2) + 5*股^2*鈎^4 + 4*股^2*鈎^3*sqrt(股^2 + 鈎^2) + 4*股*鈎^5 + 4*股*鈎^4*sqrt(股^2 + 鈎^2) + 2*鈎^6 + 2*鈎^5*sqrt(股^2 + 鈎^2)), 股^2*鈎*(4*股^3 + 2*股^2*鈎 + 4*股^2*sqrt(股^2 + 鈎^2) + 3*股*鈎^2 + 2*股*鈎*sqrt(股^2 + 鈎^2) + 鈎^3 + 鈎^2*sqrt(股^2 + 鈎^2))/(4*股^5 + 4*股^4*sqrt(股^2 + 鈎^2) + 3*股^3*鈎^2 + 2*股^2*鈎^3 + 股^2*鈎^2*sqrt(股^2 + 鈎^2) + 2*股*鈎^4 + 2*股*鈎^3*sqrt(股^2 + 鈎^2) + 2*鈎^5 + 2*鈎^4*sqrt(股^2 + 鈎^2)))
   @printf("星円の直径 = %g;  r1 = %g;  r2 = %g;  r3 = %g;  r4 = %g;  x4 = %g;  y4 = %g\n", 2r4, r1, r2, r3, r4, x4, y4)
   plot([0, 股, 0, 0], [0, 0, 鈎, 0], color=:blue, lw=0.5)
   circle(r2, r3, r1)
   circle(r2, 0, r2, :magenta)
   circle(0, r3, r3, :green)
   circle(x4, y4, r4, :orange)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /  3  # size[2] * fontsize * 2
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
       point(r2, r3, " 天円:r1,(r2,r3)", :red, :left, :top, delta=-delta)
       point(r2, 0, " 地円:r2,(r2,0)", :magenta, :left, :top, delta=-delta)
       point(0, r3, " 人円:r3,(0,r3)", :green, :left, :top, delta=-delta)
       point(x4, y4, " 星円:r4,(x4,y4)", :orange, :left, :top, delta=-delta)
   end
end;

算額（その477）

算額（その477）

宮城県丸森町小斎日向 鹿島神社 明治9年

徳竹亜紀子，谷垣美保: 2021年度の算額調査，仙台高等専門学校名取キャンパス 研究紀要，第 58 号, p.7-28, 2022.
https://www.sendai-nct.ac.jp/natori-library/wp/wp-content/uploads/2022/03/kiyo2022-2.pdf

円内に等円 2 個，菱形 2 個が入っている。等円の直径が与えられたとき，菱形の一辺の長さを求めよ。

菱形の短い方の対角線の長さを 2a，長い方の対角線の長さを 2b とする。菱形の右の頂点の座標は (b, 2r - a) である。頂点は円周上にあるので，b = sqrt((2r)^2 - (2r - a)^2) である。

以下の方程式で a を求める。

include("julia-source.txt")

using SymPy
@syms a::positive, b::positive, r::positive;

b = sqrt((2r)^2 - (2r - a)^2)
eq = distance(0, 2r - 2a, b, 2r - a, r, 0) - r^2
res = solve(eq, a);

6 個の解が得られるが，2 番目のものが適解である。

すなわち，a = r*(2 - √7/2) である。

res[2] |> println

   r*(2 - sqrt(7)/2)

菱形の一辺の長さは sqrt(a^2 + b^2) = r*(√7 - 1) である。

@syms a::positive, b::positive, r::positive;
a = r*(2 - sqrt(Sym(7))/2)
b = sqrt((2r)^2 - (2r - a)^2)
sqrt(a^2 + b^2) |> simplify |> sympy.sqrtdenest |> println

   r*(-1 + sqrt(7))

等円の直径が 1 寸のとき，菱形の一辺の長さは 0.5(√7 - 1) = 0.8228756555322954 = 8分2厘2毛8糸有奇である。

0.5(√7 - 1) |> println

   0.8228756555322954

using Plots

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r = 1//2
   a = r*(2 - sqrt(7)/2)
   b = sqrt((2r)^2 - (2r - a)^2)
   length = r*(sqrt(7) - 1)
   @printf("a = %g; b = %g;  菱形の一辺の長さ = %g\n", a, b, length)
   plot([0, b,  0, -b, 0], [2r - 2a, 2r - a, 2r, 2r - a, 2r - 2a], color=:brown, lw=0.5)
   plot!([0, b,  0, -b, 0], [2a - 2r, a - 2r, -2r, a - 2r, 2a - 2r], color=:brown, lw=0.5)
   circle(0, 0, 2r, :blue)
   circle(r, 0, r)
   circle(-r, 0, r)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /  3  # size[2] * fontsize * 2
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
       point(0, 2r, " 2r", :blue, :left, :bottom, delta=delta/2)
       point(0, 2r - a, " 2r-a", :brown, :left, :bottom, delta=delta/2)
       point(b, 2r - a, "(b,2r-a)", :brown, :left, :bottom, delta=delta/2)
       point(0, 2r - 2a, " 2r-2a", :black, :left, :top)
       point(r, 0, "等円:r,(r,0)", :red, :center, :bottom, delta=delta)
   end
end;

算額（その476）

算額（その476）

宮城県丸森町小斎日向 鹿島神社 弘化5年

徳竹亜紀子，谷垣美保: 2021年度の算額調査，仙台高等専門学校名取キャンパス 研究紀要，第 58 号, p.7-28, 2022.
https://www.sendai-nct.ac.jp/natori-library/wp/wp-content/uploads/2022/03/kiyo2022-2.pdf

鈎股弦があり，鈎，股，弦を直径としその中点を中心とする 3 個の円，天円，地円，人円がある。
鈎股弦に内接する全円と，同じ直径を持つもう 1 つの全円は人円，地円，甲円に外接し，天円に内接している。
甲円は全円，地円と外接し，天円と内接している。
乙円は人円と地円の交わる部分にあり，人円と地円に内接する。

乙円の直径が与えられたとき，甲円の直径を求めよ。

鈎股弦は算額の写真を私が測定したところ，各辺が 3:4:5 の直角三角形と推測できる。

鈎, 股, 弦 の長さを 6, 8, 10 とする（偶数になるように設定する）
甲円の半径と中心座標を (r1, x1, y1)
乙円の半径と中心座標を (r2, x2, y2)
天円の半径と中心座標を (r3, x3, y3) = (弦/2, 股/2, 鈎/2)
地円の半径と中心座標を (r4, x4, |y4) = (股/2, 股/2, 0)
人円の半径と中心座標を (r5, x5, y5) = (鈎/2, 0, 鈎/2)
全円の半径と中心座標を (r6, x6, y6) = ((鈎 + 股 - 弦)/2, 鈎 + 股 - 弦)/2, 鈎 + 股 - 弦)/2)
とおいて以下の連立方程式を解く。

以下の連立方程式は条件が 7 個，未知数が 8 個なので，乙円の直径は一意に定まらない。
そこで，乙円の直径が最大になるときの解を求めるため，r1, x1, y1, x, y, r2, x2 について求めるが，それぞれは y3 を変数として含む式で表される。

include("julia-source.txt")

using SymPy
@syms 鈎::positive, 股::positive, 弦::positive,
     r1::positive, x1::positive, y1::positive,
     r2::positive, x2::positive, y2::positive,
     r3::positive, x3::positive, y3::positive,
     r4::positive, x4::positive, y4::positive,
     r5::positive, x5::positive, y5::positive,
     r6::positive, x6::positive, y6::positive,
     x::positive, y::positive;
(鈎, 股, 弦) = (3, 4, 5).*2
(r3, x3, y3) = (弦//2, 股//2, 鈎//2)  # 天円
(r4, x4, y4) = (股//2, 股//2, 0)  # 地円
(r5, x5, y5) = (鈎//2, 0, 鈎//2)  # 人円
(r6, x6, y6) = fill((鈎 + 股 - 弦)//2, 3)  # 全円
eq1 = (x1 - x3)^2 + (y1 - y3)^2 - (r3 - r1)^2
eq2 = (x1 - x4)^2 + y1^2 - (r1 + r4)^2
eq3 = (x1 - x)^2 + (y1 - y)^2 - (r1 + r6)^2
eq4 = (x - x4)^2 + y^2 - (r6 + r4)^2
eq5 = (x - x3)^2 + (y - y3)^2 - (r3 - r6)^2
eq6 = (x4 - x2)^2 + y2^2 - (r4 - r2)^2
eq7 = x2^2 + (y5 - y2)^2  - (r5 - r2)^2

res = solve([eq1, eq2, eq3, eq4, eq5, eq6, eq7], (r1, x1, y1, x, y, r2, x2))

   4-element Vector{NTuple{7, Sym}}:
    (3/2, 4 - sqrt(10), 9/2, 4, 6, y2/5 - 8*sqrt(6)*sqrt(y2^2 - 3*y2 + 6)/15 + 16/5, 4*y2/5 - 2*sqrt(6)*sqrt(y2^2 - 3*y2 + 6)/15 + 4/5)
    (3/2, 4 - sqrt(10), 9/2, 4, 6, y2/5 + 8*sqrt(6)*sqrt(y2^2 - 3*y2 + 6)/15 + 16/5, 4*y2/5 + 2*sqrt(6)*sqrt(y2^2 - 3*y2 + 6)/15 + 4/5)
    (3/2, sqrt(10) + 4, 9/2, 4, 6, y2/5 - 8*sqrt(6)*sqrt(y2^2 - 3*y2 + 6)/15 + 16/5, 4*y2/5 - 2*sqrt(6)*sqrt(y2^2 - 3*y2 + 6)/15 + 4/5)
    (3/2, sqrt(10) + 4, 9/2, 4, 6, y2/5 + 8*sqrt(6)*sqrt(y2^2 - 3*y2 + 6)/15 + 16/5, 4*y2/5 + 2*sqrt(6)*sqrt(y2^2 - 3*y2 + 6)/15 + 4/5)

4 組の解が求まるが，3 番目のものが適解である。r2 はその 6 番目で，y2/5 - 8*sqrt(6)*sqrt(y2^2 - 3*y2 + 6)/15 + 16/5 である。

res[3][6] |> println

   y2/5 - 8*sqrt(6)*sqrt(y2^2 - 3*y2 + 6)/15 + 16/5

この式は，y2 についての微分の式が 0 のとき，r2 が最大値を取ることを意味している。

pyplot(size=(400, 400), grid=false, aspectratio=:none, label="", fontfamily="IPAMincho")
plot(res[1][6], xlabel="y2", ylabel="r2", xlims=(0, 4))

r2 が最大値を取るときの y2 を求める。

solve(diff(res[3][6]))[1] |> println

   9/5

y2 = 9/5 のとき，r2 が最大値を取る。そのときの実際の r2 は，以下で求められるように r2 = 1 である。

つまり，「鈎, 股, 弦 の長さを 6, 8, 10 とすると」乙円の半径は 1 である。

res[3][6](y2 => 9//5) |> println

   1

甲円の半径は 3/2 である。つまり，甲円の直径は乙円の直径の 1.5 倍である。

res[3][1](y2 => 9//5) |> println

   3/2

   天円: r3 = 5;  x3 = 4;  y3 = 3
   地円: r4 = 4;  x4 = 4;  y4 = 0
   人円: r5 = 3;  x5 = 0;  y5 = 3
   全円: r6 = 2;  x6 = 2;  y6 = 2  x = 4;  y = 6
   甲円: r1 = 1.5;  x1 = 7.16228;  y1 = 4.5
   乙円: r2 = 1;  x2 = 1.6;  y2 = 1.8

using Plots

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (鈎, 股, 弦) = (3, 4, 5).*2
   (r3, x3, y3) = (弦/2, 股/2, 鈎/2)  # 天円
   (r4, x4, y4) = (股/2, 股/2, 0)  # 地円
   (r5, x5, y5) = (鈎/2, 0, 鈎/2)  # 人円
   (r6, x6, y6) = fill((鈎 + 股 - 弦)/2, 3)  # 全円
   y2 = 9/5
   (r1, x1, y1, x, y, r2, x2) = (3/2, sqrt(10) + 4, 9/2, 4, 6, y2/5 - 8*sqrt(6)*sqrt(y2^2 - 3*y2 + 6)/15 + 16/5, 4*y2/5 - 2*sqrt(6)*sqrt(y2^2 - 3*y2 + 6)/15 + 4/5)
   @printf("天円: r3 = %g;  x3 = %g;  y3 = %g\n", r3, x3, y3)
   @printf("地円: r4 = %g;  x4 = %g;  y4 = %g\n", r4, x4, y4)
   @printf("人円: r5 = %g;  x5 = %g;  y5 = %g\n", r5, x5, y5)
   @printf("全円: r6 = %g;  x6 = %g;  y6 = %g  x = %g;  y = %g\n", r6, x6, y6, x, y)
   @printf("甲円: r1 = %g;  x1 = %g;  y1 = %g\n", r1, x1, y1)
   @printf("乙円: r2 = %g;  x2 = %g;  y2 = %g\n", r2, x2, y2)
   plot([0, 股, 0, 0], [0, 0, 鈎, 0], color=:blue, lw=0.5)
   circle(x3, y3, r3)
   circle(x4, y4, r4, :blue)
   circle(x5, y5, r5, :green)
   circle(x6, y6, r6, :magenta)
   circle(x1, y1, r1, :orange)
   circle(x, y, r6, :magenta)
   circle(x2, y2, r2, :black)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /  3  # size[2] * fontsize * 2
       point(x1, y1, " 甲円:r1,(x1,y1)", :orange, :center, :bottom, delta=delta)
       #point(x2, y2, "乙円:r2,(x2,y2)", :orange, :center, :bottom, delta=delta)
       point(x3, y3, " 天円:r3,(x3, y3)", :red, :left, :bottom, delta=delta)
       point(x4, 0, "地円:r4,(x4, 0)", :blue, :center, :top, delta=-delta)
       point(0, y5, "人円:r5,(0,y5) ", :green, :right, :bottom, delta=delta)
       point(x6, y6, " 全円:r6,(x6,y6)", :magenta, :left, :bottom)
       point(x, y, "全円:r6,(x,y)", :magenta, :center, :bottom, delta=delta)
       point(x2, y2, " 乙円:r2,(x2,y2)", :black, :left, :top)
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
   end
end;

算額（その475）

算額（その475）

宮城県石巻市雄勝町 葉山神社 明治17年(1884)

徳竹亜紀子，谷垣美保: 2021年度の算額調査，仙台高等専門学校名取キャンパス 研究紀要，第 58 号, p.7-28, 2022.
https://www.sendai-nct.ac.jp/natori-library/wp/wp-content/uploads/2022/03/kiyo2022-2.pdf

外円内に同じ大きさの菱形 2 個と円が入っている。円の直径が 1 寸のとき外円の直径はいかほどか。

外円の半径と中心座標を r0, (0, 0)
菱形の長い方の対角線と短い方の対角線の長さを 2b, 2a
円の半径と中心座標を r1, (x1, y1)
とおき，以下の連立方程式を解く。

include("julia-source.txt")

using SymPy
@syms r0::positive, a::positive, b::positive,
     r1::positive, x1::positive, y1::positive;

eq1 = 2a + 2b - 2r0
eq2 = (r0 - a)^2 + b^2 - r0^2
eq3 = x1^2 + y1^2 - (r0 - r1)^2
eq4 = distance(0, r0 - 2a, b, r0 - a, x1, y1) - r1^2
eq5 = distance(0, r0 - 2a, a, b - r0, x1, y1) - r1^2;

a, b は r0 が分かれば決まる。しかし，r0, x1, y1 は SymPy では有限の時間内に計算できないようなので，a, b も含めて数値解を求める。

solve([eq1, eq2], (a, b))

   1-element Vector{Tuple{Sym, Sym}}:
    (-sqrt(2)*r0/2 + r0, sqrt(2)*r0/2)

using NLsolve

function nls(func, params...; ini = [0.0])
   if typeof(ini) <: Number
       r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=big"1e-40")
       v = r.zero[1]
   else
       r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=big"1e-40")
       v = r.zero
   end
   return v, r.f_converged
end;

function H(u)
   (r0, a, b, x1, y1) = u
   return [
       2*a + 2*b - 2*r0,  # eq1
       b^2 - r0^2 + (-a + r0)^2,  # eq2
       x1^2 + y1^2 - (r0 - r1)^2,  # eq3
       -r1^2 + (y1 - (a^2*y1 - 2*a*b^2 + a*b*x1 + b^2*r0)/(a^2 + b^2))^2 + (-b*(2*a^2 - a*r0 + a*y1 + b*x1)/(a^2 + b^2) + x1)^2,  # eq4
       -r1^2 + (y1 - (-a*(2*a^2 - a*r0 - 2*a*x1 + a*y1 - b*x1 + 2*r0*x1) + y1*(5*a^2 + 4*a*b - 8*a*r0 + b^2 - 4*b*r0 + 4*r0^2))/(5*a^2 + 4*a*b - 8*a*r0 + b^2 - 4*b*r0 + 4*r0^2))^2 + (-a*(4*a^2 + 2*a*b - 6*a*r0 + a*x1 + 2*a*y1 - b*r0 + b*y1 + 2*r0^2 - 2*r0*y1)/(5*a^2 + 4*a*b - 8*a*r0 + b^2 - 4*b*r0 + 4*r0^2) + x1)^2,  # eq5
   ]
end;

r1 = 1//2
iniv = [big"85", 25, 60, 48, 34] ./ 37
iniv = [big"2.297", 0.676, 1.622, 1.297, 0.919]
res = nls(H, ini=iniv);

   外円の直径 = 2.38017;  r0 = 1.19008;    a = 0.348568;  b = 0.841517;  x1= 0.653281;  y1= 0.222351

外円の直径は 2寸3分8毛有奇である。

using Plots

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r1 = 1//2
   (r0, a, b, x1, y1) = res[1]
   @printf("外円の直径 = %g;  r0 = %g;    a = %g;  b = %g;  x1= %g;  y1= %g\n", 2r0, r0, a, b, x1, y1)
   plot([0, b, 0, -b, 0], [r0 - 2a, r0 - a, r0, r0 - a, r0 - 2a], color=:blue, lw=0.5)
   plot!([0, a, 0, -a, 0], [-r0, b - r0, r0 - 2a, b - r0, -r0], color=:blue, lw=0.5)
   circle(0, 0, r0, :magenta)
   circle(x1, y1, r1)
   circle(-x1, y1, r1)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /  3  # size[2] * fontsize * 2
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
       point(0, r0, " r0", :magenta, :left, :bottom, delta=delta/2)
       point(0, -r0, " -r0", :magenta, :left, :top)
       point(0, r0 - a, " r0-a", :blue, :left, :vcenter)
       point(b, r0 - a, "(b,r0-a)  ", :blue, :right, :vcenter)
       point(0, r0 - 2a, " r0-2a", :blue, :left, :vcenter)
       point(0, b - r0, " b-r0", :blue, :left, :vcenter)
       point(a, b - r0, " (a,b-r0)", :blue, :left, :vcenter)
       point(x1, y1, "等円:r1,(x1,y1)", :red, :center, :top, delta=-delta)
   end
end;

 

算額（その474）

算額（その474）

宮城県石巻市雄勝町 葉山神社 明治17年(1884)

徳竹亜紀子，谷垣美保: 2021年度の算額調査，仙台高等専門学校名取キャンパス 研究紀要，第 58 号, p.7-28, 2022.
https://www.sendai-nct.ac.jp/natori-library/wp/wp-content/uploads/2022/03/kiyo2022-2.pdf

正方形の中に三角形（圭），大円，天円，小円が入っている。小円の直径が 1 寸のとき，大円の直径を求めよ。

正方形の一辺の長さを 2a
大円の半径と中心座標を r1, (r1, 0), (0, r1)
小円の半径と中心座標を r2, (0, 0)
天円の半径と中心座標を r3, (a - r3, y3)
とおき，以下の連立方程式を解く。

include("julia-source.txt")

using SymPy
@syms a::positive, r1::positive, r2::positive,
     r3::positive, y3::positive;

eq1 = (r1 - r3)^2 + y3^2 - (r1 + r3)^2
eq2 = distance(0, 2r1 - a, a, a, a - r1, 0) - r1^2
eq3 = (a - 2r1)*a/sqrt((2a - 2r1)^2 + a^2) - r2
eq4 = (a - y3)*r1 - r3*a;

どういうわけか，一度に全部の解を求めようとすると y3 が求まらない（すべての解の式に y3 が含まれ，y3 は未知数のまま）。
そこで，まず a, r1 を求め，次にそれを既知として r3, y3 を求める。
問では r2 が与えられているが，算額の常套手段で，r2 は未知数のまま解の式に残す。

res = solve([eq2, eq3], (a, r1))

   1-element Vector{Tuple{Sym, Sym}}:
    (5*r2, 5*r2/3)

求まった解 a, r1 を既知として r3, y3 を求める。

@syms a::positive, r1::positive, r2::positive,
     r3::positive, y3::positive;

(a, r1) = (5*r2, 5*r2/3)
eq1 = (r1 - r3)^2 + y3^2 - (r1 + r3)^2
eq4 = (a - y3)*r1 - r3*a
solve([eq1, eq4], (r3, y3))

   1-element Vector{Tuple{Sym, Sym}}:
    (-10*r2*(-1/9 + sqrt(10)/9)/3 + 5*r2/3, 10*r2*(-1/9 + sqrt(10)/9))

天円の半径は r2 * 5(11 - 2*sqrt(10))/27 となり，小円の半径の 5(11 - 2*sqrt(10))/27 = 0.865823088826526 倍である。

-10*r2*(-1//9 + sqrt(Sym(10))//9)//3 + 5*r2//3 |> simplify |> println

   5*r2*(11 - 2*sqrt(10))/27

5(11 - 2*sqrt(10))/27

   0.865823088826526

小円の直径が 1 寸のとき，天円の直径は 0.865823088826526 = 8分6厘5毛8糸 有奇（あまりあり）。

   天円の直径 = 0.865823;  a = 2.5;  r1 = 0.833333;  r3= 0.432912;  y3= 1.20127

using Plots

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r2 = 1//2
   (a, r1) = (5*r2, 5*r2/3)
   (r3, y3) = (-10*r2*(-1/9 + sqrt(10)/9)/3 + 5*r2/3, 10*r2*(-1/9 + sqrt(10)/9))
   @printf("天円の直径 = %g;  a = %g;  r1 = %g;  r3= %g;  y3= %g\n", 2r3, a, r1, r3, y3)
   plot([a, a, -a, -a, a], [-a, a, a, -a, -a], color=:black, lw=0.5)
   circle42(0, a - r1, r1)
   circle4(a - r3, y3, r3, :blue)
   circle(0, 0, r2, :magenta)
   plot!([-a, 0, a], [a, 2r1 - a, a], color=:green, lw=0.5)
   plot!([-a, 0, a], [-a, a - 2r1, -a], color=:green, lw=0.5)
   x = r1*a/(a - 3)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /  3  # size[2] * fontsize * 2
       point(a - 2r1, 0, " a-2r1")
       point(0, a - 2r1, " a-2r1")
       point(0, a - r1, " 大円:r1\n (0,a-r1)", :red, :left, :vcenter)
       point(a - r1, 0, "r1", :red, :center, :bottom, delta=delta)
       point(a, 0, "a ", :red, :right, :bottom, delta=delta)
       point(0, 0, " 小円\n r2", :magenta, :left, :top, delta=-delta/2)
       point(0, r2, " r2", :magenta, :left, :top, delta=-delta)
       point(a - r3, y3, "天円:r3 \n(a-r3,y3) ", :blue, :right, :vcenter)
       
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
   end
end;

 

算額（その473）

算額（その473）

宮城県石巻市雄勝町 葉山神社 明治17年(1884)

徳竹亜紀子，谷垣美保: 2021年度の算額調査，仙台高等専門学校名取キャンパス 研究紀要，第 58 号, p.7-28, 2022.
https://www.sendai-nct.ac.jp/natori-library/wp/wp-content/uploads/2022/03/kiyo2022-2.pdf

外円の中に大円，中円，小円が 2 個ずつ入っている。小円の直径が 8 寸のとき，大円の直径を求めよ。

外円の半径と中心座標を r0, (0, 0); r0 = 2r1
大円の半径と中心座標を r1, (0, r1)
中円の半径と中心座標を r2, (r2, y2)
小円の半径と中心座標を r3, (x3, y3)
とおき，以下の連立方程式を解く。

include("julia-source.txt")

using SymPy
@syms r0::positive, r1::positive, r2::positive, y2::positive,
     r3::positive, x3::positive, y3::negative;

r0 = 2r1
eq1 = r2^2 + (y2 + r1)^2 - (r1 + r2)^2
eq2 = (x3 - r2)^2 + (y2 - y3)^2 - (r2 + r3)^2
eq3 = r2^2+ y2^2 - (r0 - r2)^2
eq4 = x3^2 + y3^2 - (r0 - r3)^2
eq5 = x3^2 + (r1 + y3)^2 - (r1 + r3)^2

res = solve([eq1, eq2, eq3, eq4, eq5], (r1, r2, y2, x3, y3))

   1-element Vector{NTuple{5, Sym}}:
    (17*r3/8, 17*r3/9, 17*r3/12, 3*r3, -5*r3/4)

大円の直径は小円の直径の 17/8 倍である。
小円の直径が 8 寸のとき，大円の直径は 17 寸である。

大円の直径 = 17;  r0 = 17;  r1 = 8.5;  r2= 7.55556;  y2= 5.66667;  r3 = 4;  x3= 12;  y3= -5

using Plots

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r3 = 8//2
   (r1, r2, y2, x3, y3) =  (17*r3/8, 17*r3/9, 17*r3/12, 3*r3, -5*r3/4)
   r0 = 2r1
   @printf("大円の直径 = %g;  r0 = %g;  r1 = %g;  r2= %g;  y2= %g;  r3 = %g;  x3= %g;  y3= %g\n",
       2r1, r0, r1, r2, y2, r3, x3, y3)
   plot()
   circle(0, 0, r0, :black)
   circle(0, r1, r1, :red)
   circle(0, -r1, r1, :red)
   circle(r2, y2, r2, :blue)
   circle(-r2, y2, r2, :blue)
   circle(x3, y3, r3, :green)
   circle(-x3, y3, r3, :green)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /  3  # size[2] * fontsize * 2
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
       point(0, r1, " 大円:r1,(0,r1)", :red, :left, :vcenter)
       point(r2, y2, "  中円:r2\n  (r2,y2)", :blue, :left, :vcenter)
       point(x3, y3, "小円:r3\n(x3,y3)", :green, :center, :top, delta=-delta)
       point(2r1, 0, "r0 ", :black, :right, :bottom, delta=delta/3)
   end
end;

算額（その472）

算額（その472）

宮城県角田市横倉 愛宕神社 明治15年(1882)1月
http://www.wasan.jp/miyagi/yokokuraatago.html

徳竹亜紀子，谷垣美保: 2021年度の算額調査，仙台高等専門学校名取キャンパス 研究紀要，第 58 号, p.7-28, 2022.
https://www.sendai-nct.ac.jp/natori-library/wp/wp-content/uploads/2022/03/kiyo2022-2.pdf

団扇の中に，正三角形，大円 2 個，小円 2 個が入っている。大円の直径が 23 寸 4 分のとき，小円の直径はいかほどか。

扇を構成する外円の半径と中心座標を r0, (0, 0)
大円の半径と中心座標を r1, (r1, r1 - r0/2)
小円の半径と中心座標を r2, (x2, -r2 - r0/2)
団扇の下部の円弧の半径と中心座標を r0/2, (0, -r0)
外円と円弧の交点座標を (x, y)
とおき，以下の連立方程式を解く。

include("julia-source.txt")

using SymPy
@syms r0::positive, r1::positive, r2::positive, x2::positive;
r1 = 234//20
eq1 = x2^2 + (r0/2 - r2)^2 - (r0/2 + r2)^2
eq2 = r1^2 + (r1 - r0/2)^2 - (r0 - r1)^2
eq3 = x2^2 + (-r0/2 - r2)^2 - (r0 - r2)^2
res = solve([eq1, eq2, eq3], (r0, r2, x2))

   1-element Vector{Tuple{Sym, Sym, Sym}}:
    (117/5, 351/100, 117*sqrt(30)/50)

外円の直径は大円の直径の 2 倍である（方程式によらなくてもわかることではあるが）。
小円の直径は大円の直径の 3/10 倍である。23.4*3/10 = 7.02 = 7寸0分2厘である。

術では「大円の直径を3倍して「1位ずらす」（10で割る）」ことで，7 寸としている（普通は 7 寸あまりありと記載される）。

図を描くために円弧の描き始めと描き終わりの角度を求めるために，外円と円弧の交点座標 (x, y) を求める。

using SymPy
@syms r0::positive, r1::positive, x, y;
r1 = 234//20
r0 = 117//5
eq11 = x^2 + y^2 - r0^2
eq12 = x^2 + (y + r0)^2 - (r0/2)^2
rs2 = solve([eq11, eq12], (x, y))

   2-element Vector{Tuple{Sym, Sym}}:
    (-117*sqrt(15)/40, -819/40)
    (117*sqrt(15)/40, -819/40)

using Plots

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r1 = 234//20
   (r0, r2, x2) = (2*r1, 3*r1/10, sqrt(30)*r1/5)
   @printf("小円の直径 = %g;  r0 = %g;  r1 = %g;  r2= %g;  x2= %g\n", 2r2, r0, r1, r2, x2)
   plot([√3r0/2, 0, -√3r0/2, √3r0/2], [-r0/2, r0, -r0/2, -r0/2], color=:black, lw=0.5)
   circle(0, 0, r0, :black)
   circle(r1, r1 - r0/2, r1, :red)
   circle(-r1, r1 - r0/2, r1, :red)
   circle(x2, -r2 - r0/2, r2, :blue)
   circle(-x2, -r2 - r0/2, r2, :blue)
   (x, y) = (117*sqrt(15)/40, -819/40)
   θ = round(Int, atand(Float64((y + r0)/x)))
   circle(0, -r0, r0/2, :green, beginangle=θ, endangle=180 - θ)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /  3  # size[2] * fontsize * 2
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
       point(r1, r1 - r0/2, "大円:r1,(r1,r1-r0/2)", :red, :center, :top, delta=-delta)
       point(x2, -r2 - r0/2, "小円:r2,(x2,-r2-r0/2)", :blue, :center, :top, delta=-delta)
       point(0, -r0/2, " -r0/2", :black, :left, :bottom, delta=delta/3)
       point(0, -r0, " -r0", :green, :left, :bottom, delta=delta/3)
       point(√3r0/2, -r0/2, "(√3r0/2,-r0/2) ", :black, :right, :bottom, delta=delta/3)
       point(x, y, "(x,y)")
   end
end;

算額（その471）

算額（その471）

宮城県角田市横倉 愛宕神社 明治15年(1882)1月
http://www.wasan.jp/miyagi/yokokuraatago.html

徳竹亜紀子，谷垣美保: 2021年度の算額調査，仙台高等専門学校名取キャンパス 研究紀要，第 58 号, p.7-28, 2022.
https://www.sendai-nct.ac.jp/natori-library/wp/wp-content/uploads/2022/03/kiyo2022-2.pdf

二等辺三角形（圭）内に全円と菱形，および等円 2 個が入っている。全円の直径が 14 寸のとき，等円の直径を求めよ。

二等辺三角形の底辺の長さを 2a, 高さを b とする。また，菱形の右端の頂点座標を(c, r1) とする。
全円の半径と中心座標を r1，(0, r1)
等円の半径と中心座標を r2, (x2, 0)
とし，以下の連立方程式を解く。

include("julia-source.txt")

using SymPy
@syms a::positive, b::positive, c::positive,
     r1::positive, r2::positive, x2::positive;
r1 = 14//2
eq1 = x2^2 + (r1 - r2)^2 - (r1 + r2)^2
eq2 = (a - x2)r1 - r2*a
eq3 = (b - r1)a - b*c
eq4 = ((b - r1)a/r1)^2 - (b^2 + a^2)
eq5 = r1/(a - c) - b/a
eq5 = r1*a - (a - c)b
#eq5 = (2a +2sqrt(a^2 + b^2))r1/2 - a*b
#eq5 = distance(a, 0, 0, b, x2, r2) - r2^2
res = solve([eq1, eq2, eq3, eq4], (a, c, r2, x2))

   2-element Vector{NTuple{4, Sym}}:
    (sqrt(3*b - 2*sqrt(2)*sqrt(b^2 - 21*b + 98) - 28)*(7*b + 7*sqrt(2*b^2 - 42*b + 196) - 98)/(sqrt(b)*(b - 14)), sqrt(3*b - 2*sqrt(2)*sqrt(b^2 - 21*b + 98) - 28)*(7*b^2 + 7*b*sqrt(2*b^2 - 42*b + 196) - 147*b - 49*sqrt(2*b^2 - 42*b + 196) + 686)/(b^(3/2)*(b - 14)), (21*b - 14*sqrt(2*b^2 - 42*b + 196) - 196)/b, sqrt(588*b - 392*sqrt(2)*sqrt(b^2 - 21*b + 98) - 5488)/sqrt(b))
    (sqrt(3*b + 2*sqrt(2)*sqrt(b^2 - 21*b + 98) - 28)*(7*b - 7*sqrt(2*b^2 - 42*b + 196) - 98)/(sqrt(b)*(b - 14)), sqrt(3*b + 2*sqrt(2)*sqrt(b^2 - 21*b + 98) - 28)*(7*b^2 - 7*b*sqrt(2*b^2 - 42*b + 196) - 147*b + 49*sqrt(2*b^2 - 42*b + 196) + 686)/(b^(3/2)*(b - 14)), (21*b + 14*sqrt(2*b^2 - 42*b + 196) - 196)/b, sqrt(588*b + 392*sqrt(2)*sqrt(b^2 - 21*b + 98) - 5488)/sqrt(b))

2 組の解が得られるが，最初のものが適解である。しかし，解はすべて b が含まれている。つまり，b は任意の値を取りうるということである。

問の中の条件として「全円の直径が 14 寸のとき」とあるだけで b に関する条件がない。
図において，二等辺三角形の斜辺は全円の接線になるので，b が小さくなれば a は大きくなり，それに連れて等円の半径も大きくなる。「逆も真なり」である。

res[1][3] |> println

   (21*b - 14*sqrt(2*b^2 - 42*b + 196) - 196)/b

術では，「等円の直径は，全円の直径を 2 倍して 7 で割る」としている。等円の半径が 2 になるときの b は 784/31 = 25.2903225806452 である。

solve(res[1][3] - 2)[1].evalf() |> println

   25.2903225806452

res[1][3](b => 784/31) |> println

   2.00000000000000

等円の直径 = 4;  a = 10.4766;  b = 25.2903;  c = 7.57686;  r2= 2;  x2= 7.48331

たとえば b = 17 のときは，等円の直径は 7 になる。
等円の直径 = 7;  a = 19.799;  b = 16;  c = 11.1369;  r2= 3.5;  x2= 9.89949
これを術もどきでいうと「等円の直径は，全円の直径を 2 倍して 4 で割る」ことになってしまう。

using Plots

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r1 = 14//2
   b = 784/31  # 25.2903225806452
   (a, c, r2, x2) = (sqrt(3*b - 2*sqrt(2)*sqrt(b^2 - 21*b + 98) - 28)*(7*b + 7*sqrt(2*b^2 - 42*b + 196) - 98)/(sqrt(b)*(b - 14)), sqrt(3*b - 2*sqrt(2)*sqrt(b^2 - 21*b + 98) - 28)*(7*b^2 + 7*b*sqrt(2*b^2 - 42*b + 196) - 147*b - 49*sqrt(2*b^2 - 42*b + 196) + 686)/(b^(3/2)*(b - 14)), (21*b - 14*sqrt(2*b^2 - 42*b + 196) - 196)/b, sqrt(588*b - 392*sqrt(2)*sqrt(b^2 - 21*b + 98) - 5488)/sqrt(b))
   @printf("等円の直径 = %g;  a = %g;  b = %g;  c = %g;  r2= %g;  x2= %g\n", 2r2, a, b, c, r2, x2)
   plot([a, 0, -a, 0], [0, b, 0, 0], color=:black, lw=0.5)
   plot!([c, 0, -c, 0, c], [r1, 2r1, r1, 0, r1], color=:blue, lw=0.5)
   circle(0, r1, r1, :red)
   circle(x2, r2, r2, :magenta)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /  3  # size[2] * fontsize * 2
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
       point(a, 0, "a", :black, :left, :bottom, delta=delta/2)
       point(0, b, " b", :black, :left, :vcenter)
       point(c, r1, " (c,r1)", :blue, :left, :vcenter)
       point(0, r1, " 全円:r1,(0,r1)", :red, :left, :vcenter)
       point(x2, r2, "等円:r2,(x2,r2)", :magenta, :center, :top, delta=-delta)
       point(0, 2r1, " 2r1", :red, :left, :bottom, delta=delta/2)
       
   end
end;

算額（その470）

算額（その470）

宮城県角田市横倉 愛宕神社 明治15年(1882)1月
http://www.wasan.jp/miyagi/yokokuraatago.html

徳竹亜紀子，谷垣美保: 2021年度の算額調査，仙台高等専門学校名取キャンパス 研究紀要，第 58 号, p.7-28, 2022.
https://www.sendai-nct.ac.jp/natori-library/wp/wp-content/uploads/2022/03/kiyo2022-2.pdf

甲円内に弦を挟んで乙円 1 個，丙円 1 個，丁円 2 個が入っている。
乙円，丙円，丁円の直径がそれぞれ 4 寸，3 寸，1 寸のとき，甲円の直径を求めよ。

甲円の半径と中心座標を r1, (0, 0)
乙円の半径と中心座標を r2, (x2, 2r4 - r1 + r2)
丙円の半径と中心座標を r3, (x3, 2r4 - r1 + r3)
丁円の半径と中心座標を r4, (0, r4 - r1), (x4, 3r4 - r1)
とし，以下のように記号を定め方程式を解く。

include("julia-source.txt")

using SymPy
@syms r1::positive, r2::positive, x2::positive,
     r3::positive, x3::negative,
     r4::positive, x4::negative;
eq1 = x2^2 + (2r4 - r1 + r2)^2 - (r1 - r2)^2
eq2 = x3^2 + (2r4 - r1 + r3)^2 - (r1 - r3)^2
eq3 = (x2 - x4)^2 + (r2 - r4)^2 - (r2 + r4)^2
eq4 = (x3 - x4)^2 + (r3 - r4)^2 - (r3 + r4)^2
solve([eq1, eq2, eq3, eq4], (r1, x2, x3, x4))

   2-element Vector{NTuple{4, Sym}}:
    (r2 + r3 + r4, 2*sqrt(r4)*(-sqrt(r2)*sqrt(r3) + r3)*sqrt(2*sqrt(r2)*sqrt(r3) + r2 + r3)/(r2 - r3), 2*sqrt(r4)*(sqrt(r2)*sqrt(r3) - r2)*sqrt(2*sqrt(r2)*sqrt(r3) + r2 + r3)/(r2 - r3), -2*sqrt(r4)*sqrt(2*sqrt(r2)*sqrt(r3) + r2 + r3))
    (r2 + r3 + r4, 2*sqrt(r4)*(sqrt(r2)*sqrt(r3) + r3)*sqrt(-2*sqrt(r2)*sqrt(r3) + r2 + r3)/(r2 - r3), -2*sqrt(r4)*(sqrt(r2)*sqrt(r3) + r2)*sqrt(-2*sqrt(r2)*sqrt(r3) + r2 + r3)/(r2 - r3), -2*sqrt(r4)*sqrt(-2*sqrt(r2)*sqrt(r3) + r2 + r3))

2 組の解が得られるが，2 組目のものが適解である。

   r1 = 4;  x2 = 1.73205;  x3 = -2;  x4= -0.267949
   甲円の直径 = 8

甲円の半径は r2 + r3 + r4 すなわち，乙円，丙円，丁円の半径の和である。
乙円，丙円，丁円の直径がそれぞれ 4 寸，3 寸，1 寸ならば，甲円の直径は 4 + 3 + 1 = 8 寸である。

using Plots

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r2, r3, r4) = (4, 3, 1) .// 2
   (r1, x2, x3, x4) = (r2 + r3 + r4, 2*sqrt(r4)*(sqrt(r2)*sqrt(r3) + r3)*sqrt(-2*sqrt(r2)*sqrt(r3) + r2 + r3)/(r2 - r3), -2*sqrt(r4)*(sqrt(r2)*sqrt(r3) + r2)*sqrt(-2*sqrt(r2)*sqrt(r3) + r2 + r3)/(r2 - r3), -2*sqrt(r4)*sqrt(-2*sqrt(r2)*sqrt(r3) + r2 + r3))
   @printf("r1 = %g;  x2 = %g;  x3 = %g;  x4= %g\n", r1, x2, x3, x4)
   @printf("甲円の直径 = %g\n", 2r1)
   plot()
   circle(0, 0, r1, :red)
   circle(x2, 2r4 - r1 + r2, r2, :magenta)
   circle(x3, 2r4 - r1 + r3, r3, :blue)
   circle(x4, 3r4 - r1, r4, :green)
   circle(0, r4 - r1, r4, :green)
   segment(-sqrt(r1^2 - (2r4 - r1)^2), 2r4 - r1, sqrt(r1^2 - (2r4 - r1)^2), 2r4 - r1)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /  3  # size[2] * fontsize * 2
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
       point(0, r1, " r1", :red, :left, :bottom, delta=delta/2)
       point(x2, 2r4 - r1 + r2, "乙円:r2,(x2,2r4-r1+r2)", :magenta, :center, :top, delta=-delta)
       point(x3, 2r4 - r1 + r3, "丙円:r3,(x3,2r4-r1+r3)", :blue, :center, :top, delta=-delta)
       point(0, r4 - r1, " 丁円:r4\n (0,r4-r1)", :black, :left, :vcenter)
       point(x4, 3r4 - r1, "丁円:r4,(x4,3r4-r1) ", :black, :right, :vcenter)
       point(0.2r1, 0.5r1, " 甲円:r1,(0,0)", :red, :left, :vcenter)
       point(0, 2r4 - r1, " 2r4-r1", :black, :left, :bottom, delta=delta)
   end
end;

 

算額（その469）

算額（その469）

宮城県石巻市雄勝町 葉山神社 明治17年(1884)

徳竹亜紀子，谷垣美保: 2021年度の算額調査，仙台高等専門学校名取キャンパス 研究紀要，第 58 号, p.7-28, 2022.
https://www.sendai-nct.ac.jp/natori-library/wp/wp-content/uploads/2022/03/kiyo2022-2.pdf

半円内に等円が 4 個入っている。黒い部分の面積（黒積）はいかほどか。

include("julia-source.txt")

using SymPy

@syms r0::positive, r::positive, x1::negative, x2::positive,
     x3::negative, y3::positive;
@syms r0::positive, r::positive, x1::negative, x2::positive, x3::negative, y3::positive
eq1 = x1^2 + r^2 - (r0 - r)^2
eq2 = (x1 - x3)^2 + (y3 - r)^2 - 4r^2
eq3 = x3^2 + y3^2 - (r0 - r)^2
eq4 = (x2 + 2r)^2 + r^2 - (r0 - r)^2
eq5 = x1 + x2 - 2x3

res = solve([eq1, eq2, eq3, eq4, eq5], (r0, x1, x2, x3, y3))

   2-element Vector{NTuple{5, Sym}}:
    (r + sqrt(2)*r*sqrt(sqrt(2) + 2), -r*(1 + sqrt(2)), r*(-1 + sqrt(2)), -r, r + sqrt(2)*r)
    (-sqrt(2)*r*sqrt(sqrt(2) + 2) + r, -r*(1 + sqrt(2)), r*(-1 + sqrt(2)), -r, r + sqrt(2)*r)

2 組の解が求まるが，最初のものが適解である。

res[1]

   (r + sqrt(2)*r*sqrt(sqrt(2) + 2), -r*(1 + sqrt(2)), r*(-1 + sqrt(2)), -r, r + sqrt(2)*r)

等円の半径が 1/2 のとき，
r0 = 1.80656;  x1 = -1.20711;  x2 = 0.207107  x3 = -0.5;  y3 = 1.20711
である。

黒積は以下のようにして求めることができる。

扇形 OAB の面積は半径 r0 の円の 1/4 なので，π*r0^2/4 = π*r*(1 + sqrt(2√2 + 4))/4

@syms r

r0 = r*(1 + sqrt(2√Sym(2) + 4))
gray = PI*r0^2/4;

水色の三角形2個の面積は (2r*r/2)*2 = 2r^2

cyan = 2r^2;

赤い扇形の中心角は 157.5 度で，2 つ分の面積は (πr^2 * 157.5/360)*2 = π*r^2*(7/8)

red = PI*r^2*(7//8);

黄色い扇形の中心角は 135 度で，面積は πr^2*135/360 = π*r^2*(3/8)

yellow = PI*r^2*(3//8);

灰色の部分の面積は gray - cyan - red - yellow

S = gray - cyan - red - yellow;
S |> expand |> simplify

   r^2*(-2 + sqrt(2)*pi/2 + pi*sqrt(2*sqrt(2) + 4)/2)

等円の半径 r = 1/2 とすると，黒積は 1.08153252024683 である。

@syms r
S(r => 1/2).evalf() |> println

   1.08153252024683

術では
sqrt(1/2) を「位」とおけば，
((sqrt(位 + 1) + 位)*PI/4 - 1/2)^(2r)^2 で黒積が求められる。

位 = sqrt(1/2)
円積率 = pi/4
等円の直径 = 1
((sqrt(位 + 1) + 位)*円積率 - 1/2)*等円の直径^2

   1.0815325202468267

using Plots

function circlef2(ox, oy, r, color=:red; beginangle=0, endangle=360, by=0.5, n=0, alpha=0.4)
   n != 0 && (by = (endangle - beginangle) / n)
   θ = beginangle:by:endangle
   x = r.*cosd.(θ)
   y = r.*sind.(θ)
   append!(x, [0, x[1]])
   append!(y, [0, y[1]])
   plot!(ox .+ x, oy .+ y, linecolor=:black, linewidth=0.5, seriestype=:shape, fillcolor=color, alpha=alpha)
end;

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r = 1/2
   (r0, x1, x2, x3, y3) = (
       r*(1 + sqrt(2√2 + 4)),
       r*(-√2 - 1),
       r*(√2 - 1),
       -r,
       r*(1 + √2))
   @printf("r0 = %g;  x1 = %g;  x2 = %g  x3 = %g;  y3 = %g\n", r0, x1, x2, x3, y3)
   plot()
   circle(0, 0, r0, :blue, beginangle=0, endangle=180)
   circlef2(0, 0, r0, :black, beginangle=22.5, endangle=112.5)
   circle(x1, r, r)
   circle(x2, r, r)
   circlef2(x2, r, r, :orange, beginangle=0, endangle=135, alpha=0.8)
   circle(x2 + 2r, r, r)
   circlef2(x2 + 2r, r, r, beginangle=22.5, endangle=180, alpha=0.8)
   circle(x3, y3, r)
   circlef2(x3, y3, r, beginangle=-45, endangle=112.5, alpha=0.8)
   segment(0, 0, r0*x3/sqrt(x3^2 + y3^2), r0*y3/sqrt(x3^2 + y3^2))
   segment(0, 0, r0*y3/sqrt(x3^2 + y3^2), -r0*x3/sqrt(x3^2 + y3^2))
   segment(x2, r, x3, y3)
   segment(x2, r, x2 + 2r, r)
   segment(0, 0, x2, r)
   plot!([0, x2 + 2r, x2, 0], [0, r, r, 0], linewidth=0.5, seriestype=:shape, fillcolor=:cyan, alpha=0.8)
   plot!([0, x2, x3, 0], [0, r, y3, 0], linewidth=0.5, seriestype=:shape, fillcolor=:cyan, alpha=0.8)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /  3  # size[2] * fontsize * 2
       hline!([0], color=:gray, lw=0.5)
       vline!([0], color=:gray, lw=0.5)
       plot!(ylims=(-0.1r0, r0))
       point(r0*x3/sqrt(x3^2 + y3^2), r0*y3/sqrt(x3^2 + y3^2), "A", :blue, :right, :bottom, delta=delta)
       point(r0*y3/sqrt(x3^2 + y3^2), -r0*x3/sqrt(x3^2 + y3^2), " B", :blue, :left, :vcenter)
       point(0, 0, "O ", :blue, :right, :top, delta=-delta)
       point(x1, r, "(x1,r)", :red)
       point(x2, r, "(x2,r)", :white, :left, :bottom, delta=delta)
       point(x2 + 2r, r, "(x2+2r,r)", :white, :right, :bottom, delta=delta)
       point(x3, y3, " (x3,y3)", :white, :left, :vcenter)
   else
      plot!(showaxis=false)
   end
end;

 

算額（その468）

算額（その468）

泉州堺大寺三村明神社 文政8年
関流 林助右衛門自弘門人
泉州堺 岸喜八郎忠義

安藤洋美: 泉州の算額，桃山学院大学総合研究所紀要，第 24 巻，第 3 号，p.119-144.
https://www.andrew.ac.jp/soken/assets/wr/sokenk104_4.pdf

長方形の中に楕円と正方形と円が入っている。長方形の長辺，短辺が与えられたとき，正方形の一変の長さと円の直径を求めよ。

楕円の長径，短径を a，c，長方形の長辺，短辺をそれぞれ 2b, 2a，楕円の長径円の半径を r とする。
正方形の左の頂点の座標を (x, y) とする。
長方形内の「四辺形」が正方形であるためには x = b - a でなければならない。
以上を踏まえて連立方程式を立て解を求める。なおそれぞれの方程式は独立なので，eq1, eq2, eq3 を順次解くこともできる（x, y, r それぞれの数式解を求めることもできる）。

include("julia-source.txt")

using SymPy

@syms a::positive, b::positive, c::positive, h::positive,
     k::positive, m::positive, x::positive, y::positive,
     r::positive;

(a, b, c) = (5, 7.5, 3)
eq1 = x^2/c^2 + y^2/a^2 - 1
eq2 = distance(x, y, b - y, 0, c + r, 0) - r^2
eq3 = b - x - a

res = solve([eq1, eq2, eq3], (x, y, r))

   1-element Vector{Tuple{Sym, Sym, Sym}}:
    (2.50000000000000, 2.76385399196283, 0.759366262899728)

   x = 2.5;  y = 2.76385;  r = 0.759366
   正方形の一辺の長さ = 3.55517

using Plots

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (a, b, c) = (5, 7.5, 3)
   (x, y, r) = res[1]
   @printf("x = %g;  y = %g;  r = %g\n", x, y, r)
   @printf("正方形の一辺の長さ = %g\n", sqrt(y^2 + (a - y)^2))
   plot([b, b, -b, -b, b], [-a, a, a, -a, -a], color=:black, lw=0.5)
   ellipse(0, 0, c, a, color=:green)
   plot!([b - y, b, x + y, x, b - y], [0, a - y, a, y, 0], color=:blue, lw=0.5)
   plot!([y - b, -b, -x - y, -x, y - b], [0, a - y, a, y, 0], color=:blue, lw=0.5)
   plot!([b - y, b, x + y, x, b - y], [0, y - a, -a, -y, 0], color=:blue, lw=0.5)
   plot!([y - b, -b, -x - y, -x, y - b], [0, y - a, -a, -y, 0], color=:blue, lw=0.5)
   circle(c + r, 0, r)
   circle(-c - r, 0, r)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /  3  # size[2] * fontsize * 2
       hline!([0], color=:gray, lw=0.5)
       vline!([0], color=:gray, lw=0.5)
       point(x, y, " (x, y)", :green, :left, :vcenter)
       point(b - y, 0, "   b-y", :blue, :left, delta=-delta/2)
       point(c, 0, " c ", :green, :right, delta=-delta/2)
       point(c + r, 0, " c+r", :red, :center, delta=-delta/2)
       point(b, 0, "b ", :black, :right, :bottom, delta=delta/2)
       point(0, a, " a", :black, :left, :bottom, delta=delta/2)
   else
      plot!(showaxis=false)
   end
end;

 

算額（その467）

算額（その467）

泉州堺大寺三村明神社 文政8年
関流 林助右衛門自弘門人
泉州堺 岸喜八郎忠義

安藤洋美: 泉州の算額，桃山学院大学総合研究所紀要，第 24 巻，第 3 号，p.119-144，1999.
https://www.andrew.ac.jp/soken/assets/wr/sokenk104_4.pdf

大円と小円が交わった中に甲円，乙円，丙円が入っている。大円，小円の直径がそれぞれ 56 寸，42 寸のとき，丙円の直径を求めよ。

安藤は「丙円が最大になるのは大円と小円の交点の x 座標が 0 になるとき（大円の中心座標の x 座標は 7√7）である。そして，丙円の直径の最大値は 15.216699593485583 寸になる。」としているが，それは間違いである（仮定が間違っている）。
丙円の直径の最大値は 15.256396062995767 寸になる。

小円の中心を原点とする。
大円の半径と中心座標を r1, (x1, 0)
小円の半径と中心座標を r2, (0, 0)
甲円の半径と中心座標を r3, (x3, 0); x3 = r2 - r3 - 2r4
乙円の半径と中心座標を r4, (x4, 0); x4 = r2 - r4
丙円の半径と中心座標を r5, (x5, y5)
とおき，以下の連立方程式を解く。
r3, r4, r5, x5, y5 は x1, r1, r2 を含む式になる。
r1, r2 は事前に与えられているが，任意の値を代入できる。

include("julia-source.txt")

using SymPy

@syms r1, r2, r3, r4, x1, r5, x5, y5;

x3 = r2 - r3 - 2r4
x4 = r2 - r4
eq1 = (x1 - x5)^2 + y5^2 - (r1 - r5)^2
eq2 = x5^2 + y5^2 - (r2 - r5)^2
eq3 = (x3 - x5)^2 + y5^2 - (r3 + r5)^2
eq4 = (x4 - x5)^2 + y5^2 - (r4 + r5)^2
eq5 = (2r3 + 2r4) - (r1 - x1  + r2)
res = solve([eq1, eq2, eq3, eq4, eq5], (r3, r4, r5, x5, y5));

4 組の解が求まるが，2 番目のものが適解である。

res[2][3](r1 => 28, r2 => 21) |> println

   (x1^6 - 98*x1^5 + 2303*x1^4 + 9604*x1^3 + 8*sqrt(7)*x1^2*sqrt(21*x1^6 - 3087*x1^4 + 151263*x1^2 - 2470629) - 232897*x1^2 - 392*sqrt(7)*x1*sqrt(21*x1^6 - 3087*x1^4 + 151263*x1^2 - 2470629) - 235298*x1 + 5764801)/(2*(x1^5 - 147*x1^4 + 98*x1^3 + 4802*x1^2 - 7203*x1 + 117649))

r = res[2][3](r1 => 28, r2 => 21)
pyplot(size=(400, 300), grid=false, aspectratio=:none, label="", fontfamily="IPAMincho")
plot(r, xlims=(16.8, 19))
vline!([17.1249692175712 7√7], color=[:blue :red], lw=0.5)
point(17.1249692175712, 7.61, " x1 = 17.1249692175712", :blue, :left, mark=false)
point(7√7, 7.6, "x1 = 7√7 ", :red, :right, mark=false)

r が最大になる x1(=17.1249692175712) を求めるのは以下のようにする。
導関数を求め，導関数が 0 になる（接線の傾きが 0 になる）ときの x1 を求める。

res2 = solve(diff(r)) |> N

   2-element Vector{BigFloat}:
     17.12496921757124267110541465838727820166138780094414631498498630254248473183871
    283.6412388251531475102078272011544864078032045775545462752953962935519173703001

2 つの解が求まるが，最初のものが適解である。

r の式の x1 に 17.1249692175712 を代入して 2 倍すれば，丙円の直径になる。

2r(x1 => 17.1249692175712) |> N

   15.25639606299576571629052483808411446102625164217199486538658100674758025392085

r の導関数の x1 に 17.1249692175712 を代入すると 0 になっている。

diff(r)(x1 => 17.1249692175712) |> N

   1.181732923487665208021280584871855071474434670510598437485481357938685752092638e-15

println("r3 = ", res[2][1](r1 => 28, r2 => 21, x1 => 17.1249692175712).evalf())
println("r4 = ", res[2][2](r1 => 28, r2 => 21, x1 => 17.1249692175712).evalf())
println("r5 = ", res[2][3](r1 => 28, r2 => 21, x1 => 17.1249692175712).evalf())
println("x5 = ", res[2][4](r1 => 28, r2 => 21, x1 => 17.1249692175712).evalf())
println("y5 = ", res[2][5](r1 => 28, r2 => 21, x1 => 17.1249692175712).evalf())

   r3 = 6.82022432957484
   r4 = 9.11729106163957
   r5 = 7.62819803149788
   x5 = 1.66596921777779
   y5 = 13.2676160047785

using Plots

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r1, r2) = (56, 42) .// 2
   x1 = 17.1249692175712
   r3 = 6.82022432957484
   r4 = 9.11729106163957
   r5 = 7.62819803149788
   x5 = 1.66596921777779
   y5 = 13.2676160047785
   x3 = r2 - r3 - 2r4
   x4 = r2 - r4
   @printf("r3 = %g;  r4 = %g;  r5 = %g;  x5 = %g;  y5 = %g\n", r3, r4, r5, x5, y5)
   @printf("丙円の直径は %g である。\n", 2r5)
   plot()
   circle(x1, 0, r1, :blue)
   circle(0, 0, r2, :red)
   circle(x3, 0, r3, :pink)
   circle(x4, 0, r4, :brown)
   circle(x5, y5, r5, :orange)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /  3  # size[2] * fontsize * 2
       hline!([0], color=:gray, lw=0.5)
       vline!([0], color=:gray, lw=0.5)
       point(x1, 0, "x1", :blue, :center, :top, delta=-delta)
       point(x1 - r1, 0, "x1-r1 ", :blue, :right)
       point(r2, 0, " r2", :red, :left, :bottom, delta=delta)
       point(x5, y5, "丙円:r5\n(x5,y5)", :orange, :center, :bottom, delta=delta)
       point(x3, 0, "甲円:r3\n(r2-r3-2r4,0)", :black, :center, delta=-2delta)
       point(x4, 0, "乙円:r4\n(r2-r4,0)", :brown, :center, :bottom, delta=delta)
   else
      plot!(showaxis=false)
   end
end;