算額(その1640)
九 岩手県奥州市(旧水沢市佐倉河) 胆沢城 八幡宮 弘化2年(1845)
山村善夫:現存 岩手の算額,昭和52年1月30日,熊谷印刷,盛岡市.
http://www.wasan.jp/yamamura/yamamura.html
今有如図 03076
https://w.atwiki.jp/sangaku/pages/137.html
一関博物館 和算に挑戦 令和5年度出題問題(3)[上級問題](高校生・一般向き)
https://www.city.ichinoseki.iwate.jp/museum/wasan/r5/hard.html
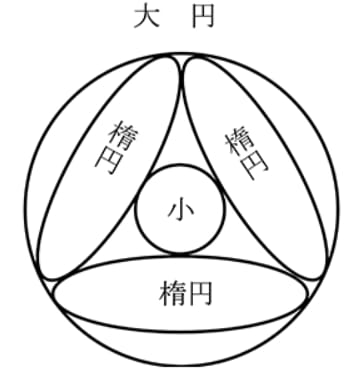
大円の中に楕円 3 個と小円を容れる。楕円の面積が最大になるとき,大円の直径を小円の直径で表す術を述べよ。
この算額は「算額(その678)」と求めるものが違うだけで,本質的に同じ問題である。

変数値が正の値を取るように,上下を反転させて解く。
大円の半径と中心座標を R, (0, 0)
小円の半径と中心座標を r, (0, 0)
楕円の超半径,短半径,中心座標を a, b, (0, y)
楕円と円の接点座標を (x1, y1)
楕円同士の接点座標を (x2, y2)
とおき,以下の連立方程式を解く。
include("julia-source.txt");
# julia-source.txt ソース https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf
using SymPy
@syms x1::positive, y1::positive, x2::positive, y2::positive, y::positive, a::positive, b::positive, R::positive
y2 = x2/sqrt(Sym(3))
eq1 = x1^2/a^2 + (y1 - y)^2/b^2 - 1
eq2 = b^2*x1/(a^2*(y - y1)) + x1/y1
eq3 = x1^2 + y1^2 - R^2
eq4 = x2^2/a^2 + (y2 - y)^2/b^2 - 1
eq5 = b^2*x2/(a^2*(y - y2))- 1/sqrt(Sym(3));
eq1, eq2, eq3 を解き,x1, y1, y を求める。
res1 = solve([eq1, eq2, eq3], (x1, y1, y))[1] # 1 of 2
(sqrt((-R^2*b^2 + a^4)/(a - b))/sqrt(a + b), a*sqrt(R^2*a^2 - R^2*b^2 - a^4 + a^2*b^2)/(a^2 - b^2), sqrt(R^2*a^2 - R^2*b^2 - a^4 + a^2*b^2)/a)
eq4, eq5 を解き,x2, y を求める。
res2 = solve([eq4, eq5], (x2, y))[1]
(a^2/sqrt(a^2 + 3*b^2), sqrt(3*a^2 + 9*b^2)/3)
res1 と res2 の y は等しいので,次の法定式を立てる。
eq = res1[3] - res2[2]
eq |> println
-sqrt(3*a^2 + 9*b^2)/3 + sqrt(R^2*a^2 - R^2*b^2 - a^4 + a^2*b^2)/a
b を求める。
ans_b = solve(eq, b)[1]
ans_b |> println
a*sqrt(9*R^2 - 12*a^2)/(3*R)
楕円の面積 S は πab である。
S = PI * a * ans_b;
面積が最大になるときの長半径を求めるには,S(a) の導関数 S(a)'を求め,S(a)'= 0 を解く。
max_at_a = solve(diff(S, a), a)[1]
max_at_a |> println
sqrt(2)*R/2
楕円の面積が最大になるときの長半径は √2R/2,
ans_b = ans_b(a => max_at_a)
ans_b |> println
sqrt(6)*R/6
同じく短半径は √6R/6
ans_y = res2[2](b =>ans_b)(a => max_at_a)
ans_y |> println
sqrt(3)*R/3
そのときの,中心座標の y 座標値は √3R/3 である。
小円の半径は r = ans_y - ans_b = (√3/3 - √6/6)*R で,
R = r/(√3/3 - √6/6) = r*(√6 + 2√3) すなわち,大円の直径は小円の直径の (√6 + 2√3) = 5.913591357920932 倍である。
@syms r, d
apart(r / (√Sym(3)/3 - √Sym(6)/6), d) |> simplify |> factor |> println
r*(sqrt(6) + 2*sqrt(3))
山村も「今有如図」も,術は √(√285 + 28) となっている。山村も「今有如図」も誤記(誤読)には気づいていない(問題を実際に解いていないのであろう)。
一関博物館のページでは,「術では √(√288 + 18) となっている」としている。二重根号を外せば √(√288 + 18) = √6 + 2√3 である。
√(√Sym(288) + 18) |> sympy.sqrtdenest |> println
sqrt(6) + 2*sqrt(3)
function draw(r, more)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
R = r*(√6 + 2√3)
a = √2R/2
b = √6R/6
y = √3R/3
x1 = sqrt((-R^2*b^2 + a^4)/(a - b))/sqrt(a + b)
y1 = a*sqrt(R^2*a^2 - R^2*b^2 - a^4 + a^2*b^2)/(a^2 - b^2)
x2 = a^2/sqrt(a^2 + 3*b^2)
y2 = y2 = √3x2/3
println((x1, y1))
println((x2, y2))
plot()
circle(0, 0, R)
circle(0, 0, r, :green)
ellipse(0, y, a, b, color=:blue)
ellipse(y*cosd(30), -y*sind(30), a, b, color=:blue, φ=-120)
ellipse(-y*cosd(30), -y*sind(30), a, b, color=:blue, φ=120)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(x1, y1, "(x1,y1)", :green, :left, :bottom, delta=delta/2)
point(x2, y2, "(x2,y2)", :green, :left, delta=-delta/2)
point(0, R, "R", :red, :center, :bottom, delta=delta/2)
point(0, r, "r", :green, :center, :bottom, delta=delta/2)
point(0, y, " y=r+b", :green, :center, :bottom, delta=delta/2)
end
end;
draw(1/2, true)