Part0アサルトキャノン予定立てとか。
Part1アサルトキャノンのもろもろ性質とか。
Part1.5アサルトキャノン射程について。
Part2アサルトキャノン攻撃力のPA依存性について。
Part3アサルトキャノン攻撃力のAA攻撃力/OB依存性について。
Part3.01レギュ変化に伴い心機一転
Part4PA16000~19555でのアサルトキャノン攻撃力
Part5PA12000~16000でのアサルトキャノン攻撃力
Part5.5Part4,5における計算式の改変
Part6PA9000~12000でのアサルトキャノン攻撃力
Part7PA9000以下のアサルトキャノン攻撃力とまとめ
今回はPA12000~16000でのアサルトキャノン攻撃力(レギュ1.20)について。
測定条件は、アサルトキャノン発動側のPAが12000、13000、14000、15000になったぐらいで他は前回と一緒。PA16000部分は細部が異なる2種類の攻撃力計算式の切り替わりポイントのため、前回の数値を流用する。
まず実測値↓

特定PA、特定AA攻撃力/OBでの攻撃力。実はPA14000以下ぐらいから計算式のめぼしがついてきたため、計測基準が微妙に変化していたりします。PA16000、15000と14000の途中ぐらいまでは数回計測した最大値を使用、それ以外では最大値を使用していたり計算値に極めて近い値が出たらそれを使用していたりPA12000ではまた頑張って最大値を求めたりと割と適当だったり。その基準の変化が結果に及ぼす影響とかあるでしょうが、今回はそんなものよりも、私自身の解釈による比重が非常に大きいですのでよろしく。
グラフは、

表に記載されている「傾き」、「切片」というのは、↑のグラフの近似直線の傾きと切片を指します。
グラフ見るとわかりますが、整波性能を1000とか上げるよりも、OBをAA攻撃力の高いものに換えた方が攻撃力変化が大きいです。ただ、AA攻撃力4600以上はP-MARROWを装備する必要があるため、実現が容易かと言われるとそうでもない。
切片部分について、グラフとその近似式は、

PA16000~19555の前回では、切片の式は、0.25×(PA-4000)+963 (963:レギュ1.20現在のLETHALDOSEに設定されたアサルトキャノン攻撃力) と予測しました。今回もそれと同様の式と考えられ、良い近似を示します。最大値とか多く使っているため2とか3ぐらい過大評価されていても気にしない。個人的にはグラフから判断するなら966にしたいんだけれど表示スペックを尊重。
傾きについてですが、ここからゴリ押しなのでやばいです。普通に近似式を求めると、
傾きの近似式
=0.000241568×整波性能+8.635787284 R^2=0.999999271

前回、乱数を考慮しない状態で、
アサルトキャノン攻撃力=12.5×AA攻撃力/OB+0.25×(PA-4000)+963(PA16000~19555)
と求めました。これの精度については今更どうこう言いませんが、ここから束縛条件として、PA16000のとき
(傾き-傾き)×PA整波性能(16000)+(傾き-切片)=12.5…A
であると言えます。
傾きの値に着目すると、
11.5349747
↓
11.77595731
↓
12.01732009
↓
12.25932791
↓
12.5011304(12.5)
PAが1000増えるごとに、0.25よりは少ない変化量…ただし0.24よりは気持ち大きい変化量であることが分かります。
候補その1…傾き-傾き=0.000241、傾き-切片=8.644、これはAを満たす。
切片を8.644に補正する場合、
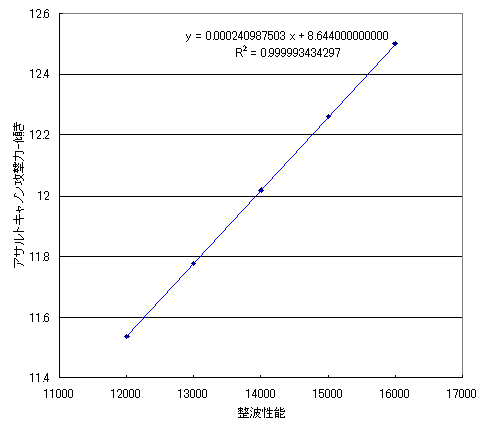
傾き-傾きは0.000241に近似されるためとりあえずよし。この場合のアサルトキャノン攻撃力の計算値は、

既に求められたとしているPA16000以外の実測値と計算値の平均誤差は1.361で実測値が少々過大評価でOK。最大誤差はPA15000でAA攻撃力/OBが5500での10.129、ここの領域では測定最大値を使用していたため問題ない。ただし、負の方向の最大誤差はPA12000、AA攻撃力/OBが5800での-6.090、たかだか攻撃力70000弱のうちの-6程度じゃないかと考えるかもしれませんが、実はここでの実測値も測定最大値です。試行回数も計算値に合わせようとだいぶ増やしたけれど足りない。一応同PAにおける、AA攻撃力/OBが6200の測定では誤差は-0.708と1未満に落ち着いているけれども。確実に傾向としては低PA側の方が実測値が計算値に対して小さめになっています。つまり、乱数を考慮しても、計算値はほんのわずかながら本当の内部計算式とはズレがあるだろうと推測されます。
候補をもうひとつ考えてみましょう。ここから先は、私自身も今日思いついたばかりで計画していなかった部分です。
先ほどは傾き-切片の有効数字は4桁でしたが、傾き-傾きの有効数字は3桁でした。では、傾き-傾き部分の有効数字も4桁に高めるならどうなるでしょうか。束縛条件Aを満たして、なおかつ傾き-傾き部分の有効数字も4桁のままである候補として、
候補その2…傾き-傾き=0.0002415、傾き-切片=8.636
があります。傾き-切片を8.636に補正した場合、

傾き-傾きは0.0002415に近似されるためよし。
計算値は、

平均誤差は6.688で過大評価でOK。候補1よりも増えているものの、測定最大値が多いため特に問題ない。最大誤差はPA15000でAA攻撃力/OBが5500での12.879で理由は先ほどと同様に許容範囲。この場合最小誤差は0.934で正の値。候補1とは異なり、乱数の捉え方を変えることで十分カバー可能な計算式です。というのは、アサルトキャノンの攻撃力差は最大で20程度(大抵10程度だけれど測定回数増やすと低頻度ながら出てくる)幅を持って確認されるからです。
候補1から、
アサルトキャノン攻撃力=(0.000241×PA+8.644)×AA攻撃力/OB+0.25×(PA-4000)+963(PA12000~16000)
候補2から、
アサルトキャノン攻撃力=(0.0002415×PA+8.636)×AA攻撃力/OB+0.25×(PA-4000)+963(PA12000~16000)
これ以外の候補を出すのは誤差が激しくなるため不可。有効数字をさらに増やすのも不本意のため却下。もしかしたらAAのときのように分数表記かもしれないが適当な値が思いつかず。
個人的には候補2に考えが傾きつつありますが、断言はできません。PA12000での傾きは、候補1の場合11.536、候補2の場合、11.534です。PA10000~12000での計算式次第でどちらか決定されるといいんですが、この小数点以下3桁目の精度がどうかといわれると正直なところPA10000とかやっても無理っぽい。ですので、意欲があれば(ここ重要)、PA12000について、乱数を十分考慮した上で候補2をカバーしきれるかどうか改めて詳しくやってみようと思います。PA12000さえカバー出来れば、PA16000が成立する前提から、PA13000~15000も近似式の傾きの関係で同様にカバー出来るはずです。
Part5.5Part4,5の式を改変
Part1アサルトキャノンのもろもろ性質とか。
Part1.5アサルトキャノン射程について。
Part2アサルトキャノン攻撃力のPA依存性について。
Part3アサルトキャノン攻撃力のAA攻撃力/OB依存性について。
Part3.01レギュ変化に伴い心機一転
Part4PA16000~19555でのアサルトキャノン攻撃力
Part5PA12000~16000でのアサルトキャノン攻撃力
Part5.5Part4,5における計算式の改変
Part6PA9000~12000でのアサルトキャノン攻撃力
Part7PA9000以下のアサルトキャノン攻撃力とまとめ
今回はPA12000~16000でのアサルトキャノン攻撃力(レギュ1.20)について。
測定条件は、アサルトキャノン発動側のPAが12000、13000、14000、15000になったぐらいで他は前回と一緒。PA16000部分は細部が異なる2種類の攻撃力計算式の切り替わりポイントのため、前回の数値を流用する。
まず実測値↓

特定PA、特定AA攻撃力/OBでの攻撃力。実はPA14000以下ぐらいから計算式のめぼしがついてきたため、計測基準が微妙に変化していたりします。PA16000、15000と14000の途中ぐらいまでは数回計測した最大値を使用、それ以外では最大値を使用していたり計算値に極めて近い値が出たらそれを使用していたりPA12000ではまた頑張って最大値を求めたりと割と適当だったり。その基準の変化が結果に及ぼす影響とかあるでしょうが、今回はそんなものよりも、私自身の解釈による比重が非常に大きいですのでよろしく。
グラフは、

表に記載されている「傾き」、「切片」というのは、↑のグラフの近似直線の傾きと切片を指します。
グラフ見るとわかりますが、整波性能を1000とか上げるよりも、OBをAA攻撃力の高いものに換えた方が攻撃力変化が大きいです。ただ、AA攻撃力4600以上はP-MARROWを装備する必要があるため、実現が容易かと言われるとそうでもない。
切片部分について、グラフとその近似式は、

PA16000~19555の前回では、切片の式は、0.25×(PA-4000)+963 (963:レギュ1.20現在のLETHALDOSEに設定されたアサルトキャノン攻撃力) と予測しました。今回もそれと同様の式と考えられ、良い近似を示します。最大値とか多く使っているため2とか3ぐらい過大評価されていても気にしない。個人的にはグラフから判断するなら966にしたいんだけれど表示スペックを尊重。
傾きについてですが、ここからゴリ押しなのでやばいです。普通に近似式を求めると、
傾きの近似式
=0.000241568×整波性能+8.635787284 R^2=0.999999271

前回、乱数を考慮しない状態で、
アサルトキャノン攻撃力=12.5×AA攻撃力/OB+0.25×(PA-4000)+963(PA16000~19555)
と求めました。これの精度については今更どうこう言いませんが、ここから束縛条件として、PA16000のとき
(傾き-傾き)×PA整波性能(16000)+(傾き-切片)=12.5…A
であると言えます。
傾きの値に着目すると、
11.5349747
↓
11.77595731
↓
12.01732009
↓
12.25932791
↓
12.5011304(12.5)
PAが1000増えるごとに、0.25よりは少ない変化量…ただし0.24よりは気持ち大きい変化量であることが分かります。
候補その1…傾き-傾き=0.000241、傾き-切片=8.644、これはAを満たす。
切片を8.644に補正する場合、

傾き-傾きは0.000241に近似されるためとりあえずよし。この場合のアサルトキャノン攻撃力の計算値は、

既に求められたとしているPA16000以外の実測値と計算値の平均誤差は1.361で実測値が少々過大評価でOK。最大誤差はPA15000でAA攻撃力/OBが5500での10.129、ここの領域では測定最大値を使用していたため問題ない。ただし、負の方向の最大誤差はPA12000、AA攻撃力/OBが5800での-6.090、たかだか攻撃力70000弱のうちの-6程度じゃないかと考えるかもしれませんが、実はここでの実測値も測定最大値です。試行回数も計算値に合わせようとだいぶ増やしたけれど足りない。一応同PAにおける、AA攻撃力/OBが6200の測定では誤差は-0.708と1未満に落ち着いているけれども。確実に傾向としては低PA側の方が実測値が計算値に対して小さめになっています。つまり、乱数を考慮しても、計算値はほんのわずかながら本当の内部計算式とはズレがあるだろうと推測されます。
候補をもうひとつ考えてみましょう。ここから先は、私自身も今日思いついたばかりで計画していなかった部分です。
先ほどは傾き-切片の有効数字は4桁でしたが、傾き-傾きの有効数字は3桁でした。では、傾き-傾き部分の有効数字も4桁に高めるならどうなるでしょうか。束縛条件Aを満たして、なおかつ傾き-傾き部分の有効数字も4桁のままである候補として、
候補その2…傾き-傾き=0.0002415、傾き-切片=8.636
があります。傾き-切片を8.636に補正した場合、

傾き-傾きは0.0002415に近似されるためよし。
計算値は、

平均誤差は6.688で過大評価でOK。候補1よりも増えているものの、測定最大値が多いため特に問題ない。最大誤差はPA15000でAA攻撃力/OBが5500での12.879で理由は先ほどと同様に許容範囲。この場合最小誤差は0.934で正の値。候補1とは異なり、乱数の捉え方を変えることで十分カバー可能な計算式です。というのは、アサルトキャノンの攻撃力差は最大で20程度(大抵10程度だけれど測定回数増やすと低頻度ながら出てくる)幅を持って確認されるからです。
候補1から、
アサルトキャノン攻撃力=(0.000241×PA+8.644)×AA攻撃力/OB+0.25×(PA-4000)+963(PA12000~16000)
候補2から、
アサルトキャノン攻撃力=(0.0002415×PA+8.636)×AA攻撃力/OB+0.25×(PA-4000)+963(PA12000~16000)
これ以外の候補を出すのは誤差が激しくなるため不可。有効数字をさらに増やすのも不本意のため却下。もしかしたらAAのときのように分数表記かもしれないが適当な値が思いつかず。
個人的には候補2に考えが傾きつつありますが、断言はできません。PA12000での傾きは、候補1の場合11.536、候補2の場合、11.534です。PA10000~12000での計算式次第でどちらか決定されるといいんですが、この小数点以下3桁目の精度がどうかといわれると正直なところPA10000とかやっても無理っぽい。ですので、意欲があれば(ここ重要)、PA12000について、乱数を十分考慮した上で候補2をカバーしきれるかどうか改めて詳しくやってみようと思います。PA12000さえカバー出来れば、PA16000が成立する前提から、PA13000~15000も近似式の傾きの関係で同様にカバー出来るはずです。
Part5.5Part4,5の式を改変









