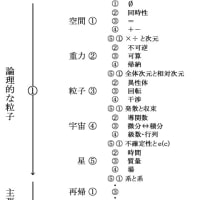
『可算濃度と連続体濃度の間には他の濃度が存在しない』
濃度という規定がある時点で、ここで何を言っても素人考えになりそうだが、存在しないなら作ればいいのではないか?
まずは数の定義。
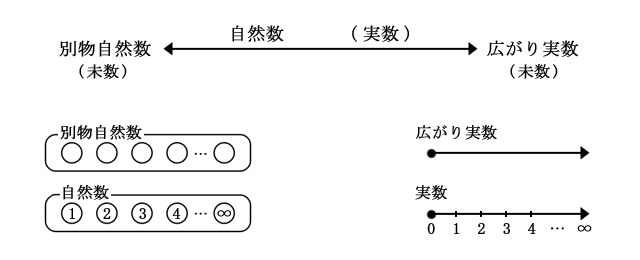
未数は数ではなく、数になる前のもの。
○別物自然数:存在するだけでは数にならない。存在を方向性に沿って並べることで数になる。
○広がり実数:連続する無限の広がり、つまり重力。広がりそのものは数ではない。
別物自然数と広がり実数が互いに観測し合って、数は数となる。
自然数は、別物自然数を広がり実数の性質を使って数えられるようにしたもの。
実数は、広がり実数を自然数の性質を使って計れるようにしたもの、と言いたいところだが、ここに大きな問題がある。
実のところ、実数というのは、計算によって導き出されたものにすぎない。しかも、別々の方法で導き出された数が、同じ数軸上に並べられると仮定しているだけ。
自然数が連続体でないのはわかるが、実数に濃度があるかどうかは疑わしい。
これがありなら、自然数から実数ではない数もつくれそうだが、もはや濃度では比べられそうもない。
問題は、実数を定義する方法がないことにあるのだと思う。だから濃度という考え方をもとに、自然数を使って実数を定義しようとした。これがうまくいかなかったってことは、実数に問題があるってことだ。
※2つの無理数を、数を比べることなしに、どちらが大きいか判定することはできるのか?
※実数に含まれるすべての数を表すことができる計算式はあるのか? その式さえあればどんな無理数でも何桁でも表すことができ、しかもその無理数を導く他の計算式とも互換性がある。
実際は、実数の中に無理数が並んでいると想定しているだけで、そのほとんどが存在を確認することすらできないのではないか?