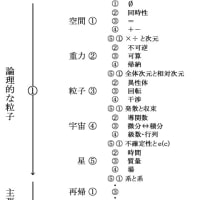
世の中には半次元で表せるものが2つある。時間と光である。
光は直進するだけなら半次元あればいい。さらにいえば、±1で直進し、±iで留まる、虚数次元という考え方もできる。
半次元は1次元の下にある。たとえば3次元に2次元や1次元が含まれるように、ただの1次元は半次元を含んでの1次元となる。このことは4次元でも5次元でも同じ。もちろん3次元にも半次元が含まれている。
ところが半次元は他の次元と違って半分しかない。他の次元と同じように計算するには工夫がいるのは目に見えている。
とくに半次元=虚数次元だとすると、大きさが∞=1となって問題になりそう。
ただし、数学で虚数が複素数として扱われるだけなら、まだやりようはありそう。
a+bi これってただの符号?
大きさの問題も次のように考えられる。
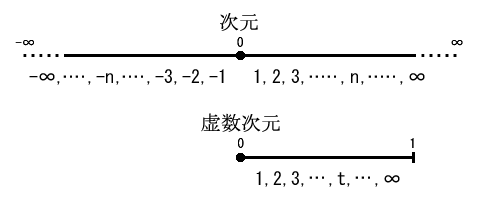
普通の次元は自然数に対応させた数え方。虚数次元は自然数で分割した数え方。
虚数次元は次元の単位として1として扱われるが、大きさは∞であり、他の次元と異質のものではない。
以上のことをふまえ、虚数次元を含んだ次元の計算がどんなものになるか。
1,2,3,…,n の次元軸と垂直方向に、1/(1,2,3,…,n) の次元軸が半分だけあるのだから、普通に計算できるとは思えない。
その一つの答えになりそうなのが時空の計算である。
3次元に時間の半次元?を加えて計算する。ローレンツ変換を使うのだそうだが。
ウィキペディアで時空の説明を読んでもさっぱり理解できなかった。
と、わからないなりに大きな疑問。3次元に半次元を加えても、それはもともと3次元に含まれるものなので、時間を変化させて計算しているように見えて、実は時間はまったく動いていないのではないか?
ついでにもう一点、時間を半次元として計算する場合、虚数を2回掛ければ、マイナス方向への時間も計算できるようになる?