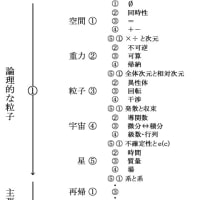
① １＋１＝２② ｎ＝１、ｎ＝ｎ＋１ → ｎ＝｛１、２、３、４、…｝ ①の計算は同時に処理される。光が最速で、光の速度で計算されるので、まだ計算されていないから正しい答えが出せない、とはならない。 一方、②の計算は、同時に処理してしまうと、∞という結果しか残らない。 まず①の計算について、計算が同時に処理されるということは、そこにあるのは正しい計算かどうかということだけ。そして、正しい計算は、数の性質を表している。 しかし、式の各項目が正しいという保証は、式の中では担保されていない。 一方、②の計算は、繰り返しによって数を生み出しているように見えても、これが数の性質と合致するかどうかは①で計算してみないとわからない。 ①は数の性質を表すだけ。②は繰り返しで答えを生み出すだけ。 数とは、①と②が補い合って生み出されたもの、ということになる。
※注意点 ①は正確には、正しい計算は次元の性質を表していること。 最も注意すべきは、数はその繰り返しにおいてのみ正しいということ。たとえば…
これをどこまで同じ数として扱えるか。 数学的な直線、真円は次元の中にあるが、その次元自体が歪んでいるということもありうる。 数学の中には規則正しい繰り返しがあるが、繰り返し自体に規則的である根拠がない。 繰り返しがズレて、次元の性質と合致しなくなるまでズレたとして、それが本当に繰り返しといえるのかどうかはまた別の問題。 繰り返しの結果が次元の性質と合致して連続しているように見えて、本当にそう見えるだけということも。
