なんでこうなるの

http://abc-analytics.com/decision-on-a-abtest-from-smart-bear-blog
「ABテストと統計数字(A smart bearのblogから)」なんだけど...ひどい...

冒頭から，いきなり

> カイ二乗値が4より上の組み合わせ（A,Bの回数)を緑色にしてる。
> ちなみに、カイ二乗が自由度１で値が３の時、p値は0.92。4で0.97くらい？

おいおい，それは，p 値ではなく，上側確率だし，p 値は「ある値以上の値を取る確率」なんだから，pchisq(1, 1, lower.tail=FALSE) = 0.08326452
でしょうが。

> 自由度１のカイ二乗値が6.15の場合は、98-99%の有意水準になります。

むちゃくちゃですね。
なんか，データをとって，カイ二乗検定をやって，カイ二乗値=6.15で，自由度が1 なら，
pchisq(6.15, 1, lower.tail=FALSE)
[1] 0.01314121
です。有意水準 5% のもとで，両側検定をした結果は，以下のように述べられます。

カイ二乗検定の結果，カイ二乗値は 6.15（自由度 1）となり，有意確率（p 値）は 0.013 で，有意水準 5% のもとで有意である。

> 僕を含めた大部分の人は統計が苦手。だって直感じゃだめだから。そこで、英語で書かれたblogで良い記事を見つけたので、紹介します。

って，いいわけをすればいいわけじゃないのだ

この記事を，「参考になる」として，あげている人もいるのだから，被害はあなただけじゃない

騙されてはいけませんよ

http://blog.share-wis.com/?p=359
「誰でも簡単にA/Bテストが作れるOptimizelyを実際に使ってみた」なんだけど...

オンラインツールを使って A/B テストを実際にやってみた結果の図が掲示されている。



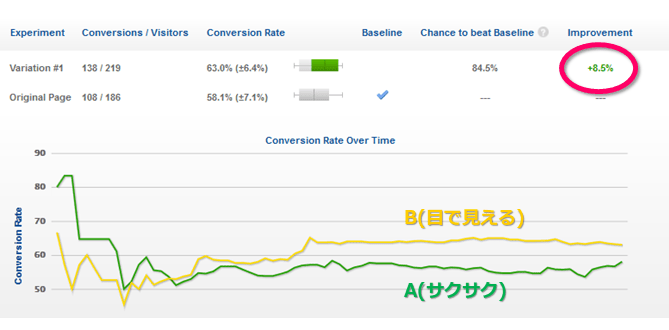
(1) B: 138/219 = 63.4%(±6.4%) と A: 108/186 = 58.1%(±7.1%)で 8.5% 増という結果になった

独立二標本の比率の差の検定は，以下のようになり，有意差があるとはいえない結果である。後述(4)は怪しいものだということが分かる。

「8.5% 増」というのは，(63.0 - 58.1)/58.1*100≒8.5 ということであろうが，数字のマジックというか，パーセントのパーセントを取るというのも結果をよく見せる詐欺的手法ではないか？パーセントの差は 4.9% なんだから。改善率でいうか改善度でいうかの違いで，かなり印象が違う。

(2) テスト人数を増やせば統計的有意性が出るようになるのではないかと期待して，テストを走らせ続けていたが，費用がかかるので，ここで止めた

図を見れば，終了直前当たりで A が増え始めたように見えるが，テスト期間の中頃以降はほぼ同じレベルで推移していることが分かる。つまり，A, B の母比率はほぼ終了時の値とみてよいということであろう。母比率が 138/219 と 108/186 のままで，A, B の分母の割合も 219:186 のままで，このテストが継続されると，いずれは「A，B に有意な差がある」という結果になるのは確かである。では，どれくらいになったら有意になるのか。数式を解いてもよいが，ちょいちょいとシミュレーションする方が速いのでやってみると，3.7 倍くらいのサンプルサイズになって，A: 516/818，B:403/695 でやっと「有意水準 5% のもとで，A，B に差がある」という結果になる。ずいぶんなサンプルサイズだこと！当然といえば当然で，4.9% 位の「差」を検出するにはそれくらいのサンプルサイズが必要ということである。比率の差の大きさを抜きにして(4)でいうような「100である程度有意性が確保される」は，全くのはったりである。そんなことを信じてはいけませんよということ。
テストを行う前から A，B の差を知ることはできないがテストを行ってしばらくたつと（図で表されてる真ん中以降で，比率がほぼ安定するあたりのこと），母比率の目安がつくので，その時点でパワー・アナリシスを行うことをお勧めする。検出力を 0.8 として，他はデフォルトで，以下のようになる。

> power.prop.test(p1=138/219, p2=108/186, power=0.8)

     Two-sample comparison of proportions power calculation

              n = 1529.815 <<<< ここここ！
             p1 = 0.630137
             p2 = 0.5806452
      sig.level = 0.05
          power = 0.8
    alternative = two.sided

NOTE: n is number in *each* group <<<< ここここ！

驚くべきことに，片方ずつで 1530，両方ではその 2 倍だから 3060 のサンプルサイズが必要になるということである。コンバージョンは900前後ですよ。「え？，A: 516/818，B:403/695 でよかったんじゃないの？」ですって？現実は，そんな比例配分で事が済むわけではないので，パワー・アナリシスの方が正しいと見積もる方がよいと思いますね。

(3) あまり費用をかけずにテストを実行したい場合、統計的にある程度有意な結果が得られたらテストを止め、別のテスト開始する、というのが賢い使い方のようだ

そうともいえるし，そうでないともいえる。
純粋に統計学に従うと，とんでもなく時間と費用がかかるということが分かったら（分かるようにはしなくてはならない），さっさとケツまくって，逃げるに越したことはない。

(4) サービス提供会社は，「100コンバージョン/作成したページで統計的にある程度の有意性が確保される」と説明されている

これは，全くのウソ。クライエントを騙して金をむしり取ろうとする，悪徳商人だね。

まずは，A，B それぞれがどれくらいの割合なのかを何通りか試算して，パワー・アナリシスをやってみて，そのテストを実際にやるかどうか決めるとよい。

> power.prop.test(p1=0.5, p2=0.45, power=0.8)
              n = 1564.672
> power.prop.test(p1=0.10, p2=0.05, power=0.8)
              n = 434.432
> power.prop.test(p1=0.05, p2=0.04, power=0.8)
              n = 6744.933
NOTE: n is number in *each* group