金山発掘（馬鹿馬鹿し）

締め切りが 11/01 12:00 AM なので，その 1 分後に登録されるように予約する

問題

あなたは誕生日プレゼントとして、土地をもらえることになりました。
もらえる土地は、5×5マスの正方形の土地です。
世界は10×10のマスでできており、いくつかのマスには金山があります。金山の数が最大になる5×5マスは、1つしかありません。
最も多くの金山をゲットできるように、もらえる土地を探索するプログラムを書いてください。

例

以下、入力の例です。左上を {"x":0,"y":0} として、右下を {"x":9,"y":9} とします。「x」はx座標、「y」はy座標です。通常の土地は「w」の文字、金山のある土地は「G」の文字です。
これらは標準入力から、改行で区切られた文字として渡されます。

wwGwwwwwGG
Gwwwwwwwww
wwwwwwwwww
Gwwwwwwwww
wwwwGwwGww
wGwwwwwwww
wwwGGwwwww
wwwwwwGwww
wwwwGGwwww
GwwwGGwGwG

以下、出力の例です。最も多くの金山が得られる土地の左上の座標を、「{"x":3,"y":5,"g":8}」のように答えます。「x」はx座標、「y」はy座標、「g」は5×5マスの土地に含まれる金山の数です。
答えは、以下のように標準出力に出力してください。
{"x":3,"y":5,"g":8}

==========

プログラム自体は馬鹿馬鹿しいほど簡単なので，文字数を少なくするプログラムを目標にすると，以下のようなプログラムになった。

func = function(s) {
    x = matrix(unlist(strsplit(s, "")) == "G", byrow=TRUE, ncol=10)
    y = sapply(0:35, function(i) sum(x[i%%6+1:5, i%/%6+1:5]))
    i = which.max(y)-1
    cat(sprintf('{"x":%s,"y":%s,"g":%s}', i%/%6, i%%6, y[i+1]))
}
func("wwGwwwwwGGGwwwwwwwwwwwwwwwwwwwGwwwwwwwwwwwwwGwwGwwwGwwwwwwwwwwwGGwwwwwwwwwwwGwwwwwwwGGwwwwGwwwGGwGwG")

> func(s)
{"x":3,"y":5,"g":8}

投影図から想像する立体

投影図から想像する立体
締め切りが 2016/11/01 10:00 AM なので，その 1 分後に投稿されるように予約

設問

3次元の物体を図面に表すとき、投影図を使うことがあります。
例えば、図の左側のようにブロックが積まれているとき、上面図・側面図・正面図を矢印の方向から見た図で考えると、
図の右側のようになります。

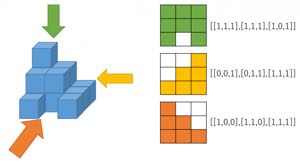
このとき、ブロックが見える位置を「1」、見えない位置を「0」とし、上の段から順に右のように表現します。

この上面図、側面図、正面図の表現が標準入力から与えられるとき、考えられるブロックの配置が何通りあるかを求め、
標準出力に出力してください。
なお、入力のサイズはいずれの面も3×3で固定とします。
また、ブロックの下には必ずブロックが必要で、空中に浮くブロックはないものとします。

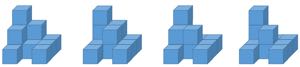
例えば、上記の場合は他に以下のパターンがあり、全部で5通りですので、
以下のように出力します。

【入出力サンプル】
標準入力
[[1,1,1],[1,1,1],[1,0,1]]
[[0,0,1],[0,1,1],[1,1,1]]
[[1,0,0],[1,1,0],[1,1,1]]

標準出力
5

与えられた入力でブロックを配置できない場合は0を出力してください。

＝＝＝＝＝＝＝＝

ブルートフォースでは 2 番目の入力例には無理だなあ

f = function(A, B, C) {
    B = B[3:1, 3:1]
    C = C[3:1, ]
    count = 0
    D = array(integer(27), dim=c(3,3,3))
    x = rbind(c(0L, 0L, 0L), c(1L, 0L, 0L), c(1L, 1L, 0L), c(1L, 1L, 1L))
    q = sum(A) == 27
    for (i1 in 1:4) {
        if (A[1,1] == 0 && i1 >= 2) break
        if (A[1,1] == 1 && i1 == 1) next
        D[1:3] = x[i1, ]
        if (sum(D[1:3] & !B[1:3])) break
        if (i1 == 1 && sum(B[1:3])) next
        for (i2 in 1:4) {
            if (A[2,1] == 0 && i2 >= 2) break
            if (A[2,1] == 1 && i2 == 1) next
            D[4:6] = x[i2, ]
            if (sum(D[4:6] & !B[4:6])) break
            for (i3 in 1:4) {
                if (A[3,1] == 0 && i3 >= 2) break
                if (A[3,1] == 1 && i3 == 1) next
                D[7:9] = x[i3, ]
                if (sum(D[7:9] & !B[7:9])) break
                for (i4 in 1:4) {
                    if (A[1,2] == 0 && i4 >= 2) break
                    if (A[1,2] == 1 && i4 == 1) next
                    D[10:12] = x[i4, ]
                    for (i5 in 1:4) {
                        if (A[2,2] == 0 && i5 >= 2) break
                        if (A[2,2] == 1 && i5 == 1) next
                        D[13:15] = x[i5, ]
                        for (i6 in 1:4) {
                            if (A[3,2] == 0 && i6 >= 2) break
                            if (A[3,2] == 1 && i6 == 1) next
                            D[16:18] = x[i6, ]
                            for (i7 in 1:4) {
                                if (A[1,3] == 0 && i7 >= 2) break
                                if (A[1,3] == 1 && i7 == 1) next
                                D[19:21] = x[i7, ]
                                for (i8 in 1:4) {
                                    if (A[2,3] == 0 && i8 >= 2) break
                                    if (A[2,3] == 1 && i8 == 1) next
                                    D[22:24] = x[i8, ]
                                    for (i9 in 1:4) {
                                        if (A[3,3] == 0 && i9 >= 2) break
                                        if (A[3,3] == 1 && i9 == 1) next
                                        D[25:27] = x[i9, ]
                                        if (all((apply(D, c(2, 3), sum) > 0) == A,
                                                (apply(D, c(1, 2), sum) > 0) == B,
                                                (apply(D, c(1, 3), sum) > 0) == C)) {
                                            count = count+1
                                        }
                                    }
                                }
                            }
                        }
                    }
                }
            }
        }
    }
    cat(count)
}

system.time({
f(matrix(c(1,1,1,1,1,1,1,0,1), byrow = TRUE, ncol = 3),  # 5
  matrix(c(0,0,1,0,1,1,1,1,1), byrow = TRUE, ncol = 3),
  matrix(c(1,0,0,1,1,0,1,1,1), byrow = TRUE, ncol = 3))
})
system.time({
f(matrix(c(1,1,1,1,1,1,1,1,1), byrow = TRUE, ncol = 3), # 4051
  matrix(c(1,1,1,1,1,1,1,1,1), byrow = TRUE, ncol = 3),
  matrix(c(1,1,1,1,1,1,1,1,1), byrow = TRUE, ncol = 3))
})
system.time({
f(matrix(c(1,0,1,0,1,0,1,0,1), byrow = TRUE, ncol = 3), # 17
  matrix(c(1,1,1,1,1,1,1,1,1), byrow = TRUE, ncol = 3),
  matrix(c(1,1,1,1,1,1,1,1,1), byrow = TRUE, ncol = 3))
})
system.time({
f(matrix(c(1,1,1,1,0,1,1,1,1), byrow = TRUE, ncol = 3), # 104
  matrix(c(0,0,0,1,1,1,1,1,1), byrow = TRUE, ncol = 3),
  matrix(c(0,0,0,1,1,1,1,1,1), byrow = TRUE, ncol = 3))
})
system.time({
f(matrix(c(1,1,1,0,1,0,1,1,1), byrow = TRUE, ncol = 3), # 0
  matrix(c(0,1,0,1,1,1,1,0,1), byrow = TRUE, ncol = 3),
  matrix(c(1,0,1,1,1,1,0,1,1), byrow = TRUE, ncol = 3))
})