Julia に翻訳--167 多角形の面積

#==========
Julia の修行をするときに，いろいろなプログラムを書き換えるのは有効な方法だ。
以下のプログラムを Julia に翻訳してみる。

多角形の面積
http://aoki2.si.gunma-u.ac.jp/R/area.html

ファイル名: area.jl　　関数名: area

翻訳するときに書いたメモ

添え字の最後が end で表せてうれしい！というのはあまりない。
このプログラムではわざわざ n = size(xy, 1) とするのを避けることができる。

==========#

function area(xy)
    x = xy[:, 1]
    sum((vcat(x[2:end], x[1]) - vcat(x[end], x[1:end-1])) .* xy[:, 2]) / 2
end

xy = [9 4; 7 5; 6 4; 7 2; 5 1; 2 3; 3 4; 1 5; 1 7; 3 7; 4 6; 7 8];
area(xy) # 28.5

x = range(0, 1.96, length = 100)
using Rmath
y = vcat(0, dnorm.(x), 0);
x = vcat(0, x, 1.96);
area(hcat(x, y)) # 0.47499836347526403

x = range(0, 1.96, length = 100000)
y = vcat(0, dnorm.(x), 0);
x = vcat(0, x, 1.96);
area(hcat(x, y))  # 0.47500206810889967

pnorm(1.96) - 0.5 # 0.4750021048517796

Julia に翻訳--166 3次式方程式の解

#==========
Julia の修行をするときに，いろいろなプログラムを書き換えるのは有効な方法だ。
以下のプログラムを Julia に翻訳してみる。

3次式方程式の解
http://aoki2.si.gunma-u.ac.jp/R/cubic.html

ファイル名: cubic.jl　　関数名:cubic

翻訳するときに書いたメモ

このシリーズでは，複素数ははじめて取り扱う。

==========#

function cubic(a, b, c, d)
    cubicroot(x) = sign(x) * abs(x) ^ (1 / 3)
    a != 0 || error("3次の項の係数がゼロです")
    b = b / (3 * a)
    c = c / a
    d = d / a
    p = b ^ 2 - c / 3
    q = (b * c - 2 * b ^ 3 - d) / 2
    a = q ^ 2 - p ^ 3
    if a == 0
        q = cubicroot(q)
        res = [2 * q - b, - q - b]
    elseif a > 0
        a3 = cubicroot(q + sign(q) * sqrt(a))
        b3 = p / a3
        x = (-(a3 + b3) / 2 - b) + (abs(a3 - b3) * sqrt(3) / 2)im
        res = [a3 + b3 - b, x, conj(x)]
    else
        a = 2 * sqrt(p)
        t = acos(q / (p * a / 2))
        res = [a * cos(t / 3) - b, a * cos((t + 2π) / 3) - b, a * cos((t + 4π) / 3) - b]
    end
    res
end

cubic(1, 1, 1, 1)
# 3-element Vector{ComplexF64}:
#                   -1.0 + 0.0im
#  5.551115123125783e-17 + 0.9999999999999999im
#  5.551115123125783e-17 - 0.9999999999999999im

cubic(1, -5, 7, -3)
# 3-element Vector{ComplexF64}:
#  3.0000000000000004 + 0.0im
#  0.9999999999999999 + 1.530319146620381e-8im
#  0.9999999999999999 - 1.530319146620381e-8im

cubic(1, -1, 2, 1)
# 3-element Vector{ComplexF64}:
#  -0.3926467817026407 + 0.0im
#   0.6963233908513203 + 1.4359498641099562im
#   0.6963233908513203 - 1.4359498641099562im

cubic(0, 1, 1, 1)
# 3次の項の係数がゼロです

Julia に翻訳--165 二分法による 1 変数方程式の解

#==========
Julia の修行をするときに，いろいろなプログラムを書き換えるのは有効な方法だ。
以下のプログラムを Julia に翻訳してみる。

二分法による 1 変数方程式の解
http://aoki2.si.gunma-u.ac.jp/R/bisection.html

ファイル名: bisection.jl　　関数名: bisection， bisection2

翻訳するときに書いたメモ

さすがに，引数の個数・型が同じだと，同じ関数名では作れない。

==========#

function bisection(func, lower, upper; ndiv=1, epsilon = 1e-14, maxiteration = 500)
    if ndiv == 1
        root = bisection2(func, lower, upper)
        !isnan(root) && println("answer = $root")
        return root
    else
        x = range(lower, upper, length = ndiv)
        root = [bisection2(func, x[i], x[i + 1]; epsilon, maxiteration) for i = 1:ndiv - 1]
        n = length(root)
        if n == 0
            println("no solution")
        else
            root = root[.!isnan.(root)]
            for i in root
                println("answer = $i")
            end
            return root
        end
    end
end

function bisection2(func, lower, upper; epsilon = 1e-14, maxiteration=500)
    yl = func(lower)
    yu = func(upper)
    yl * yu > 0 && return NaN
    for i in 1:maxiteration
        mid = (lower + upper) / 2
        ym = func(mid)
        if abs(ym) < epsilon
            return mid
        elseif yu * ym > 0
            upper = mid
            yu = ym
        else
            lower = mid
            yl = ym
        end
        abs(upper - lower) < epsilon && return (lower + upper) / 2
    end
    NaN
end

func(x) = (x + 6.7) * (x - 3.4) * (x - sqrt(2))
bisection(func, -10.0, 10.0, ndiv=500)
bisection(x -> (x + 6.7) * (x - 3.4) * (x - sqrt(2)), -10, 10, ndiv=10)
# answer = -6.7
# answer = 1.4142135623730976
# answer = 3.4000000000000012

bisection(func, -10, 10)
# answer = -6.700000000000004

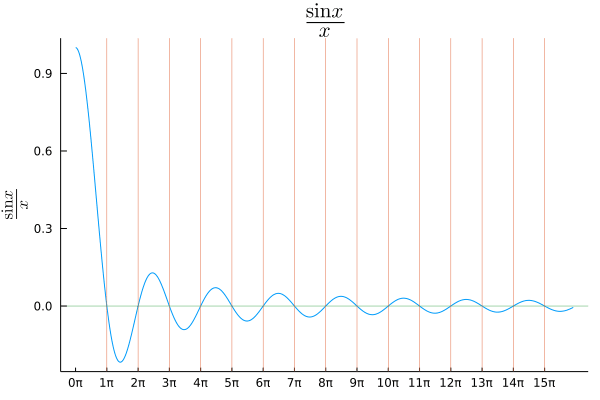
roots = bisection(x -> sin(x) / x, 0.0000001, 50, ndiv=100)
# answer = 3.1415926535897847
# answer = 6.2831853071795445
# answer = 9.424777960769305
# answer = 12.566370614359183
# answer = 15.707963267949054
# answer = 18.849555921538926
# answer = 21.991148575128346
# answer = 25.13274122871822
# answer = 28.274333882308085
# answer = 31.415926535897967
# answer = 34.557519189487856
# answer = 37.69911184307725
# answer = 40.84070449666758
# answer = 43.98229715025701
# answer = 47.123889803847334

using Plots
x = 0:0.01:50
plot(x, sin.(x) ./ x, grid=false, ylabel="\$\\frac{\\sin x}{x}\$", title="\$\\frac{\\sin x}{x}\$", label="");
x = 0:15
xticks!(π .* x, string.(x) .* "π")
vline!(roots, lw=0.5, label="");
hline!([0], lw=0.5, label="");
savefig("fig1.png")