算額(その1536)
(12) 京都市伏見区御香宮門前町 御香宮神社(ごこうのみやじんじゃ)文久3年(1863)
近畿数学史学会:近畿の算額「数学の絵馬を訪ねて」,平成4年5月16日 初版第一刷,大阪教育図書株式会社,大阪市.
キーワード:円4個,水平線,斜線2本
#Julia, #SymPy, #算額, #和算
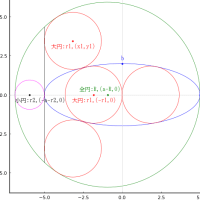
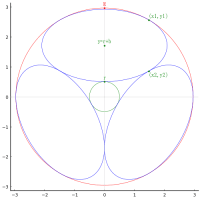
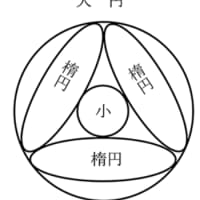
3 本の直線で区画された領域に,大円,中円,小円,天円を容れる。大円,中円,天円の直径がそれぞれ 85 寸,25 寸,8 寸のとき,小円の直径はいかほどか。

中円の直径を d1
大円の直径を d3
天円の直径を d4
小円の直径を d2
として,算法助術の公式62を用いる。
using SymPy
@syms d1, d2, d3, d4
eq62 = -d1*d2*d3 + (d1 + d2)*d3*d4 + d1*d2*d4;
solve(eq62, d2)[1] |> println
d1*d3*d4/(d1*d3 - d1*d4 - d3*d4)
小円の直径は d2 = d1*d3*d4/(d1*d3 - d1*d4 - d3*d4) である。
ans_d2 = solve(eq62(d1 => 25, d3 => 85, d4 => 8), d2)[1].evalf()
ans_d2 |> println
13.6546184738956
d1, d3, d4 に具体値を代入して d2 = 13.6546184738956 である。