算額(その1132)
七十八 岩手県藤沢町藤沢早道 竹駒神社 元治2年(1865)
山村善夫:現存 岩手の算額,昭和52年1月30日,熊谷印刷,盛岡市.
http://www.wasan.jp/yamamura/yamamura.html
キーワード:円1個,正三角形,正方形
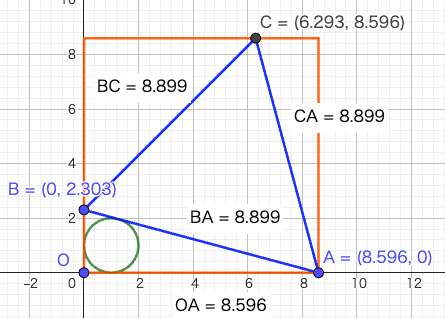
正方形の中に円と正三角形を容れる。円の直径が 2 寸のとき,正三角形の一辺の長さはいかほどか。

正方形の一辺の長さを a
円の半径と中心座標を r, (r, r)
とおき,以下の連立方程式を解く。
正三角形の一辺の長さは sqrt(a^2 + b^2) である。
include("julia-source.txt")
using SymPy
@syms a::positive, b::positive, c::positive,
r::positive
eq1 = a + b - sqrt(a^2 + b^2) - 2r
eq2 = a^2 + b^2 - (c^2 + (a - b)^2)
eq3 = a^2 + b^2 - ((a - c)^2 + a^2)
res = solve([eq1, eq2, eq3], (a, b, c))[1]
res |> println
(r*(-sqrt(3) - 1)/(-sqrt(3) + sqrt(2)), r*(1 - sqrt(3))/(-sqrt(3) + sqrt(2)), -2*r/(-sqrt(3) + sqrt(2)))
@syms d
#= a =# apart(res[1]) |> simplify |> println
r*(sqrt(2) + sqrt(3) + sqrt(6) + 3)
#= b =# apart(res[2]) |> simplify |> println
r*(-sqrt(3) - sqrt(2) + sqrt(6) + 3)
#= c =# apart(res[3]) |> simplify |> println
2*r*(sqrt(2) + sqrt(3))
length = sqrt(res[1]^2 + res[2]^2) |> simplify |> apart |> simplify
length |> println
length(r => 2/2).evalf() |> println
2*r*(2 + sqrt(6))
8.89897948556636
正三角形の一辺の長さ length は,円の半径 r の 4 + 2√6 倍である。
円の直径が 2 寸のとき,正三角形の一辺の長さは 8.89897948556636 である。
「答」,「術」も間違っているし,それを間違っていると言っている山村も間違った答えを出している。
図を描いてみればわかること。
function draw(r, more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
a = r*(√2 + √3 + √6 + 3)
b = r*(-√3 - √2 + √6 + 3)
c = 2r*(√2 + √3)
length = 2r*(2 + √6)
@printf("円の直径が %g のとき,正三角形の一辺の長さは %g である。\n", 2r, length)
@printf("r = %g; a = %g; b = %g; c = %g\n", r, a, b, c)
plot([0, a, a, 0, 0], [0, 0, a, a, 0], color=:green, lw=0.5)
circle(r, r, r)
plot!([0, a, c, 0], [b, 0, a, b], color=:blue, lw=0.5)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(a, 0, " a", :green, :left, :bottom, delta=delta/2)
point(0, b, "b ", :green, :right, :vcenter)
point(c, a, "(c, a)", :green, :center, :bottom, delta=delta/2)
xlims!(-5delta, a + 3delta)
end
end;



























