算額(その1555)
六十三 岩手県花泉町 大門神社・大門観世音菩薩 明治13年(1880)
山村善夫:現存 岩手の算額,昭和52年1月30日,熊谷印刷,盛岡市.
http://www.wasan.jp/yamamura/yamamura.html
キーワード:円7個,斜線2本
#Julia, #SymPy, #算額, #和算, #数学
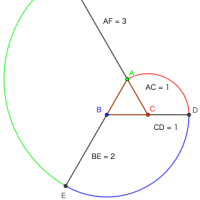
大円と 2 本の斜線で区分される領域に 6 個の小円を描く。小円の直径が 1 寸のとき黄積はいかほどか。
大円の半径と中心座標を r1, (0, 0)
小円の半径と中心座標を r2, (r1 - r2, 0), (x2, y2), (x3, y3)
とおく。
「大円の直径はいかほどか」という場合は,算額(その1554)四十 岩手県一関市牧沢 牧沢八幡神社 明治5年(1872)の類題として解ける。この場合も,大円の直径は小円の直径の 4 倍である。
さて,山村は黄積を小円と大円の間にできる狭い領域(図のピンクと緑)も含めて色を塗っている。しかし,それでは答えが合わない。

正しくは,「日本の弦と小円の弧で囲まれる領域 ABCG の 2倍」である。OCE は ODG と相似なので,図に示した黄色の部分の面積は,「長方形 ABCD から,小円 1 個分の面積を差し引いた面積」である。

BC は小円の直径であるが,AB は何か?
三角形OCH において θ = ∠COH とすると,CH = sin(θ) = r2/3r2 = 1/3 なので θ = asin(1/3), OC = 3r2*cos(θ) = 3r2*cos(asin(1/3)) = 2√2r2 である。BC は 4√2*r2 である。
長方形 ABCD の面積 = 2r2 * 2√2*2r2
小円 1 個分の面積 = πr2^2
黄積 = 「2*(長方形 ABCD の面積」 - 「小円 1 個分の面積」)
= 2(2r2 * 2√2*2r2 - π*r2^2)
= 2(8√2 - π)*r2^2
小円の半径が 1/2 のとき,黄積は 4.086057922697484 である。
r2 = 1/2
2(8√2 - π)*r2^2
4.086057922697484
術は,「(√32 - 2*円積率)×小円径」で,円積率として π/4 を使い,小円の直径が 1 のとき,(√32 - 2*π/4)*1 = 4.086057922697484 で,答え 4.086余 となっている。
上述の結果と同じである。
山村は,オウム返しで術の解説をしているだけで,実際に解いていない。山村が理解した黄積で計算を進めたら,術と一致しないのだから。

include("julia-source.txt");
# julia-source.txt ソース https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf
using SymPy
@syms a::negative, r1::positive, r2::positive,
x2::positive, y2::positive,
x3::negative, y3::positive;
eq1 = -(r1 - 2r2)/a - r2/(r1 - r2)
eq2 = -r2/(r1 - r2 + a) - r2/(r1 - r2)
eq3 = x2^2 + y2^2 - (r1 - r2)^2
eq4 = (r1 - r2 - x2)^2 + y2^2 - 4r2^2
res = solve([eq1, eq2, eq3, eq4], (r1, a, x2, y2))[1]
(4*r2, -6*r2, 7*r2/3, 4*sqrt(2)*r2/3)
大円の半径は,小円の半径の 4 倍である。
以下は,上下の円を描くために必要な円の中心を求めるための計算。
@syms θ
r1 = 4r2
a = -6*r2
θ = asin(r2/(r1 - r2 + a))
eq5 = x3^2 + y3^2 - (r1 - r2)^2
eq6 = dist2(a, 0, 0, a*tan(θ), x3, y3, r2)
res2 = solve([eq5, eq6], (x3, y3))[1] # 1 of 3
(-r2, 2*sqrt(2)*r2)
function draw(r2, more)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
r1 = 4r2
(r1, a, x2, y2) = (4*r2, -6*r2, 7*r2/3, 4*sqrt(2)*r2/3)
(x3, y3) = (-r2, 2*sqrt(2)*r2)
plot()
circle(0, 0, r1, :magenta)
circle2(r1 - r2, 0, r2)
circle22(x2, y2, r2)
circle22(x3, y3, r2)
slope = tan(asin(r2/(r1 - r2 + a)))
abline(a, 0, slope, 1.05a, r1 + 2r2, :green)
abline(0, 0, -slope, 1.05a, r1 + 2r2, :blue)
abline(2a, 0, -slope, 1.05a, r1 + 2r2, :blue)
abline(a, 0, -slope, 1.05a, r1 + 2r2, :green)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(r1 - r2, 0, "r1-r2", :red, :center, delta=-delta/2)
point(r1, 0, " r1", :red, :left, delta=-delta/2)
end
end;
draw(1/2, true)