「ループ・トラッキング」問題

「ループ・トラッキング」問題

締め切りが 2017/10/26 10:00 AM なので，その 1 分後に投稿されるように予約

自然数 n に対し、関数 Fn(x) を次のように定義します（floor()：床関数）。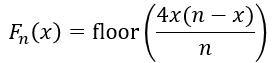

例えば n＝10, x＝1 のとき、F10(1) ＝ floor(4×1×9÷10) ＝ 3 です。
 
さて、整数 k（0 ≦ k ≦ n）に対して、関数 Fn による変換を繰り返し行います。
例えば n＝10, k＝1 のとき、F10 で 1 を変換すると 3 となり、さらに変換すると 8 となります。
以降、1 → 3 → 8 → 6 → 9 → 3 → 8 → … と値が変わっていきます。
 
このように変換を繰り返したときに、今までに出た値が再度現れるまでの変換回数を G(n, k) と定義します。
 
例えば G(10, 1)＝5 です。5 回目の変換で 3 の値が再度現れていることが分かります（上の太字部分）。
同様に、G(10, 6)＝4, G(10, 0)＝1, G(10, 5)＝3, G(20, 6)＝8 となることが確かめられます。
 
0 以上 n 以下の全ての整数 k に対する G(n, k) の和を H(n) と定義します。
 
例えば H(10)＝42, H(20)＝91, H(100)＝1118 となることが確かめられます。
 
標準入力から、自然数 n（1 ≦ n ≦ 3×105）が与えられます。
標準出力に H(n) の値を出力するプログラムを書いてください。
 
=============================================================================

R で簡素に書くと以下の通り。しかし，実行時間は掛かる。

f = function(n, x) {
    floor(4*x*(n-x)/n)
}

g = function(n, k) {
    nxt = pool = k
    count = 0
    repeat {
        nxt = f(n, nxt)
        count = count+1
        if (nxt %in% pool) {
            return(count)
        }
        pool = c(pool, nxt)
    }
}

h = function(n) {
    sum = 0
    for (k in 0:n) {
        sum = sum+g(n, k)
    }
    sum
}

h(35) # 226
h(350) # 8877
h(1908) # 99344
h(61922) # 8504585
h(99999) # 35499513
h(299997) # 204796803

> h(35) # 226
[1] 226
> h(350) # 8877
[1] 8877
> h(1908) # 99344
[1] 99344

Java や C++ で，いくつものこそくな手段を弄して書いても，h(299997) には，手元のパソコンでも 1.5 sec. ほど掛かってしまうのだ。

import java.util.Scanner;

public class Main {

    public static void main(String[] args) {
        if (false) {
            Scanner cin = new Scanner(System.in);
            String line;
            line = cin.nextLine();
            int n = Integer.parseInt(line);
            h(n);
        } else {
             long start = System.currentTimeMillis();
            // h(35); // 226
            //h(350); // 8877
            // h(1908); // 99344
            // h(61922); // 8504585
            // h(99999); // 35499513
            // h(299997); // 204796803
             long end = System.currentTimeMillis();
             System.out.println((end - start) + "ms");
        }
    }

    static void h(int n) {
        boolean[] exists = new boolean[n + 1];
        double n4 = 4.0 / n;
        int sum = 0;
        int[] suf = new int[n + 1];
        for (int k = 0; n >= k; k++) {
            int next;
            next = k;
            exists[next] = true;
            int c = 0;
            suf[c++] = next;
            int count = 0;
            for (;;) {
                next = (int) (n4 * next * (n - next));
                count++;
                if (exists[next]) {
                    sum += count;
                    break;
                }
                exists[next] = true;
                suf[c++] = next;
            }
            for (int i = 0; i < c; i++) {
                exists[suf[i]] = false;
            }
        }
        System.out.println(sum);
    }

}