算額（その5）

算額（その5）

四十一 群馬県高崎市下小鳥町 幸宮神社 文政7年(1824)
群馬県和算研究会:群馬の算額，上武印刷株式会社，高崎市，1987年3月31日.

群馬県高崎市 幸宮神社 文政7年(1824)
https://blog.goo.ne.jp/r-de-r/e/95e0d587bc8ce1d15512697ad8ad6102

キーワード：円4個，外円，正六角形3個
#Julia, #SymPy, #算額, #和算

東京都府中市の大国魂神社にも同じ問題（上下が反対）の算額があるが，それは明治 18 年(1885) のものだ。

大円に接する 3 個の正六角形と，大円および正六角形に接する 3 個の円がある。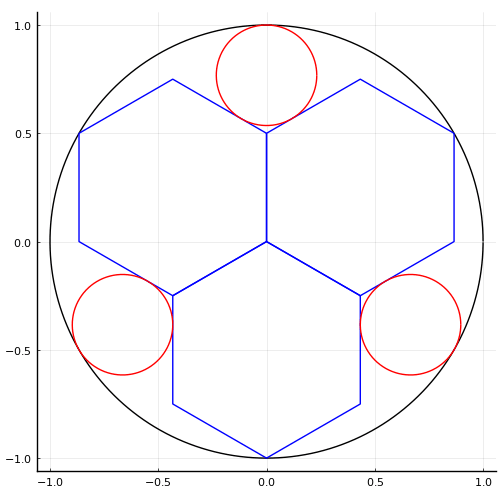

大円，小円の半径をそれぞれ r, x とする。x を求めよ。

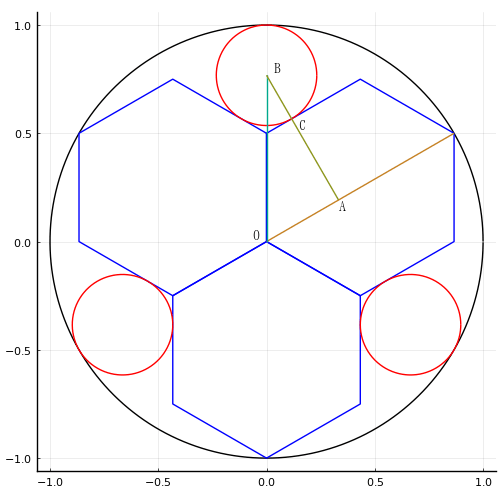
AB = AC + CB = √3/4 \* r + x，OB = r - x とすると，AB / OB = cos(π/6) である。

using SymPy
@syms r::positive, x::positive;

eq1 = (r*sqrt(Sym(3))/4+x) / (r - x) - cos(PI/6);
res = solve(eq1, x);
res[1] |> factor |> println

   r*(-3 + 2*sqrt(3))/2

小円の半径は x = r*(2*√3 - 3)/2 である。

include("julia-source.txt");

function hexagon(ox, oy, ol; color=:blue)
   θ = range(pi/6, pi*13/6, length=7)
   sinθ = ol.*sin.(θ).+oy
   cosθ = ol.*cos.(θ).+ox
   plot!(cosθ, sinθ, color=color, lw=0.5)
end;

function draw(r=1, more=true)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
    pi6 = pi/6
    plot()
    circle2(0, 0, r, :black)
    hexagon(0.5r*cos(pi6), 0.5r*sin(pi6), 0.5r)
    hexagon(0.5r*cos(pi6+4pi6), 0.5r*sin(pi6+4pi6), 0.5r)
    hexagon(0.5r*cos(pi6+8pi6), 0.5r*sin(pi6+8pi6), 0.5r)
    x = (2*sqrt(3) - 3)r/2
    circle2(0, r-x, x)
    circle2((r-x)*cos(7*pi6), (r-x)*sin(7*pi6), x)
    circle2((r-x)*cos(11*pi6), (r-x)*sin(11*pi6), x)
    if more
        delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
        hline!([0], color=:gray80, lw=0.5)
        vline!([0], color=:gray80, lw=0.5)
        plot!([0, r*cos(pi6)], [0, r*sin(pi6)])
        plot!([0, 0], [0, r-x])
        plot!([0, (r-x)/2*cos(pi6)], [r-x, (r-x)/2*sin(pi6)])
        annotate!(0, 0, text("O ", 10, :right, :bottom))
        annotate!((r-x)/2*cos(pi6), (r-x)/2*sin(pi6), text("A", 10, :left, :top))
        annotate!(0, r-x, text(" B", 10, :left, :bottom))
        annotate!(x*sin(pi6), r-(x+x*cos(pi6)), text(" C", 10, :left, :top))
    end
end

draw(1, true)

算額（その4）

算額（その4）

大阪府茨木市 総持寺 嘉永7(1854)年3月
http://www.wasan.jp/osaka/sojiji.html

大阪府茨木市 総持寺 嘉永7(1854)年3月
近畿数学史学会：近畿の算額「数学の絵馬を訪ねて」，平成4年5月16日 初版第一刷，大阪教育図書株式会社，大阪市.

(3) 奈良県大和郡山市小泉町 耳成山口神社 嘉永7年(1854)
近畿数学史学会：近畿の算額「数学の絵馬を訪ねて」，平成4年5月16日 初版第一刷，大阪教育図書株式会社，大阪市.

香川県三豊市豊中町本山 本山寺 万延元年(1860)
http://www.wasan.jp/kagawa/honzanji2.html

六八 川越市石田 藤宮神社 明治4年(1871)
埼玉県立図書館：埼玉県史料集 第二集『埼玉の算額』，昭和44年，誠美堂印刷所，埼玉県与野市.

正三角形の底辺に内接し，隣同士の円も接する3つの円が，更に頂点を通る1つの円とも接するような場合，大円，中円，小円の半径を求めよ。

正三角形の一辺の長さを 2 とし，大円，中円，小円の半径を r1, r2, r3 とし，中円の中心座標を (x2, r2) とする。

using SymPy
@syms r1::positive, r2::positive, r3::positive;
x2 = 1 - √Sym(3)r2;
eq1 = (r2 - r3)^2 + x2^2 - (r2 + r3)^2;
eq2 = 2r1 + 2r3 - √Sym(3);
eq3 = (√Sym(3) - r1 - r2)^2 + x2^2 - (r1 + r2)^2;
res = solve([eq1, eq2, eq3])

   2-element Vector{Dict{Any, Any}}:
    Dict(r2 => sqrt(3), r3 => sqrt(3)/3, r1 => sqrt(3)/6)
    Dict(r2 => sqrt(3)/6, r3 => sqrt(3)/8, r1 => 3*sqrt(3)/8)

r1 > r2 > r3 なので，Dict(r3 => sqrt(3)/3, r2 => sqrt(3), r1 => sqrt(3)/6) は不適切である。

res[1][r1].evalf(), res[1][r2].evalf(), res[1][r3].evalf()

   (0.288675134594813, 1.73205080756888, 0.577350269189626)

Dict(r3 => sqrt(3)/8, r2 => sqrt(3)/6, r1 => 3*sqrt(3)/8) が適切な解である。

res[2][r1].evalf(), res[2][r2].evalf(), res[2][r3].evalf()

   (0.649519052838329, 0.288675134594813, 0.216506350946110)

なお，x2 = 1-√3 r2 = 1-√3 (√3/6) = 0.5 である。

---

using Plots

function circle2(ox, oy, r; color=:red)
   theta = 0:0.01:2pi
   x = r.*cos.(theta)
   y = r.*sin.(theta)
   plot!(ox .+ x, oy .+ y, color=color)
end;

function draw(more)
   sqrt3 = sqrt(3)
   r3 = sqrt3/8
   r2 = sqrt3/6
   r1 = 3sqrt3/8
   println("r1 = $r1,  r2 = $r2,  r3 = $r3")
   x2 = 1-sqrt3*r2  # 0.5
   pyplot(size=(500, 500), aspectratio=1, label="", fontfamily="IPAMincho")
   plot([-1, 1, 0, -1], [0, 0, sqrt3, 0])
   circle2(0, sqrt3-r1, r1)
   circle2(0, r3, r3)
   circle2(x2, r2, r2)
   circle2(-x2, r2, r2)
   if more == true
       scatter!([0, x2, 0, -1+sqrt3*r2], [sqrt3-r1, r2, r3, r2])
       plot!([0, 0], [sqrt3-r1, sqrt3])
       annotate!(0, sqrt3-r1/2, text(" r1", 10, :left))
       plot!([x2, x2], [r2, 0])
       annotate!(x2, r2/2, text(" r2", 10, :left))
       annotate!(x2, 1.2*r2, text("(x2,r2)", 10))
       plot!([-x2, -x2], [r2, 0])
       annotate!(-x2, r2/2, text(" r2", 10, :left))
       plot!([0, 0], [r3, 0])
       annotate!(0, r3/2, text(" r3", 10, :left))
   end
end
draw(true)
   r1 = 3sqrt3/8,  r2 = sqrt3/6,  r3 = sqrt3/8