45 ページの図。こんな図は派手だけど,困るなあ。
死亡者の数値を描いてある位置も恣意的だし。
二軸のグラフは二軸目の目盛りをどのように目盛るかでも印象が変わったりするし。
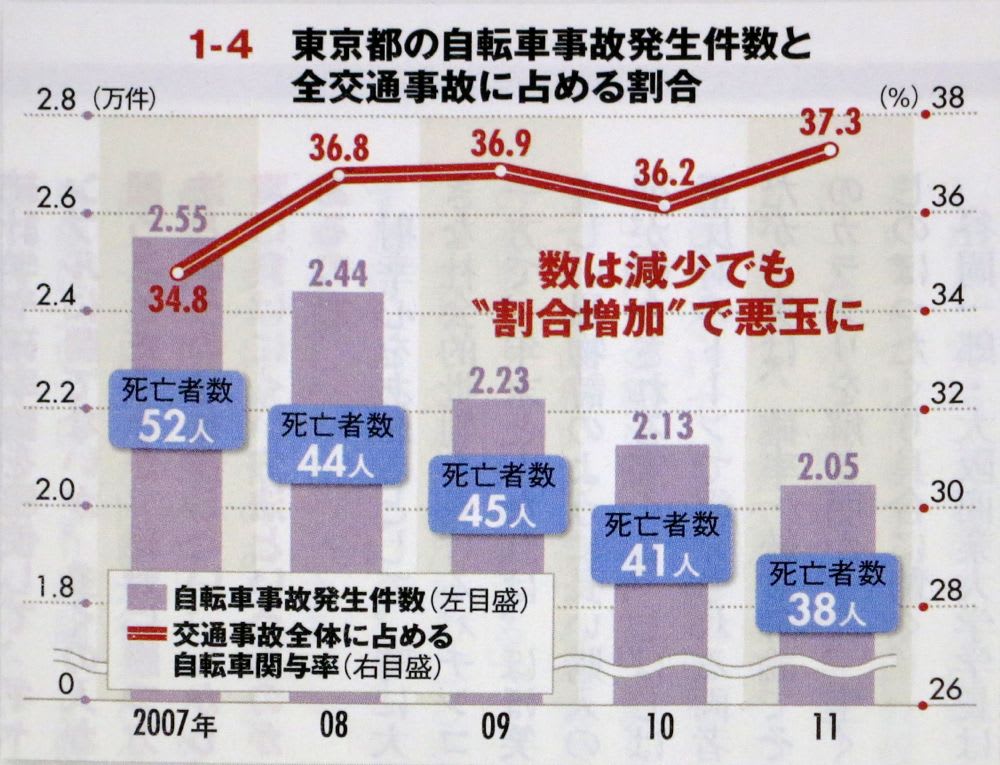
原点から始めてもらわないと。

統計!,統計!!というなら,ちゃんとやろうよね。
45 ページの図。こんな図は派手だけど,困るなあ。
死亡者の数値を描いてある位置も恣意的だし。
二軸のグラフは二軸目の目盛りをどのように目盛るかでも印象が変わったりするし。

原点から始めてもらわないと。

統計!,統計!!というなら,ちゃんとやろうよね。
標準誤差
標準偏差(SD)とは,平均値に対する観測データのばらつきを表すが,標準誤差(SE)は,母集団の散らばりを表す。
---------
標準誤差についての説明は,全くのでたらめです。
標準誤差とは「母集団から標本を抽出し,標本(データ)の集計によって得られる統計量(標本平均とか,標本比率とかなんでも)のバラツキを表すもの。標本統計量の標準偏差を特に標準誤差という。例えば,標本平均の標準誤差は,「母分散/サンプルサイズ」の平方根である。」
対談者が「サンプリングの話でいうと,先ほど平均値と中央値の話をしましたが,『標準誤差』を一緒に把握しておく必要があります。平均点70点で標準誤差20点の人と,平均70点で標準誤差がほぼゼロという人ではまったく異なる人です。ただ,統計学を知らない人に説明する場合,標準誤差になるといきなり理解度が下がりますね。」と語っているのだが,そっくりそのままノシを付けてお返し申し上げたい。対談者がいっているのは,同じ能力を持つ人でも,発揮される能力にバラツキの大きい人と小さい人がいるというのだから,そのバラツキは,標準偏差のことである。
標準誤差が何の役に立つかと言えば,例えば,標本平均は母平均の推定値として使える(標本平均≒母平均)わけだけど,計算される標本平均は実際に母集団から抽出されるデータによって変わるし,データの大きさ(サンプルサイズ)によっても精度は変わる。
標本について言えば,母集団が正規分布に従うならば,標本平均±2×標本標準偏差の範囲には,標本のほぼ 95% が含まれることになる。
これと同じで,標本を抽出し標本平均を計算し,その標本平均を記録する。これを数万回繰り返し,その数万個の標本平均をデータと見なして標準偏差を計算するとその標準偏差が標準誤差にほぼ等しくなるだろう。そして,標本平均±2×標準誤差の範囲には95%くらいの標本平均が含まれるだろう。この区間を,母平均の信頼区間という。母平均の信頼区間は,このようなこと(標本抽出をして,標本に基づいて信頼区間を計算する)を繰り返すと,100回のうちほぼ95回は計算された信頼区間に母平均が含まれるということである。
標本平均で母平均を推定するのが点推定。
母平均を区間で推定するのが区間推定。
これと同じ考え方で,「標本統計量/標準誤差」の大きさで母数についての推測を行うのが,検定。
具体例
母平均値=0,母分散=1の正規分布に従う無限母集団から,標本の大きさ(サンプルサイズ)が 20 の標本を抽出する。標本平均を計算する。
これを,1000000 回行い,1000000 個の標本平均の平均値と標準偏差を求める。
> # このブログの都合で,代入記号に = を使う。よい子はまねしない。
> Means = colMeans(matrix(rnorm(20*1000000), 20))
> (m = mean(Means)) # 0 に近い値のはず
[1] -4.836502e-05
> (s = sd(Means)) # 1/sqrt(20) ≒ 0.2236068 に近い値のはず
[1] 0.2235299
> mean(Means = m+2*s) # 0.05 に近い値のはず
[1] 0.045334
クロス集計
与えられたデータのうち,複数の項目を掛け合わせてデータ分析を行うこと。クロスさせるデータに上限はないが,増えすぎるとサンプル数が減ってしまう。
-----
クロス集計というのは文字通り「集計」で,まだ「分析」までは行かないだろう。
「複数の項目を掛け合わせて」というのは,複数の変数を対象にして(クロスさせて)ということだろう。前に述べた「分割表」を一般的には「クロス集計表」と呼ぶ人が多い。
一番簡単なのは,二重クロス集計。二次元の度数分布表を作るということ。前に述べた,四分表は更に単純な場合(2行2列しかない)。行方向に一方の変数のカテゴリー(カテゴリー変数でない連続変数の場合はカテゴリー化して使用),列方向にもう一方の変数のカテゴリーをとり,それぞれのカテゴリーに該当するデータ数を数え,セルに記入する。期待値や行方向・列方向のパーセントを付けたりもする。
Excel のピボット関数(?)でも集計できるだろう。
 二重クロス表の例
二重クロス表の例
 三重クロス表の例
三重クロス表の例
「クロスさせるデータに上限はない」というのは,「クロスさせる変数の個数に上限はない」ということだろうか。3変数について3重クロスをすれば,3次元の度数分布表になるが,まあ,紙に印刷して提示するためには,二次元にして表示することになる。以下,n変数についてのn重クロスも同じことである。
あるいは,次とも関連するが,変数のカテゴリー数のことか?もともとカテゴリー数がほどほどのカテゴリー変数ならよいが,連続変数をカテゴリー化してクロス集計を使用として,階級幅を狭くする(結果として,カテゴリー数が大きくなる)とか,そもそもカテゴリー数が大きいと,集計結果が入る延べのセルの数が大きくなるので,必然的にセルあたりのデータ数が少なくなるというような,次の項のようなことが生じる。
「上限はないが,増えすぎるとサンプル数が減ってしまう」これは,集計表のセルに該当するデータの個数が少なくなってしまうということ。
「サンプル数」という言葉も微妙。