「ロンリー・ルーク」問題
締め切りが 2017/05/18 10:00 AM なので,その 1 分後に投稿されるように予約
設問
自然数 n, k に対し、縦横 n×n のマス目にチェスのルークの駒を k 個配置することを考えます。
このとき、自身から見て上下方向・左右方向のいずれにも他の駒が存在しないような駒を「はぐれルーク」と呼びます。
例えば以下は、(n, k)=(4, 5) のときの駒の配置例を示しています。
それぞれ、はぐれルークを灰色丸、そうでないルークを青色丸で示しています。
また、はぐれルークの個数は、左図では 1 個、右図では 2 個であることが分かります。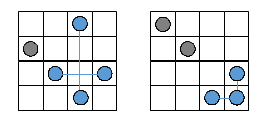
さて、1 つのマスに 2 個以上の駒を置かないよう、ランダムに駒を配置します。
このとき、はぐれルークの個数の期待値を F(n, k) と定義します。
例えば F(2, 2)=2/3 です。
可能な駒の配置は以下の 6 通りです。このうち真ん中の 2 通りでのはぐれルークの個数は 2 個で、他の 4 通りでは 0 個です。
したがって期待値は、0×(4/6)+2×(2/6) = 2/3 となります。
同様に、F(2, 1)=1, F(4, 2)=1.2, F(3, 3)=0.642…, F(4, 5)=0.461…, F(4, 11)=0 となることが確かめられます。
さらに、自然数 n, m に対し、1 ≦ k ≦ m の範囲の自然数 k に対する F(n, k) の和を G(n, m) と定義します。
例えば、G(2, 2)=5/3, G(4, 3)=3.228…, G(4, 5)=4.428… となることが確かめられます。
また、10^3×G(n, m) の整数部分を H(n, m) と定義します。
例えば、H(2, 2)=1666, H(4, 3)=3228, H(4, 5)=4428 です。
標準入力から、自然数 n と m (1 ≦ n ≦ 4, 1 ≦ m ≦ n^2)が半角空白区切りで与えられます。
標準出力に H(n, m) の値を出力するプログラムを書いてください。
なお全てのテストケースにおいて、10^3×G(n, m) の値と、最も近い整数値との差の絶対値は 10^(-3) 以上であることが保証されています。
===================================================
R で簡単に書けるが,計算時間は数秒かかる。
bincombinations = function(p) { # library(e1071) にある
retval = matrix(0, nrow = 2^p, ncol = p)
for (n in 1:p) {
retval[, n] = rep(c(rep(0, (2^p/2^n)), rep(1, (2^p/2^n))),
length = 2^p)
}
retval
}
f = function(n, m) {
check = function(x) {
rSum = rowSums(x) == 1
cSum = colSums(x) == 1
sum(outer(rSum, cSum, "&") & x)
}
len = 2^(n*n)
a = array(t(bincombinations(n*n)), dim=c(n, n, len))
s = apply(a, 3, sum)
sm = apply(a, 3, check)
tbl = table(s, sm)
rSum = rowSums(tbl)
F = colSums(t(tbl / rSum) * 0:n)
G = cumsum(F)
ans = G[m+1]
H = floor(ans*1000)
cat(H)
}
# s = scan(file("stdin", "r"))
# f(s[1], s[2])
#f(2, 3) # 1666
#f(3, 3) # 2642
#f(3, 4) # 2928
#f(4, 4) # 3967
#f(4, 7) # 4797
#f(4, 16) # 4857, 2.922 seq.
Java で書けば,計算は一瞬で終わるが,プログラムを書くのが面倒だ。
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
if (true) {
System.out.println(f(2, 3)); // 1666
System.out.println(f(3, 3)); // 2642
System.out.println(f(3, 4)); // 2928
System.out.println(f(4, 4)); // 3967
System.out.println(f(4, 7)); // 4797
System.out.println(f(4, 16)); // 4857
} else {
Scanner cin = new Scanner(System.in);
String line;
String[] line2 = new String[2];
line = cin.nextLine();
line2 = line.split(" ");
int n = Integer.parseInt(line2[0]);
int m = Integer.parseInt(line2[1]);
System.out.println(f(n, m));
}
}
static int pow2(int n) {
int i, res = 1;
for (i = 0; i < n; i++) {
res *= 2;
}
return res;
}
static int check(int[][] subMat, int n) {
int i, j;
int [] rowSums = new int[n];
int [] colSums = new int[n];
for (i = 0; i < n; i++) {
for (j = 0; j < n; j++) {
rowSums[i] += subMat[i][j];
colSums[j] += subMat[i][j];
}
}
int sum = 0;
for (i = 0; i < n; i++) {
for (j = 0; j < n; j++) {
if (subMat[i][j] == 1 && rowSums[i] == 1 && colSums[j] == 1) {
sum++;
}
}
}
return sum;
}
static int f(int n, int m) {
int i, j, k;
int[][] ary = bincombinations(n * n);
int[][] subMat = new int[n][n];
double[][] tbl = new double[n * n + 1][n + 1];
for (i = 0; i < pow2(n * n); i++) {
int s = 0;
for (j = 0; j < n * n; j++) {
s += ary[i][j];
}
for (j = 0; j < n; j++) {
for (k = 0; k < n; k++) {
subMat[j][k] = ary[i][j * n + k];
}
}
tbl[s][check(subMat, n)]++;
}
double ans = 0;
for (i = 0; m >= i; i++) {
int rSum = 0;
for (j = 0; j < n + 1; j++) {
rSum += tbl[i][j];
}
for (j = 0; j < n + 1; j++) {
tbl[i][j] /= rSum;
ans += tbl[i][j] * j;
}
}
return (int) (ans * 1000);
}
static int[] c(int[] x, int[] y) {
int lenX = x.length;
int lenY = y.length;
int i;
int[] res = new int[lenX + lenY];
for (i = 0; i < lenX; i++) {
res[i] = x[i];
}
for (i = 0; i < lenY; i++) {
res[lenX + i] = y[i];
}
return res;
}
static int[] rep(int[] x, int len) {
int i, pos = 0;
int[] res = new int[len];
int m = x.length;
for (;;) {
for (i = 0; i < m; i++) {
res[pos++] = x[i];
if (pos == len) {
return res;
}
}
}
}
static int[][] bincombinations(int p) {
int[] zero = { 0 };
int[] one = { 1 };
int m = pow2(p);
int[][] ary = new int[m][p];
int[] x = new int[m];
int n, i;
for (n = 0; n < p; n++) {
x = rep(c(rep(zero, pow2(p - n - 1)), rep(one, pow2(p - n - 1))), pow2(p));
for (i = 0; i < m; i++) {
ary[i][n] = x[i];
}
}
return ary;
}
}


















