算額（その17）

算額（その17）

円の内部に大きい円が 6 個，小さい円が 3 個ある。それぞれの円の半径を求めよ。

千葉県木更津市 高柳不動
http://www.wasan.jp/chiba/takayanagi.html

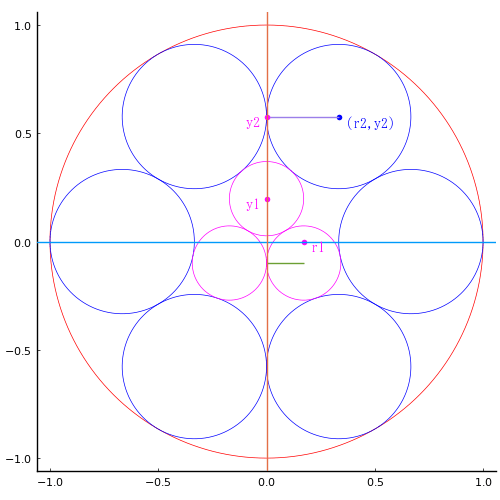
右上の大きな円の半径と中心座標を r2, (r2, y2) とする。
一番上の小さな円の半径と中心座標を r1, (0, y1) とする。

using SymPy

@syms r1::positive, y1::positive, r2::positive, y2::positive;

r2, y2 は方程式を立てなくてもわかるが一応形式的に。

eq1 = y2 - (1 - r2)*sind(Sym(60));
eq2 = r2 - (1 - r2)*cosd(Sym(60));

先の円と接する小さな塩の関係から以下の式を得る。

eq3 = (y2 - y1)^2 + r2^2 - (r1 + r2)^2;

一番上にある小さな円の半径を 1，中心座標を (0, y1) とすると，

eq4 = y1 * sind(Sym(60)) - r1;

方程式を解き，解を求める。

res = solve([eq1, eq2, eq3, eq4], (r1, y1, r2, y2))

   2-element Vector{NTuple{4, Sym}}:
    (3 - 2*sqrt(2), -4*sqrt(6)/3 + 2*sqrt(3), 1/3, sqrt(3)/3)
    (2*sqrt(2) + 3, 4*sqrt(6)/3 + 2*sqrt(3), 1/3, sqrt(3)/3)

r1 = 2*sqrt(2) + 3 は外円より大きいので不適切解である。

回答：

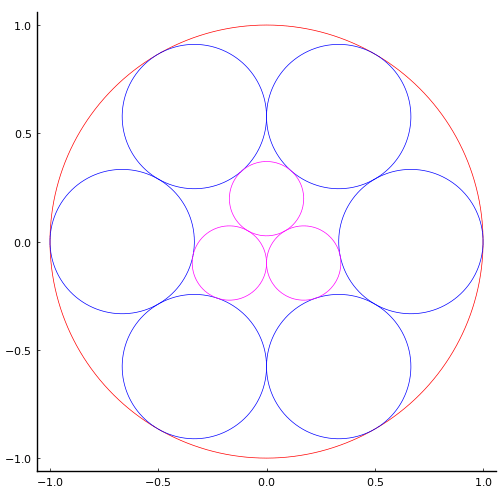
大きな円の半径 1/3
小さな円の半径 3 - 2√2

using Plots

function circle(ox, oy, r, color=:red; beginangle=0, endangle=360)
   θ = beginangle:0.1:endangle
   x = r.*cosd.(θ)
   y = r.*sind.(θ)
   plot!(ox .+ x, oy .+ y, color=color, linewidth=0.5)
end;

function point(x, y, string="", color=:green, position=:left, vertical=:top)
   scatter!([x], [y], color=color, markerstrokewidth=0)
   annotate!(x, y, text(string, 10, position, color, vertical))
end;

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r1, y1, r2, y2) = (3 - 2*sqrt(2), -4*sqrt(6)/3 + 2*sqrt(3), 1/3, sqrt(3)/3)
   println("r1 = $r1,  y1 = $y1,  r2 = $r2,  y2 = $y2")
   plot()
   circle(0, 0, 1)
   circle(r2, y2, r2, :blue)
   circle(-r2, y2, r2, :blue)
   circle(r2, -y2, r2, :blue)
   circle(-r2, -y2, r2, :blue)
   circle(1-r2, 0, r2, :blue)
   circle(r2-1, 0, r2, :blue)
   circle(0, y1, r1, :magenta)
   circle(r1, y1 - 2r1*sind(60), r1, :magenta)
   circle(-r1, y1 - 2r1*sind(60), r1, :magenta)
   if more
       point(r2, y2, " (r2,y2)", :blue)
       plot!([0, r2], [y2, y2])
       point(0, y2, "y2 ", :magenta, :right)
       point(0, y1, "y1 ", :magenta, :right)
       point(r1, 0, " r1", :magenta, :left, :top)
       plot!([0, r1], [y1 - 2r1*sind(60), y1 - 2r1*sind(60)])
       hline!([0])
       vline!([0])
   end
end;

 

算額（その16）

算額（その16）

図のように円が十字に仕切られており，内部に 4 つの円がある。大きい順に甲円，乙円，丙円，丁円とする。乙円，丙円，丁円の径はそれぞれ 4 寸，3 寸，2 寸である。甲円の径はいくつか。

福島県福島市上湯町 薬師堂
http://www.wasan.jp/fukusima/kamiyuyakusi.html

「甲径は 8 寸 4 分である」としているが，もう少し正確には 8.4748 寸（図にすると，外接円との間に隙間がある）。

• 十字の仕切り線の好転を原点とする。
• 甲円の半径を r とすれば，中心座標は (r, -r) である。
• 外円の半径と中心座標を R, (x, y) とする。

以下のように方程式を立て，それを解く。

using SymPy

@syms x::positive, y::negative, r::positive, R::positive;

eq1 = (-4 - x)^2 + (-4 - y)^2 - (R - 4)^2;
eq2 = ( 3 - x)^2 + ( 3 - y)^2 - (R - 3)^2;
eq3 = (-2 - x)^2 + ( 2 - y)^2 - (R - 2)^2;
eq4 = ( r - x)^2 + (-r - y)^2 - (R - r)^2;

res = solve([eq1, eq2, eq3, eq4], (r, x, y, R))

   1-element Vector{NTuple{4, Sym}}:
    (-5*sqrt(97)/24 + 3/8 + sqrt(2)*sqrt(1395*sqrt(97) + 15941)/24, 5*sqrt(97)/24 + 19/8, -59/16 - 5*sqrt(97)/16, 91/16 + 35*sqrt(97)/48)

rem = ["r", "x", "y", "R"]
for i in 1:4
   println("$(rem[i]) = $(res[1][i].evalf())")
   println(res[1][i], "\n")
end

   r = 8.47480963363268
   -5*sqrt(97)/24 + 3/8 + sqrt(2)*sqrt(1395*sqrt(97) + 15941)/24

   x = 4.42684537537419
   5*sqrt(97)/24 + 19/8

   y = -6.76526806306128
   -59/16 - 5*sqrt(97)/16

   R = 12.8689588138097
   91/16 + 35*sqrt(97)/48

r を取り出すのは res[1][1]。sympy.sqrtdenest で二重根号を外してから expand すると簡単な式になる。

res[1][1] |> sympy.sqrtdenest |> expand |> println

   sqrt(97)/6 + 41/6

(41 + √97) / 6

   8.474809633632683

using Plots

function circle(ox, oy, r, color=:red; beginangle=0, endangle=360)
   θ = beginangle:0.1:endangle
   x = r.*cosd.(θ)
   y = r.*sind.(θ)
   plot!(ox .+ x, oy .+ y, color=color, linewidth=0.5)
end;

function point(x, y, string="", color=:green, position=:left, vertical=:top)
   scatter!([x], [y], color=color, markerstrokewidth=0)
   annotate!(x, y, text(string, 10, position, color, vertical))
end;

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (x, y, r, R) = (5*sqrt(97)/24 + 19/8,
                   -59/16 - 5*sqrt(97)/16,
                   -5*sqrt(97)/24 + 3/8 + sqrt(2)*sqrt(1395*sqrt(97) + 15941)/24,
                   91/16 + 35*sqrt(97)/48)
   println("rx = $x,  y = $y,  r = $r,  R = $R")
   plot()
   circle(-4, -4, 4, :blue)
   circle( 3,  3, 3, :blue)
   circle(-2,  2, 2, :blue)
   circle( r, -r, r, :blue)
   circle( x,  y, R, :green)
   if more
       point(-4, -4, " 乙", :blue)
       point( 3,  3, " 丙", :blue)
       point(-2,  2, " 丁", :blue)
       point( r, -r, " 甲(r,-r)", :blue)
       point( x,  y, " 外円(x,y)", :green)
   end
   hline!([0])
   vline!([0])
end;