算額（その38）

算額（その38）

新潟県糸魚川市 天津神社 寛政12年
http://www.wasan.jp/niigata/tensin.html

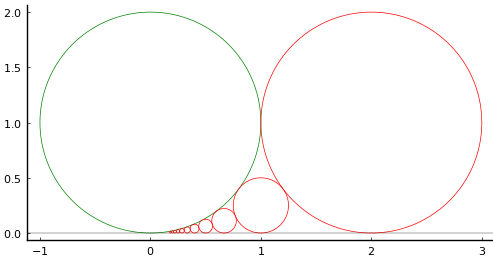
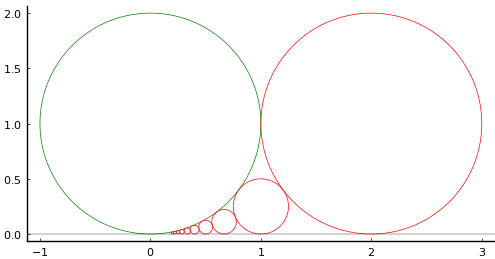
図のように，外円の中に 5 種類の径（木，火，土，金，水）を持つ円が収まっている。土円，金円の径はそれぞれ 9分9釐（厘），一寸9分9釐（厘）である。水円の径を求めよ。

図のように記号を定め，方程式を解く。水円の径は r3 である。（プログラムでは，すべて直径ではなく半径を使っている。）

using SymPy
@syms　r1::positive, r2::positive, y2::positive, r0::positive, y3::positive, r3::positive, r4::positive, x4::positive, y4::positive, r5::positive, x5::positive, y5::positive;

r1 = 99
r2 = 198
y3 = r3
x5 = r5
x4 = r4
eq1 = x4^2+(2r0-r1-y4)^2-(r1+r4)^2
eq2 = x4^2+(y4-y2)^2-(r2+r4)^2
eq3 = x5^2+(y2-y5)^2-(r2+r5)^2
eq4 = x5^2+(y5-y3)^2-(r3+r5)^2
eq5 = x4^2+(y4-r0)^2-(r0-r4)^2b
eq6 = x5^2+(r0-y5)^2-(r0-r5)^2
eq7 = (x5 - x4)^2 + (y4 - y5)^2 - (r4 + r5)^2;

# res = solve([eq1, eq2, eq3, eq4, eq5, eq6, eq7], (y2, r0, r3, r4, y4, r5, y5))

solve() では解が求まらないので，nlsolve() で求める。

using NLsolve

function nls(func, params...; ini = [0.0])
 if typeof(ini) <: Number
    r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params...), [ini], ftol=1e-14)
    v = r.zero[1]
 else
    r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=1e-14)
    v = r.zero
 end
 return v, r.f_converged
end;

function h(u)
   y2, r0, r3, r4, y4, r5, y5 = u
   return [
       r4^2 - (r4 + 99)^2 + (2*r0 - y4 - 99)^2
       r4^2 - (r4 + 198)^2 + (-y2 + y4)^2
       r5^2 - (r5 + 198)^2 + (y2 - y5)^2
       r5^2 + (-r3 + y5)^2 - (r3 + r5)^2
       r4^2 + (-r0 + y4)^2 - (r0 - r4)^2
       r5^2 - (r0 - r5)^2 + (r0 - y5)^2
       (-r4 + r5)^2 - (r4 + r5)^2 + (y4 - y5)^2
 ];
end;

iniv = [2260., 1521, 580, 326, 2670, 752, 1679];

res = nls(h, ini=iniv)

y2, r0, r3, r4, y4, r5, y5 = res[1]

   7-element Vector{Float64}:
    2260.2616848711004
    1521.243310737389
     580.0010348927411
     326.36779179808775
    2670.68298737871
     752.3774162147455
    1679.6194053038619

求める水円の径は 580.0010348927411 である。

using Plots

function circle(ox, oy, r, color=:red; beginangle=0, endangle=360)
   θ = beginangle:0.1:endangle
   x = r.*cosd.(θ)
   y = r.*sind.(θ)
   plot!(ox .+ x, oy .+ y, color=color, linewidth=0.5)
end;

function point(x, y, string="", color=:green, position=:left, vertical=:top)
   scatter!([x], [y], color=color, markerstrokewidth=0)
   annotate!(x, y, text(string, 10, position, color, vertical))
end;

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r1 = 99
   r2 = 198
   y2, r0, r3, r4, y4, r5, y5 = [2260.2616848711004, 1521.243310737389, 580.0010348927411, 326.36779179808775, 2670.68298737871, 752.3774162147455, 1679.6194053038619]
   y3 = r3
   x4 = r4
   x5 = r5
   println("r0 = $r0,  r1 = $r1,  r2 = $r2,  r3 = $r3,  r4 = $r4,  r5 = $r5")
   println("y2 = $y2,  y3 = $y3,  x4 = $x4,  y4 = $y4,  x5 = $x5,  y5 = $y5")
   plot()
   circle(0, r0, r0, :green)
   circle(0, 2r0-r1, r1)
   circle(0, y2, r2, :blue)
   circle(0, y3, r3, :brown)
   circle(x4, y4, r4, :magenta)
   circle(-x4, y4, r4, :magenta)
   circle(x5, y5, r5, :black)
   circle(-x5, y5, r5, :black)
   if more
       point(0, r0, "r0 ", :green, :right)
       point(0, 2r0-r1, "r1 ", :red, :right)
       point(0, y2, "y2 ", :blue, :right)
       point(0, y3, "r3 ", :brown, :right)
       point(x4, y4, "(x4,y4)", :magenta, :center)
       point(x5, y5, "(x5,y5)", :black, :center)
       vline!([0], color=:black, linewidth=0.25)
       hline!([0], color=:black, linewidth=0.25)
   end
end;

 

算額（その37）

算額（その37）

新潟県三島郡 与板八幡宮 寛政12年
新潟県柏崎市与板 与板三柱神社 であろう
http://www.wasan.jp/niigata/yoitahatiman1.html

「長」，「平」，「高」の 3 辺を持つ直方体において，

• 「長」，「平」 の差は 1 寸
• 「斜」は 13 寸

直方体の体積が最も大きくなるのは，「長」がいくつのときか。

直方体の底面の対角線を L として，以下の式を立てる。

using SymPy
@syms 長::positive, 平::positive, 高::positive, 斜::positive, L::positive;

斜 = 13
平 = 長 - 1
eq2 = 長^2 + 平^2 - L^2;
eq3 = L^2 + 高^2 - 斜^2;

res = solve([eq2, eq3], (L, 高))

   1-element Vector{Tuple{Sym, Sym}}:
    (sqrt(2*長^2 - 2*長 + 1), sqrt(2)*sqrt(-長^2 + 長 + 84))

volume = 長 * 平 * res[1][2]
volume |> println

   sqrt(2)*長*(長 - 1)*sqrt(-長^2 + 長 + 84)

diff(volume) |> solve |> println

   Sym[1/2, 8]

1/2 は不適切解なので，正解は 8 （寸）である。

ちなみに，高さは

sqrt(2)*sqrt(-長^2 + 長 + 84)(長 => 8).evalf()

   7.48331477354788

 

算額（その36）

算額（その36）

新潟県三島郡 与板八幡宮 寛政12年
新潟県柏崎市与板 与板三柱神社 であろう
http://www.wasan.jp/niigata/yoitahatiman2.html

直線と互いに接する大円と小円があり，更に小円と大円と直線に接する連続する小円がある。大円の径が225寸，一番小さい小円の径が4寸のとき，赤で示した面積が最大になるときの一番大きい小円の径はいくつになるか。

答えを先に述べておく。

算額によれば，径 4 寸から径 100 寸の最大の小円まで全部で 5 個とあるが，本当は 7 個ではないか?

この問題は，算額（その35）の後半に示したプログラムで解くことができる。
大円の半径を R，小さい方から 2 つの小円の半径と中心の x 座標を r1, x1, r2, x2 と置き，以下の方程式を立てる。

using SymPy
@syms R::positive, r1::positive, r2::positive, x1::positive, x2::positive;

R = 225
eq1 = x1^2 + (R - r1)^2 - (R + r1)^2;
eq2 = x2^2 + (R - r2)^2 - (R + r2)^2;
eq3 = (x1 - x2)^2 + (r1 - r2)^2 - (r1 + r2)^2;

solve(eq1, x1) |> println

   Sym[2*sqrt(R)*sqrt(r1)]

res = solve([eq1, eq2, eq3], (r1, x1));
res[2][1] |> simplify |> println
res[2][2] |> simplify |> println

   x2^2*(2*sqrt(R)*sqrt(r2) + R + r2)/(4*(R - r2)^2)
   x2*(sqrt(R)*sqrt(r2) + R)/(R - r2)

SymPy はここまで。JupyterLab などを使っている場合は，ここでカーネルをリスタートする。

次に大きい円を求める関数を定義する。

function nextcircle(r2, x2; R = 225)
   r = x2^2*(2*sqrt(R)*sqrt(r2) + R + r2)/(4*(R - r2)^2)
   x = x2*(sqrt(R)*sqrt(r2) + R)/(R - r2)
   return r, x
end;

この漸化式によれば，半径が 4 寸からスタートして 7 番目の小円の半径がほぼ 100 になることが確認できる。

算額によれば，径 4 寸から径 100 寸の最大の小円まで全部で 5 個とあるが，本当は 7 個ではないか?

R = 225
r = 4 # r1
x = 2*sqrt(R)*sqrt(r) # x1

for i = 2:7
   r, x = nextcircle(r, x, R = 225)
   println("$i, $r, $x")
end

   2, 5.325443786982248, 69.23076923076923
   3, 7.438016528925618, 81.81818181818181
   4, 11.111111111111112, 99.99999999999999
   5, 18.3673469387755, 128.57142857142856
   6, 35.99999999999999, 179.99999999999997
   7, 99.99999999999996, 299.99999999999994

using Plots

function circle(ox, oy, r, color=:red; beginangle=0, endangle=360)
   θ = beginangle:0.1:endangle
   x = r.*cosd.(θ)
   y = r.*sind.(θ)
   plot!(ox .+ x, oy .+ y, color=color, linewidth=0.5)
end;

function point(x, y, string="", color=:green, position=:left, vertical=:top)
   scatter!([x], [y], color=color, markerstrokewidth=0)
   annotate!(x, y, text(string, 10, position, color, vertical))
end;

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   R = 225
   plot()
   circle(0, R, R, :green)
   r = 4 # r1
   x = 2*sqrt(R)*sqrt(r) # x1
   circle(x, r, r)
   println("1, r = $r, x = $x")

   for i = 2:7
       r, x = nextcircle(r, x, R=R)
       println("$i, r = $r, x = $x")
       circle(x, r, r)
   end
   hline!([0], color=:black, linewidth=0.25)
   if more
       point(0, 0, "0 ", :black, :right)
       point(0, r3, "r3 ", :black, :right)
       point(0, r3+r1, "r3+r1 ", :blue, :right)
       point(0, 1-r2, "1-r2 ", :red, :right)
       point(x4, r4, "(x4,r4)", :magenta, :center)
       vline!([0], color=:black, linewidth=0.25)
       hline!([0], color=:black, linewidth=0.25)
   end
end;

draw(false)

   1, r = 4, x = 60.0
   2, r = 5.325443786982248, x = 69.23076923076923
   3, r = 7.438016528925618, x = 81.81818181818181
   4, r = 11.111111111111112, x = 99.99999999999999
   5, r = 18.3673469387755, x = 128.57142857142856
   6, r = 35.99999999999999, x = 179.99999999999997
   7, r = 99.99999999999996, x = 299.99999999999994

 

 

算額（その35）

算額（その35）

新潟県三島郡 与板八幡宮 寛政12年
新潟県柏崎市与板 与板三柱神社 であろう
http://www.wasan.jp/niigata/yoitahatiman1.html

直線と互いに接する大円と小円があり，更に小円と大円と直線に接する連続する小円がある。大円の径が10寸，一番小さい小円の径が1分のとき，小円の数はいくつか。

大円の半径を R，大きい方から 2 つの小円の半径と中心の x 座標を r1, x1, r2, x2 と置き，以下の方程式を立てる。

using SymPy
@syms R::positive, r1::positive, r2::positive, x1::positive, x2::positive;

R = 1
eq1 = x1^2 + (R - r1)^2 - (R + r1)^2;
eq2 = x2^2 + (R - r2)^2 - (R + r2)^2;
eq3 = (x1 - x2)^2 + (r1 - r2)^2 - (r1 + r2)^2;

一番大きい小円の中心の x 座標は，eq1 を x1 について解けば求まる。

solve(eq1, x1)

   2*sqrt(r1)

eq1, eq2, eq3 を r2, x2 について解けば，ある小円の次に小さい小円の半径と中心の x 座標を求める漸化式が得られる。なお，2番めの解は不適切解である。

res = solve([eq1, eq2, eq3], (r2, x2))

   2-element Vector{Tuple{Sym, Sym}}:
    (x1*(-2*sqrt(r1)*x1/(r1 - 1) + x1 + 2*x1/(r1 - 1))/(4*(r1 - 1)), sqrt(r1)*x1/(r1 - 1) - x1/(r1 - 1))
    (x1*(2*sqrt(r1)*x1/(r1 - 1) + x1 + 2*x1/(r1 - 1))/(4*(r1 - 1)), -sqrt(r1)*x1/(r1 - 1) - x1/(r1 - 1))

res[1][1] |> simplify |> println # r2

   x1^2*(-2*sqrt(r1) + r1 + 1)/(4*(r1 - 1)^2)

res[1][2] |> simplify |> println # x2

   x1*(sqrt(r1) - 1)/(r1 - 1)

小円 (r1, x1) から次の小円 (r2, x2) を得る関数を書く。

function nextcircle(r1, x1; R = 1)
   r2 = x1^2*(-2*sqrt(r1) + r1 + 1)/(4*(r1 - 1)^2)
   x2 = x1*(sqrt(r1) - 1)/(r1 - 1)
   return r2, x2
end;

この関数を使い，初期値を 1 にするとエラーになるが，1 に極めて近い値を設定することで 10 番目の小円の半径が大円のほぼ 1/100 = 0.01 になることがわかる。

r = 0.99999 # r1
x = 2sqrt(r) # x1

for i = 2:10
   r, x = nextcircle(r, x)
   println("$i, $r, $x")
end

   2, 0.2499986308990838, 0.999997499986309
   3, 0.11111075838251418, 0.6666656084800361
   4, 0.062499851192534595, 0.499999404769784
   5, 0.03999992381055049, 0.399999619052571
   6, 0.027777733686650655, 0.3333330687864656
   7, 0.020408135499460415, 0.28571409135329967
   8, 0.015624981399050211, 0.24999985119235743
   9, 0.012345665948302833, 0.22222210464580552
   10, 0.009999990476312013, 0.19999990476309745

図示することで，正しく描画されることを確認する。

using Plots

function circle(ox, oy, r, color=:red; beginangle=0, endangle=360)
   θ = beginangle:0.1:endangle
   x = r.*cosd.(θ)
   y = r.*sind.(θ)
   plot!(ox .+ x, oy .+ y, color=color, linewidth=0.5)
end;

function point(x, y, string="", color=:green, position=:left, vertical=:top)
   scatter!([x], [y], color=color, markerstrokewidth=0)
   annotate!(x, y, text(string, 10, position, color, vertical))
end;

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   R = 1
   plot()
   circle(0, R, R, :green)
   r = 0.99999 # r1
   x = 2sqrt(r) # x1
   circle(x, r, r)

   for i = 2:11
       r, x = nextcircle(r, x, R=R)
       println("$i, r = $r, x = $x")
       circle(x, r, r)
   end
   hline!([0], color=:black, linewidth=0.25)
   if more
       point(0, 0, "0 ", :black, :right)
       point(0, r3, "r3 ", :black, :right)
       point(0, r3+r1, "r3+r1 ", :blue, :right)
       point(0, 1-r2, "1-r2 ", :red, :right)
       point(x4, r4, "(x4,r4)", :magenta, :center)
       vline!([0], color=:black, linewidth=0.25)
       hline!([0], color=:black, linewidth=0.25)
   end
end;

draw(false)

   2, r = 0.2499986308990838, x = 0.999997499986309
   3, r = 0.11111075838251418, x = 0.6666656084800361
   4, r = 0.062499851192534595, x = 0.499999404769784
   5, r = 0.03999992381055049, x = 0.399999619052571
   6, r = 0.027777733686650655, x = 0.3333330687864656
   7, r = 0.020408135499460415, x = 0.28571409135329967
   8, r = 0.015624981399050211, x = 0.24999985119235743
   9, r = 0.012345665948302833, x = 0.22222210464580552
   10, r = 0.009999990476312013, x = 0.19999990476309745
   11, r = 0.008264455654629146, x = 0.18181810310999452

-----------
先の方程式を，小円 r2, x2 から次に大きい小円 r1, x1 を求める漸化式を作るように解くと以下のようになる。

using SymPy
@syms R::positive, r1::positive, r2::positive, x1::positive, x2::positive;

R = 1
eq1 = x1^2 + (R - r1)^2 - (R + r1)^2;
eq2 = x2^2 + (R - r2)^2 - (R + r2)^2;
eq3 = (x1 - x2)^2 + (r1 - r2)^2 - (r1 + r2)^2;

solve(eq2, x2)

   2*sqrt(r2)

res = solve([eq1, eq2, eq3], (r1, x1))

   2-element Vector{Tuple{Sym, Sym}}:
    (-x2*(-2*sqrt(r2)*x2/(r2 - 1) - x2 - 2*x2/(r2 - 1))/(4*(r2 - 1)), -sqrt(r2)*x2/(r2 - 1) - x2/(r2 - 1))
    (-x2*(2*sqrt(r2)*x2/(r2 - 1) - x2 - 2*x2/(r2 - 1))/(4*(r2 - 1)), sqrt(r2)*x2/(r2 - 1) - x2/(r2 - 1))

function nextcircle(r2, x2; R = 1)
   r = -x2*(-2*sqrt(r2)*x2/(r2 - 1) - x2 - 2*x2/(r2 - 1))/(4*(r2 - 1))
   x = -sqrt(r2)*x2/(r2 - 1) - x2/(r2 - 1)
   return r, x
end;

この漸化式によれば，半径が 0.01 からスタートして 10 番目の小円の半径がほぼ 1 になることが確認できる。

r = 0.01 # r1
x = 2sqrt(r) # x1

for i = 2:10
   r, x = nextcircle(r, x)
   println("$i, $r, $x")
end

   2, 0.012345679012345682, 0.22222222222222227
   3, 0.01562500000000001, 0.25000000000000006
   4, 0.02040816326530613, 0.28571428571428575
   5, 0.02777777777777779, 0.3333333333333334
   6, 0.04000000000000003, 0.40000000000000013
   7, 0.06250000000000006, 0.5000000000000002
   8, 0.1111111111111112, 0.666666666666667
   9, 0.25000000000000033, 1.0000000000000007
   10, 1.0000000000000027, 2.0000000000000027

using Plots

function circle(ox, oy, r, color=:red; beginangle=0, endangle=360)
   θ = beginangle:0.1:endangle
   x = r.*cosd.(θ)
   y = r.*sind.(θ)
   plot!(ox .+ x, oy .+ y, color=color, linewidth=0.5)
end;

function point(x, y, string="", color=:green, position=:left, vertical=:top)
   scatter!([x], [y], color=color, markerstrokewidth=0)
   annotate!(x, y, text(string, 10, position, color, vertical))
end;

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   R = 1
   plot()
   circle(0, R, R, :green)
   r = 0.01 # r1
   x = 2sqrt(r) # x1
   circle(x, r, r)
   println("1, r = $r, x = $x")

   for i = 2:10
       r, x = nextcircle(r, x, R=R)
       println("$i, r = $r, x = $x")
       circle(x, r, r)
   end
   hline!([0], color=:black, linewidth=0.25)
   if more
       point(0, 0, "0 ", :black, :right)
       point(0, r3, "r3 ", :black, :right)
       point(0, r3+r1, "r3+r1 ", :blue, :right)
       point(0, 1-r2, "1-r2 ", :red, :right)
       point(x4, r4, "(x4,r4)", :magenta, :center)
       vline!([0], color=:black, linewidth=0.25)
       hline!([0], color=:black, linewidth=0.25)
   end
end;

draw(false)

   1, r = 0.01, x = 0.2
   2, r = 0.012345679012345682, x = 0.22222222222222227
   3, r = 0.01562500000000001, x = 0.25000000000000006
   4, r = 0.02040816326530613, x = 0.28571428571428575
   5, r = 0.02777777777777779, x = 0.3333333333333334
   6, r = 0.04000000000000003, x = 0.40000000000000013
   7, r = 0.06250000000000006, x = 0.5000000000000002
   8, r = 0.1111111111111112, x = 0.666666666666667
   9, r = 0.25000000000000033, x = 1.0000000000000007
   10, r = 1.0000000000000027, x = 2.0000000000000027

二番目に小さい小円の半径が 0.012345679012345682 というのは，意味深だなあ。