算額（その193）

算額（その193）

中村信弥「改訂増補 長野県の算額」
http://www.wasan.jp/zoho/zoho.html
県内の算額1（88）
長野県中野市田上 田上観音堂 文化6年(1809)

問2. 大円の中に甲，乙，丙，丁を入れる。それぞれは互いに隣同士の円は外接し，大円に内接する正三角形の底辺及び大円に接している。大円の径が 196 寸，丙円の径が 17寸6分5厘のとき，丁円の径はいかほどか。

大，甲，乙，丙，丁の円の半径を R, r1, r2, r3, r4，それぞれの円の中心座標を (0, 0), (0, -R/2-r1), (x2, -R/2-r2), (x3, -R/2-r3), (x4, -R/2-r4) と置く。ただし，R = 19600, r3 = 1765 とする。

using SymPy

@syms R::positive, r1::positive, x2::positive, r2::positive, x3::positive, r3::positive, x4::positive, r4::positive;

R = 19600
r3 = 1764

eq1 = x2^2 + (r1 - r2)^2 - (r1 + r2)^2
eq2 = (x3 - x2)^2 + (r2 - r3)^2 - (r2 + r3)^2
eq3 = (x4 - x3)^2 + (r3 - r4)^2 - (r3 + r4)^2
eq4 = x2^2 + (R//2 + r2)^2 - (R - r2)^2
eq5 = x3^2 + (R//2 + r3)^2 - (R - r3)^2
eq6 = x4^2 + (R//2 + r4)^2 - (R - r4)^2

res = solve([eq1, eq2, eq3, eq4, eq5, eq6], (r1, r2, r4, x2, x3, x4))

   4-element Vector{NTuple{6, Sym}}:
    (4900, 3675, 675, 4900*sqrt(3), 7840*sqrt(3), 9100*sqrt(3))
    (4900, 3675, 3675, 4900*sqrt(3), 7840*sqrt(3), 4900*sqrt(3))
    (828100/9, 675, 675, 9100*sqrt(3), 7840*sqrt(3), 9100*sqrt(3))
    (828100/9, 675, 3675, 9100*sqrt(3), 7840*sqrt(3), 4900*sqrt(3))

r1 = 4900.00000, r2 = 3675.00000, r4 = 675.00000, x2 = 8487.04896, x3 = 13579.27833, x4 = 15761.66235

r2 > r4 であるから，1 番目の解が適切である。
丙円の半径は r4 = 675，もとの単位でいえば丙円の直径は 6寸7分5厘 である。

using Plots
using Printf

function circle(ox, oy, r, color=:red; beginangle=0, endangle=360)
  θ = beginangle:0.1:endangle
  x = r.*cosd.(θ)
  y = r.*sind.(θ)
  plot!(ox .+ x, oy .+ y, color=color, linewidth=0.5)
end;

function point(x, y, string="", color=:green, position=:left, vertical=:top; mark=true)
   mark && scatter!([x], [y], color=color, markerstrokewidth=0)
   annotate!(x, y, text(string, 10, position, color, vertical))
end;

function draw(more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r1, r2, r4, x2, x3, x4) = res[1]
   @printf("r1 = %.5f, r2 = %.5f, r4 = %.5f, x2 = %.5f, x3 = %.5f, x4 = %.5f\n", r1, r2, r4, x2, x3, x4)
   plot([√3R/2, 0, -√3R/2, √3R/2], [-R/2, R, -R/2, -R/2], color=:blue, lw=0.5)
   circle(0, 0, R, :black)
   circle(0, -R/2 - r1, r1, :blue)
   circle(x2, -R/2 - r2, r2, :green)
   circle(-x2, -R/2 - r2, r2, :green)
   circle(x3, -R/2 - r3, r3, :brown)
   circle(-x3, -R/2 - r3, r3, :brown)
   circle(x4, -R/2 - r4, r4, :red)
   circle(-x4, -R/2 - r4, r4, :red)
   if more == true
       point(0, -R, " -R")
       point(0, -R/2, " -R/2", :green, :left, :bottom) 
       point(0, -R/2-r1, " 甲")
       point(x2, -R/2-r2, " 乙")
       point(x3, -R/2-r3, " 丙")
       point(x4, -R/2-r4, " 丁")
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
   else
      plot!(showaxis=false)
   end
end;

算額（その192）

算額（その192）

中村信弥「改訂増補 長野県の算額」
http://www.wasan.jp/zoho/zoho.html
県内の算額1（88）
長野県中野市田上 田上観音堂 文化6年(1809)

問1. 長方形内に 2 本の斜線を入れ，それぞれに接する甲円と乙円を入れる。長方形の短辺の長さが 10 寸，甲円の直径が 8 寸のとき，長方形の長辺の長さはいかほどか。

長方形の長辺の長さを x，乙円の半径を r，斜線が x 軸，y軸と交わる座標を x1, y1 とする。各円の中心から斜線までの距離が半径に等しいことを条件として，方程式を解く。

using SymPy

function distance(x1, y1, x2, y2, x0, y0)
   p1, p2 = sympy.Point(x1, y1), sympy.Point(x2, y2)
   l = sympy.Line(p1, p2)
   l.distance(sympy.Point(x0, y0))^2  # 二乗距離を返す！！
end;

@syms x::positive, x1::positive, y1::positive, r::positive;

eq1 = distance(0, y1, x, 10, r, r) - r^2 |> simplify
eq2 = distance(0, 10, x1, 0, r, r) - r^2 |> simplify
eq3 = distance(0, y1, x, 10, x - 4, 4) - 4^2 |> simplify
eq4 = distance(0, 10, x1, 0, x - 4, 4) - 4^2 |> simplify

res = solve([eq1, eq2, eq3, eq4], (x, x1, y1, r))

   1-element Vector{NTuple{4, Sym}}:
    (8, 24, 20/3, 4)

今までに経験のないことであるが，solve で得られる解が不適切解である。得られる乙円の半径が 4 という解は甲円と乙円が重なるという解である。

そこで，nlsolve() で解いてみる。

println(eq1, ",")
println(eq2, ",")
println(eq3, ",")
println(eq4, ",")

   x*(2*r^2*y1 - 20*r^2 - 2*r*x*y1 - 2*r*y1^2 + 20*r*y1 + x*y1^2)/(x^2 + y1^2 - 20*y1 + 100),
   20*x1*(r^2 - r*x1 - 10*r + 5*x1)/(x1^2 + 100),
   4*x*(5*x + 12*y1 - 120)/(x^2 + y1^2 - 20*y1 + 100),
   20*(5*x^2 - 6*x*x1 - 40*x + x1^2 + 24*x1)/(x1^2 + 100),

using NLsolve

function nls(func, params...; ini = [0.0])
   if typeof(ini) <: Number
       r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=1e-14)
       v = r.zero[1]
   else
       r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=1e-14)
       v = r.zero
   end
   return v, r.f_converged
end;

function H(u)
   (x, x1, y1, r) = u
   return [
       x*(2*r^2*y1 - 20*r^2 - 2*r*x*y1 - 2*r*y1^2 + 20*r*y1 + x*y1^2)/(x^2 + y1^2 - 20*y1 + 100),
       20*x1*(r^2 - r*x1 - 10*r + 5*x1)/(x1^2 + 100),
       4*x*(5*x + 12*y1 - 120)/(x^2 + y1^2 - 20*y1 + 100),
       20*(5*x^2 - 6*x*x1 - 40*x + x1^2 + 24*x1)/(x1^2 + 100),
   ]
end;

iniv = [big"13.8", 7.8, 4.3, 2.6]
res = nls(H, ini=iniv)
println(res)
   (BigFloat[13.75900072948533162286601728523747073950320887218339386802707109168781010348274, 7.807200583588265253825888517990309019730833318263487969214336156987235887470571, 4.267083029381111827960970371439448927535572362184485605389630903733447101473092, 2.560249817628667040685677767677303452771782038991463293198420137207969259035087], true)

x = 13.75900, x1 = 7.80720, y1 = 4.26708, r = 2.56025
であり，x = 13.75900 は元の単位でいえば 13寸7分5厘9毛 である。算額の答えでは 13寸7分5厘6毛あまりあり となっている。

using Plots
using Printf

function circle(ox, oy, r, color=:red; beginangle=0, endangle=360)
  θ = beginangle:0.1:endangle
  x = r.*cosd.(θ)
  y = r.*sind.(θ)
  plot!(ox .+ x, oy .+ y, color=color, linewidth=0.5)
end;

function point(x, y, string="", color=:green, position=:left, vertical=:top; mark=true)
   mark && scatter!([x], [y], color=color, markerstrokewidth=0)
   annotate!(x, y, text(string, 10, position, color, vertical))
end;

function segment(x1, y1, x2, y2, color=:black; linestyle=:solid, linewidth=0.5)
   plot!([x1, x2], [y1, y2], color=color, linestyle=linestyle, linewidth=linewidth)
end;

function draw(more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (x, x1, y1, r) = res[1]
   @printf("x = %.5f, x1 = %.5f, y1 = %.5f, r = %.5f\n", x, x1, y1, r)
   plot([0, x, x, 0, 0], [0, 0, 10, 10, 0], color=:blue, lw=0.5)
   circle(r, r, r)
   circle(x - 4, 4, 4, :blue)
   segment(0, 10, x1, 0, :green)
   segment(0, y1, x, 10, :green)
   if more == true
       point(x - 4, 4, " 甲: (x-4,4)")
       point(r, r, " 乙: (r,r)")
       point(x1, 0, "x1")
       point(0, y1, "y1 ", :green, :right)
       point(x, 0, " x")
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5, xlims=(-1, 14.5),ylims=(-0.5, 10.5))
   else
      plot!(showaxis=false)
   end
end;

算額（その191）

算額（その191）

中村信弥「改訂増補 長野県の算額」
http://www.wasan.jp/zoho/zoho.html
県内の算額1（88）
長野県中野市田上 田上観音堂 文化6年(1809)

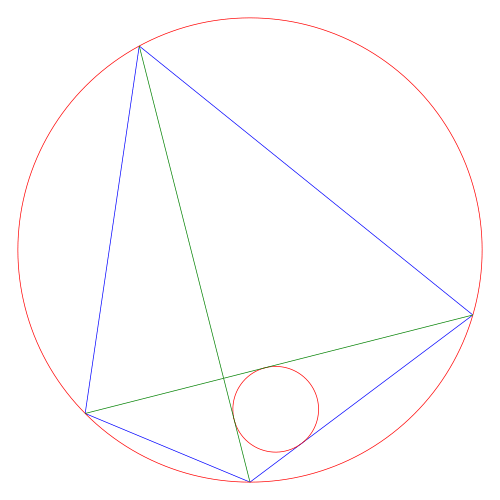
大円内に，天斜，地斜，左斜，右斜で構成される四辺形及びその対角線（乾斜，坤斜）を描く。天斜，乾斜，坤斜で囲まれる領域に小円を描く。
小円と大円の直径の（値の）積が 780 寸（本当は寸^2=歩？），また，天斜，左斜，右斜の長さがそれぞれ 39 寸，60 寸，25 寸のとき，地斜の長さはいかほどか。

四辺形の頂点を (x1, y1), (x2, y2), (x3, y3), (x4, y4)，小円の中心座標と半径を (x5, y5), r5 とおく。そのままでは未知数が 12 個，条件が 11 個で解けないが，図は回転しても一般性を失わないので，x1 = 0 になるように座標軸を定めれば方程式が解ける。また， x1 = 0 なら， y1 は大円の円周上になるので，未知数も方程式も 1 個ずつ減る。

using SymPy

function distance(x1, y1, x2, y2, x0, y0)
   p1, p2 = sympy.Point(x1, y1), sympy.Point(x2, y2)
   l = sympy.Line(p1, p2)
   l.distance(sympy.Point(x0, y0))^2  # 二乗距離を返す！！
end;

@syms x1, y1, x2, y2, x3, y3, x4, y4, x5, y5, r5, R;

x1 = 0
y1 = -R
eq1 = R * r5 - 780//4
eq2 = x2^2 + y2^2 - R^2
eq3 = x3^2 + y3^2 - R^2
eq4 = x4^2 + y4^2 - R^2
eq5 = (x4 - x1)^2 + (y4 - y1)^2 - 39^2
eq6 = (x4 - x3)^2 + (y4 - y3)^2 - 60^2
eq7 = (x1 - x2)^2 + (y1 - y2)^2 - 25^2
eq8 = distance(x4, y4, x1, y1, x5, y5) - r5^2 |> simplify
eq9 = distance(x4, y4, x2, y2, x5, y5) - r5^2 |> simplify
eq10 = distance(x3, y3, x1, y1, x5, y5) - r5^2 |> simplify;

# solve([eq1, eq2, eq3, eq4, eq5, eq6, eq7, eq8, eq9, eq10])

nlsolve() で解く。

println(eq1, ",")
println(eq2, ",")
println(eq3, ",")
println(eq4, ",")
println(eq5, ",")
println(eq6, ",")
println(eq7, ",")
println(eq8, ",")
println(eq9, ",")
println(eq10, ",")

   R*r5 - 195,
   -R^2 + x2^2 + y2^2,
   -R^2 + x3^2 + y3^2,
   -R^2 + x4^2 + y4^2,
   x4^2 + (R + y4)^2 - 1521,
   (-x3 + x4)^2 + (-y3 + y4)^2 - 3600,
   x2^2 + (-R - y2)^2 - 625,
   (-r5^2*(R^2 + 2*R*y4 + x4^2 + y4^2)^2 + x4^2*(R*x4 - R*x5 + x4*y5 - x5*y4)^2 + (x4*(R^2 + R*y4 + R*y5 + x4*x5 + y4*y5) - x5*(R^2 + 2*R*y4 + x4^2 + y4^2))^2)/(R^2 + 2*R*y4 + x4^2 + y4^2)^2,
   (-r5^2*(x2^2 - 2*x2*x4 + x4^2 + y2^2 - 2*y2*y4 + y4^2)^2 + (x2 - x4)^2*(x2*y4 - x2*y5 - x4*y2 + x4*y5 + x5*y2 - x5*y4)^2 + (y2 - y4)^2*(x2*y4 - x2*y5 - x4*y2 + x4*y5 + x5*y2 - x5*y4)^2)/(x2^2 - 2*x2*x4 + x4^2 + y2^2 - 2*y2*y4 + y4^2)^2,
   (-R^2*r5^2 + R^2*x3^2 - 2*R^2*x3*x5 + R^2*x5^2 - 2*R*r5^2*y3 + 2*R*x3^2*y5 - 2*R*x3*x5*y3 - 2*R*x3*x5*y5 + 2*R*x5^2*y3 - r5^2*x3^2 - r5^2*y3^2 + x3^2*y5^2 - 2*x3*x5*y3*y5 + x5^2*y3^2)/(R^2 + 2*R*y3 + x3^2 + y3^2),

using NLsolve

function nls(func, params...; ini = [0.0])
   if typeof(ini) <: Number
       r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=1e-14)
       v = r.zero[1]
   else
       r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=1e-14)
       v = r.zero
   end
   return v, r.f_converged
end;

function H(u)
   (x2, y2, x3, y3, x4, y4, x5, y5, r5, R) = u
   return [
R*r5 - 195,
-R^2 + x2^2 + y2^2,
-R^2 + x3^2 + y3^2,
-R^2 + x4^2 + y4^2,
x4^2 + (R + y4)^2 - 1521,
(-x3 + x4)^2 + (-y3 + y4)^2 - 3600,
x2^2 + (-R - y2)^2 - 625,
(-r5^2*(R^2 + 2*R*y4 + x4^2 + y4^2)^2 + x4^2*(R*x4 - R*x5 + x4*y5 - x5*y4)^2 + (x4*(R^2 + R*y4 + R*y5 + x4*x5 + y4*y5) - x5*(R^2 + 2*R*y4 + x4^2 + y4^2))^2)/(R^2 + 2*R*y4 + x4^2 + y4^2)^2,
(-r5^2*(x2^2 - 2*x2*x4 + x4^2 + y2^2 - 2*y2*y4 + y4^2)^2 + (x2 - x4)^2*(x2*y4 - x2*y5 - x4*y2 + x4*y5 + x5*y2 - x5*y4)^2 + (y2 - y4)^2*(x2*y4 - x2*y5 - x4*y2 + x4*y5 + x5*y2 - x5*y4)^2)/(x2^2 - 2*x2*x4 + x4^2 + y2^2 - 2*y2*y4 + y4^2)^2,
(-R^2*r5^2 + R^2*x3^2 - 2*R^2*x3*x5 + R^2*x5^2 - 2*R*r5^2*y3 + 2*R*x3^2*y5 - 2*R*x3*x5*y3 - 2*R*x3*x5*y5 + 2*R*x5^2*y3 - r5^2*x3^2 - r5^2*y3^2 + x3^2*y5^2 - 2*x3*x5*y3*y5 + x5^2*y3^2)/(R^2 + 2*R*y3 + x3^2 + y3^2),
   ]
end;

iniv = [big"-23.0", -22, -15, 28, 31, -9, 3, -22, 6, 32]
res = nls(H, ini=iniv)
println(res)
   (BigFloat[-23.07692307692307692307692307691865904585941003474930311365314461268297834238257, -22.88461538461538461538461538450049187950077181984566989711738965555646289279357, -15.50769230769230769230769230792675686699338875941266776383234390713069575421587, 28.5615384615384615384615384616459508480950144867108280676139955837025986961933, 31.19999999999999999999999999998122624448363949495361597070768953084622475373686, -9.099999999999999999999999999863248885904729542964274601211974716937721151767532, 3.599999999999999999999999999995741859144646799042250528533190648410558984504582, -22.29999999999999999999999999988215259415310464508394927693531668395582734424483, 6.000000000000000000000000000009441163418536999038475318876384580066842683370904, 32.49999999999999999999999999990015502464806610960030256664669973254443033639196], true)

x2 = -23.07692, y2 = -22.88462, x3 = -15.50769, y3 = 28.56154
x4 = 31.20000, y4 = -9.10000, x5 = 3.60000, y5 = -22.30000, r5 = 6.00000, R = 32.50000
となり，求める地斜の長さは三平方の定理より 52 と計算される。
地斜 = sqrt((x3 - x2)^2 + (y3 - y2)^2) = 52.00000

using Plots
using Printf

function circle(ox, oy, r, color=:red; beginangle=0, endangle=360)
  θ = beginangle:0.1:endangle
  x = r.*cosd.(θ)
  y = r.*sind.(θ)
  plot!(ox .+ x, oy .+ y, color=color, linewidth=0.5)
end;

function point(x, y, string="", color=:green, position=:left, vertical=:top; mark=true)
   mark && scatter!([x], [y], color=color, markerstrokewidth=0)
   annotate!(x, y, text(string, 10, position, color, vertical))
end;

function segment(x1, y1, x2, y2, color=:black; linestyle=:solid, linewidth=0.5)
   plot!([x1, x2], [y1, y2], color=color, linestyle=linestyle, linewidth=linewidth)
end;

function draw(more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (x2, y2, x3, y3, x4, y4, x5, y5, r5, R) = res[1]
   x1 = 0
   y1 = -R
   @printf("x1 = %.5f, y1 = %.5f, x2 = %.5f, y2 = %.5f, x3 = %.5f, y3 = %.5f\nx4 = %.5f, y4 = %.5f, x5 = %.5f, y5 = %.5f, r5 = %.5f, R = %.5f\n", x1, y1, x2, y2, x3, y3, x4, y4, x5, y5, r5, R)
   @printf("地斜 = sqrt((x3 - x2)^2 + (y3 - y2)^2) = %.5f\n", sqrt((x3 - x2)^2 + (y3 - y2)^2))
   plot([x1, x2, x3, x4, x1], [y1, y2, y3, y4, y1], color=:blue, lw=0.5)
   circle(0, 0, R)
   circle(x5, y5, r5)
   segment(x1, y1, x3, y3, :green)
   segment(x2, y2, x4, y4, :green)
   if more == true
       point(x1, y1, "(x1,y1)")
       point(x2, y2, "(x2,y2) ", :green, :right)
       point(x3, y3, "  (x3,y3)")
       point(x4, y4, " (x4,y4)")
       point(x5, y5, "(x5,y5;r5)", :green, :center)
       point(x5, y5, "小円", :red, :center, :bottom)
       point(R, 0, " R: 大円", :red)
       point((x3 + x4)/2, (y3 + y4)/2, "   左斜", :blue, mark=false)
       point((x2 + x3)/2, (y2 + y3)/2, " 地斜", :blue, mark=false)
       point((x1 + x2)/2, (y1 + y2)/2, "右斜", :blue, :right, mark=false)
       point((x1 + x4)/2, (y1 + y4)/2, "天斜", :blue, mark=false)
       point((x1 + x3)/2, (y1 + y3)/2, " 乾斜", :green, mark=false)
       point((x2 + x4)/2, (y2 + y4)/2, "    坤斜", :green, mark=false)
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
   else
      plot!(showaxis=false)
   end
end;

   x1 = 0.00000, y1 = -32.50000, x2 = -23.07692, y2 = -22.88462, x3 = -15.50769, y3 = 28.56154
   x4 = 31.20000, y4 = -9.10000, x5 = 3.60000, y5 = -22.30000, r5 = 6.00000, R = 32.50000
   地斜 = sqrt((x3 - x2)^2 + (y3 - y2)^2) = 52.00000