算額(その501)
山形県鶴岡市茨新田 鶴岡神明宮 文久2年(1862)
http://www.wasan.jp/yamagata/sinmei.html
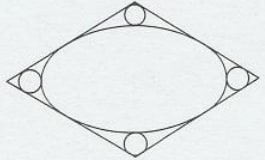
外円内に 4 本の斜線を引き,区画された領域に大円,中円,小円を入れる。
外円,大円,小円の直径がそれぞれ 125寸,99寸,21寸のとき,中円の直径はいかほどか。


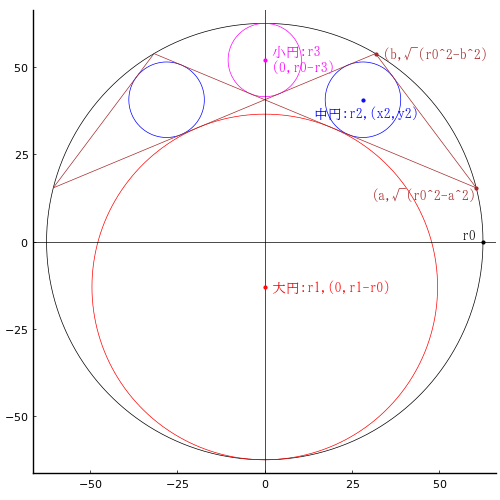
外円の半径と中心座標を r0, (0, 0 )
大円の半径と中心座標を r1, (0, r1 - r0)
中円の半径と中心座標を r2, (x2, y2)
小円の半径と中心座標を r3, (0, r0 - r3)
斜線と外円の交点座標を (a, sqrt(r0^2 - a^2), (b, sqrt(r0^2 - b^2)
とおき,以下の連立方程式の数値解を求める。
include("julia-source.txt");
using SymPy
@syms a, b, r0, r1, r2, x2, y2, r3
eq1 = distance(a, sqrt(r0^2 - a^2), -b, sqrt(r0^2 - b^2), 0, r1 - r0) - r1^2
eq2 = distance(a, sqrt(r0^2 - a^2), -b, sqrt(r0^2 - b^2), x2, y2) - r2^2
eq3 = distance(a, sqrt(r0^2 - a^2), -b, sqrt(r0^2 - b^2), 0, r0 -r3) - r3^2
eq4 = distance(-a, sqrt(r0^2 - a^2), b, sqrt(r0^2 - b^2), x2, y2) - r2^2
eq5 = distance(a, sqrt(r0^2 - a^2), b, sqrt(r0^2 - b^2), x2, y2) - r2^2;
using NLsolve
function nls(func, params...; ini = [0.0])
if typeof(ini) <: Number
r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=big"1e-40")
v = r.zero[1]
else
r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=big"1e-40")
v = r.zero
end
return v, r.f_converged
end;
function H(u)
(a, b, r2, x2, y2) = u
t1 = sqrt(-a^2 + r0^2)
t2 = sqrt(-b^2 + r0^2)
return [
-r1^2 + (t1 - t2)^2*(a^2*b - a*b^2 + a*r0^2 - a*r0*t1 + a*r0*t2 + a*r1*t1 - a*r1*t2 - a*t1*t2 - b*r0^2 - b*r0*t1 + b*r0*t2 + b*r1*t1 - b*r1*t2 + b*t1*t2)^2/(4*(a^2*t2 + a*b*t1 - a*b*t2 - b^2*t1 + 2*r0^2*t1 - 2*r0^2*t2)^2) + (-r0 + r1 - (-a^3*b - a^2*r0^2 + a^2*r0*t1 - 3*a^2*r0*t2 - a^2*r1*t1 + 3*a^2*r1*t2 + a^2*t1*t2 + a*b^3 + b^2*r0^2 + 3*b^2*r0*t1 - b^2*r0*t2 - 3*b^2*r1*t1 + b^2*r1*t2 - b^2*t1*t2 - 4*r0^3*t1 + 4*r0^3*t2 + 4*r0^2*r1*t1 - 4*r0^2*r1*t2)/(2*(a^2*t2 + a*b*t1 - a*b*t2 - b^2*t1 + 2*r0^2*t1 - 2*r0^2*t2)))^2, # eq1
-r2^2 + (x2 - (x2*(a^2*t2 + a*b*t1 - a*b*t2 - b^2*t1 + 2*r0^2*t1 - 2*r0^2*t2) + (t1 - t2)*(a^2*b + a^2*x2 - a*b^2 + a*r0^2 + a*y2*t1 - a*y2*t2 - a*t1*t2 + b^2*x2 - b*r0^2 + b*y2*t1 - b*y2*t2 + b*t1*t2 - 2*r0^2*x2 + 2*x2*t1*t2)/2)/(a^2*t2 + a*b*t1 - a*b*t2 - b^2*t1 + 2*r0^2*t1 - 2*r0^2*t2))^2 + (y2 - (y2*(a^2*t2 + a*b*t1 - a*b*t2 - b^2*t1 + 2*r0^2*t1 - 2*r0^2*t2) - (a + b)*(a^2*b + a^2*x2 - a*b^2 + a*r0^2 + a*y2*t1 - a*y2*t2 - a*t1*t2 + b^2*x2 - b*r0^2 + b*y2*t1 - b*y2*t2 + b*t1*t2 - 2*r0^2*x2 + 2*x2*t1*t2)/2)/(a^2*t2 + a*b*t1 - a*b*t2 - b^2*t1 + 2*r0^2*t1 - 2*r0^2*t2))^2, # eq2
-r3^2 + (t1 - t2)^2*(a^2*b - a*b^2 + a*r0^2 + a*r0*t1 - a*r0*t2 - a*r3*t1 + a*r3*t2 - a*t1*t2 - b*r0^2 + b*r0*t1 - b*r0*t2 - b*r3*t1 + b*r3*t2 + b*t1*t2)^2/(4*(a^2*t2 + a*b*t1 - a*b*t2 - b^2*t1 + 2*r0^2*t1 - 2*r0^2*t2)^2) + (r0 - r3 - (-a^3*b - a^2*r0^2 - a^2*r0*t1 + 3*a^2*r0*t2 + a^2*r3*t1 - 3*a^2*r3*t2 + a^2*t1*t2 + a*b^3 + b^2*r0^2 - 3*b^2*r0*t1 + b^2*r0*t2 + 3*b^2*r3*t1 - b^2*r3*t2 - b^2*t1*t2 + 4*r0^3*t1 - 4*r0^3*t2 - 4*r0^2*r3*t1 + 4*r0^2*r3*t2)/(2*(a^2*t2 + a*b*t1 - a*b*t2 - b^2*t1 + 2*r0^2*t1 - 2*r0^2*t2)))^2, # eq3
-r2^2 + (x2 - (x2*(a^2*t2 + a*b*t1 - a*b*t2 - b^2*t1 + 2*r0^2*t1 - 2*r0^2*t2) + (t1 - t2)*(-a^2*b + a^2*x2 + a*b^2 - a*r0^2 - a*y2*t1 + a*y2*t2 + a*t1*t2 + b^2*x2 + b*r0^2 - b*y2*t1 + b*y2*t2 - b*t1*t2 - 2*r0^2*x2 + 2*x2*t1*t2)/2)/(a^2*t2 + a*b*t1 - a*b*t2 - b^2*t1 + 2*r0^2*t1 - 2*r0^2*t2))^2 + (y2 - (y2*(a^2*t2 + a*b*t1 - a*b*t2 - b^2*t1 + 2*r0^2*t1 - 2*r0^2*t2) + (a + b)*(-a^2*b + a^2*x2 + a*b^2 - a*r0^2 - a*y2*t1 + a*y2*t2 + a*t1*t2 + b^2*x2 + b*r0^2 - b*y2*t1 + b*y2*t2 - b*t1*t2 - 2*r0^2*x2 + 2*x2*t1*t2)/2)/(a^2*t2 + a*b*t1 - a*b*t2 - b^2*t1 + 2*r0^2*t1 - 2*r0^2*t2))^2, # eq4
-r2^2 + (x2 - (a*(a*b - r0^2 + t1*t2) - (a - b)*(a*b + a*x2 - b*x2 - r0^2 + y2*t1 - y2*t2 + t1*t2)/2)/(a*b - r0^2 + t1*t2))^2 + (y2 - (2*t1*(a*b - r0^2 + t1*t2) - (t1 - t2)*(a*b + a*x2 - b*x2 - r0^2 + y2*t1 - y2*t2 + t1*t2))/(2*(a*b - r0^2 + t1*t2)))^2, # eq5
]
end;
(r0, r1, r3) = (125, 99, 21) .// 2
iniv = BigFloat[60.0, 33, 10, 29, 40]
res = nls(H, ini=iniv)
(BigFloat[60.5769230769230769230769230769230769230769230769230769230769230769230769357718, 31.73076923076923076923076923076923076923076923076923076923076923076923419539377, 10.81730769230769230769230769230769230769230769230769230769230769230769343490884, 28.12500000000000000000000000000000000000000000000000000000000000000000245224407, 40.62499999999999999999999999999999999999999999999999999999999999999999867465516], true)
r0 = 62.5; r1 = 49.5; r3 = 10.5
a = 60.5769; b = 31.7308; r2 = 10.8173; x2 = 28.125; y2 = 40.625
中円の直径 = 2r2 = 21.6346
中円の直径は 21.6346 ほどである。術では「二十一寸五十二分...」とあるので,一致しない。
実際の図は,算額に描かれたものとかなり異なる。
このようなことは算額においてはよくあることであるが,原因の一つは算額の図における各円の直径の割合が問に書かれたものと違うこと。
さらに,この算額の場合には外円の直径が「一百二十五寸」と書かれているのだが,「一」の部分が不鮮明であること。「二」でも「三」でもなさそうではあるのだが。
using Plots
function draw(more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(r0, r1, r3) = (125, 99, 21) .// 2
(a, b, r2, x2, y2) = res[1]
@printf("r0 = %g; r1 = %g; r3 = %g\n", r0, r1, r3)
@printf("a = %g; b = %g; r2 = %g; x2 = %g; y2 = %g\n", a, b, r2, x2, y2)
@printf("中円の直径 = 2r2 = %g\n", 2r2)
plot()
circle(0, 0, r0, :black)
circle(0, r1 - r0, r1, :red)
circle(x2, y2, r2, :blue)
circle(-x2, y2, r2, :blue)
circle(0, r0 - r3, r3, :magenta)
plot!([a, b, -a], [sqrt(r0^2 - a^2), sqrt(r0^2 - b^2), sqrt(r0^2 - a^2)], color=:brown, lw=0.5)
plot!([-a, -b, a], [sqrt(r0^2 - a^2), sqrt(r0^2 - b^2), sqrt(r0^2 - a^2)], color=:brown, lw=0.5)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:black, lw=0.5)
vline!([0], color=:black, lw=0.5)
point(0, r1 - r0, " 大円:r1,(0,r1-r0)", :red, :left, :vcenter)
point(x2, y2, " 中円:r2,(x2,y2)", :blue, :center, :top, delta=-delta)
point(0, r0 - r3, " 小円:r3\n (0,r0-r3)", :magenta, :left, :vcenter)
point(r0, 0, "r0 ", :black, :right, :bottom)
point(a, sqrt(r0^2 - a^2), "(a,√(r0^2-a^2)", :brown, :right)
point(b, sqrt(r0^2 - b^2), " (b,√(r0^2-b^2)", :brown, :left, :vcenter)
else
plot!(showaxis=false)
end
end;