算額(その505)
愛媛県大洲市新谷字山口 金刀比羅宮(現山口神社) 天明8年(1788)
http://www.wasan.jp/ehime/kotohira1.html
鈎股弦(直角三角形)内に,天地人の 3 個の等円が入っている。天円と地円の中心を結ぶ線分の長さが既知 a,鈎は股と弦の差より b だけ大きい。
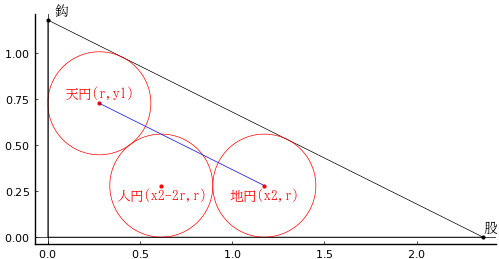
角が直角である頂点の座標を (0, 0)
鈎,股,弦の長さを鈎,股,弦
天円,地円,人円の半径と中心座標を r, (r, y1), (x2, r), (x2 - 2r, r)
として,以下の連立方程式の数値解を求める。
一般性を失わずに,a = 1 として解く。
include("julia-source.txt");
using SymPy
@syms 鈎, 股, 弦, r, y1, x2, x3, a, b
x2 = x3 + 2r
弦 = sqrt(鈎^2 + 股^2)
eq1 = (x2 - r)^2 + (y1 - r)^2 - a^2
eq2 = (鈎 - y1) + a + (股 - x2) - 弦
eq3 = (x3 - r)^2 + (y1 - r)^2 - 4r^2
eq4 = (y1 - r)/(x2 - r) - 鈎/股
eq5 = (弦 - 股 + b) - 鈎;
# res = solve([eq1, eq3, eq4, eq5, eq7], (鈎, 股, r, y1, x3))
using NLsolve
function nls(func, params...; ini = [0.0])
if typeof(ini) <: Number
r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=big"1e-40")
v = r.zero[1]
else
r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=big"1e-40")
v = r.zero
end
return v, r.f_converged
end;
function H(u)
(鈎, 股, r, y1, x3) = u
return [
-a^2 + (-r + y1)^2 + (r + x3)^2, # eq1
a - 2*r - x3 - y1 + 股 + 鈎 - sqrt(股^2 + 鈎^2), # eq2
-4*r^2 + (-r + x3)^2 + (-r + y1)^2, # eq3
(-r + y1)/(r + x3) - 鈎/股, # eq4
b - 股 - 鈎 + sqrt(股^2 + 鈎^2), # eq5
]
end;
a = 1
b = 0.9
iniv = iniv = BigFloat[1.4, 2.9, 0.33, 0.87, 0.77]
res = nls(H, ini=iniv)
(BigFloat[1.177379233363580301745329510921967893577066939399416499239250156741158075407193, 2.36009488557904520374835794798416053632581553124513131479814373696319717422653, 0.2793822120308020755416636618053848905748184134306487573156428076934921573204049, 0.7257863018027224197024724603072078876900065179854659272910142447388136755685596, 0.6154492741356734514186607085851531396329900169696428080777001398742020097906305], true)
a = 1, b = 0.9 のとき,等円の直径はほぼ 0.5587644240616042 である。
鈎 = 1.17738; 股 = 2.36009; 弦 = 2.63747; r = 0.279382; y1 = 0.725786; x2 = 1.17421; x3 = 0.615449
天円と地円の中心を結ぶ線分の長さ = sqrt((x2 - r)^2 + (y1 - r)^2)) = a = 1
鈎(1.17738) は 股(2.36009) と 弦(2.63747) の 差(0.277379) より b = 0.9 だけ大きい
等円の直径 = 0.558764 (0.5587644240616042)
using Plots
function draw(more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(鈎, 股, r, y1, x3) = res[1]
x2 = x3 + 2r
弦 = sqrt(鈎^2 + 股^2)
@printf("鈎 = %g; 股 = %g; 弦 = %g; r = %g; y1 = %g; x2 = %g; x3 = %g\n", 鈎, 股, 弦, r, y1, x2, x3)
@printf("天円と地円の中心を結ぶ線分の長さ = sqrt((x2 - r)^2 + (y1 - r)^2)) = a = %g\n", sqrt((x2 - r)^2 + (y1 - r)^2))
@printf("鈎(%g) は 股(%g) と 弦(%g) の 差(%g) より b = %g だけ大きい\n", 鈎, 股, 弦, 弦 - 股, 鈎 - (弦 - 股))
@printf("等円の直径 = %g (%.16g)\n", 2r, 2r)
plot([0, 股, 0, 0], [0, 0, 鈎, 0], color=:black, lw=0.5)
circle(r, y1, r)
circle(x2, r, r)
circle(x3, r, r)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:black, lw=0.5)
vline!([0], color=:black, lw=0.5)
point(0, 鈎, " 鈎", :black, :left, :bottom, delta=delta)
point(股, 0, "股", :black, :left, :bottom, delta=delta)
point(r, y1, "天円(r,y1)", :red, :center, :bottom, delta=delta)
point(x2, r, "地円(x2,r)", :red, :center, :top, delta=-delta)
point(x2 - 2r, r, "人円(x2-2r,r)", :red, :center, :top, delta=-delta)
segment(r, y1, x2, r, :blue)
else
plot!(showaxis=false)
end
end;




















