本格手打ちさぬきうどん 竜雲

高松市仏生山町 本格手打ちさぬきうどん 竜雲
もともとセルフうどんタイプのお店ではなかったが，いつからか知らないが，タブレットでオーダーするシステムになっていた。
セルフでないとちょっと気負ってメニューを選ぶ。美味しかったです。

算額（その1399）

算額（その1399）

十八 岩手県平泉町 弁慶堂（現在は地蔵堂にて保管） 安政6年(1859)
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市. http://www.wasan.jp/yamamura/yamamura.html
キーワード：円5個，外円，円弧2個
#Julia, #SymPy, #算額, #和算

外円の中に，外円と同じ直径の円弧（周長は外円の 1/3）で区切られた領域に 3 個の等円と 1 個の大円を容れる。外円の直径が与えられたとき，大円の直径を求める術を述べよ。

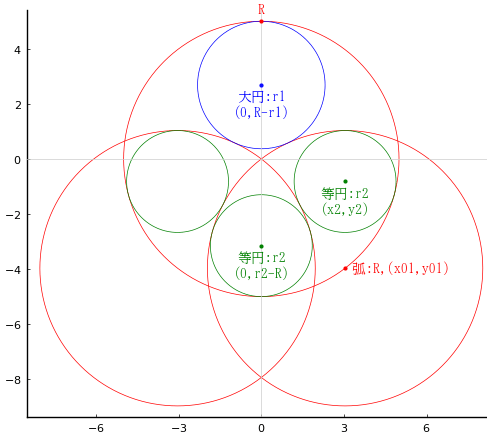
外円の半径と中心座標を R, (0, 0)
弧の半径と中心座標を R, (x01, -sqrt(R^2 - x01^2), (-x01, -sqrt(R^2 - x01^2)
大円の半径と中心座標を r1, (0, R - r1)
等円の半径と中心座標を r2, (0, r2 - R), (x2, y2)
とおき，以下の連立方程式を解く。
後にわかるが，x2 = x01 である。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy
@syms R::positive, r1::positive, r2::positive, x2::positive, y2::negative, x01::positive, y01::negative
eq1 = (x2 - x01)^2 + (y2 - y01)^2 - (R - r2)^2
eq2 = (x2 + x01)^2 + (y2 - y01)^2 - (R + r2)^2
eq3 = x2^2 + y2^2 - (R - r2)^2
eq4 = x01^2 + (R - r1 - y01)^2 - (R + r1)^2
eq5 = x01^2 + (r2 - R - y01)^2 - (R - r2)^2
eq6 = x01^2 + y01^2 - R^2
res = solve([eq1, eq2, eq3, eq4, eq5, eq6], (r1, r2, x2, y2, x01, y01))[1]

   (R*(-3*2^(1/3) + 6*2^(2/3) + 10)/34, R*(2 - 2^(1/3))/2, R*sqrt(4 - 2*2^(1/3))/2, 2^(1/3)*R*(1 - 2^(1/3))/2, R*sqrt(1 - 2^(1/3)/2), -2^(2/3)*R/2)

大円の半径は外円の半径の (-3*2^(1/3) + 6*2^(2/3) + 10)/34 = 0.463077740062488 倍である。
外円の直径が 10 寸のとき，大円の直径は 4.63077740062488 寸である。
ちなみに，小円の直径は 3.70039475052563 である。

# 大円の直径
res[1] |> println
res[1].evalf() |> println

   R*(-3*2^(1/3) + 6*2^(2/3) + 10)/34
   0.463077740062488*R

術は，3 / (∛16 + 1) + 1)*R/4 である。R の倍数を簡約化すると上で得られた式と同じになる。

# 術
@syms R, d
apart((3 / (cbrt(Sym(16)) + 1) + 1)/4, d) |> factor |> println

   (-3*2^(1/3) + 6*2^(2/3) + 10)/34

# 小円の直径
res[2] |> println
res[2].evalf() |> println

   R*(2 - 2^(1/3))/2
   0.370039475052563*R

全てのパラメータは以下のとおりである。

R = 10;  r1 = 4.63078;  r2 = 3.70039;  x2 = 6.08309;  y2 = -1.6374;  x01 = 6.08309;  y01 = -7.93701

x2 と x01 は全く同じ値である。
x2 = 6.0830870045772265, x01 = 6.0830870045772265

res[3] |> simplify |> println
res[5] |> simplify |> println

   R*sqrt(4 - 2*2^(1/3))/2
   R*sqrt(4 - 2*2^(1/3))/2

function draw(R, more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho") 
   (r1, r2, x2, y2, x01, y01) = (R*(-3*2^(1/3) + 6*2^(2/3) + 10)/34, R*(2 - 2^(1/3))/2, R*sqrt(4 - 2*2^(1/3))/2, 2^(1/3)*R*(1 - 2^(1/3))/2, R*sqrt(1 - 2^(1/3)/2), -2^(2/3)*R/2)
   @printf("外円の直径が %g のとき，大円の直径は %g，小円の直径は %g である。\n", 2R, 2r1, 2r2)
   @printf("R = %g;  r1 = %g;  r2 = %g;  x2 = %g;  y2 = %g;  x01 = %g;  y01 = %g\n", R, r1, r2, x2, y2, x01, y01)
   println("x2 = $x2, x01 = $x01")
   plot()
   circle(0, 0, R)
   circle2(x01, y01, R)
   circle(0, R - r1, r1, :blue)
   circle(0, r2 - R, r2, :green)
   circle2(x2, y2, r2, :green)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(x01, y01, " 弧:R,(x01,y01)", :red, :left, :vcenter)
       point(x2, y2, "等円:r2\n(x2,y2)", :green, :center, delta=-delta)
       point(0, r2 - R, "等円:r2\n(0,r2-R)", :green, :center, delta=-delta)
       point(0, R - r1, "大円:r1\n(0,R-r1)", :blue, :center, delta=-delta)
       point(0, R, "R", :red, :center, :bottom, delta=delta)
   end  
end;

draw(10/2, true)