算額(その1538)
(6) 大阪府茨木市大字総持寺 総持寺 嘉永7年(1854)
近畿数学史学会:近畿の算額「数学の絵馬を訪ねて」,平成4年5月16日 初版第一刷,大阪教育図書株式会社,大阪市.
キーワード:円6個,外円
#Julia, #SymPy, #算額, #和算
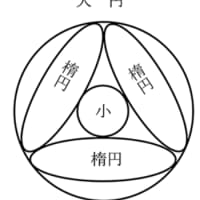
問は「如図大円之内五箇円径問」とだけあり,答は「中円一尺二寸,脇円八寸,小円六寸」とある。

注:大円の直径は中円の直径の 2 倍ではあるが,問で大円の直径を述べて置かなければ問が成り立たない。また,算額の図がどうなっているかのわからないが横に 3 個並んでいる円は等円のようだし,脇円,小円なのだろうが,答えにある直径を加えると2尺2寸になり,大円の直径より小さくなる。とりあえず脇円,小円を区別して立式するが,脇円が中円,小円,大円に接しているということは譲れない。また,「只云大円径二尺四寸」があるものとする。
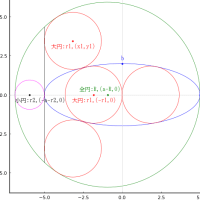
大円の半径と中心座標を R, (0, 0)
中円の半径と中心座標を r1, (0, r1)
脇円の半径と中心座標を r2, (R - r2, 0)
小円の半径と中心座標を r3, (0, 0)
とおき,以下の方程式を解く。
include("julia-source.txt")
# julia-source.txt ソース https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf
using SymPy
@syms R, r1, r2, r3
eq1 = r1 - R/2
eq2 = r3 - (2r1 - 2r2)
eq3 = r1^2 + (r3 + r3)^2 - (r1 + r2)^2
res = solve([eq1, eq2, eq3], (r1, r2, r3))[1] # 1 of 2
(R/2, R/3, R/3)
中円の半径は大円の半径の 1/2 倍,脇円は同じく 1/3 倍,小円も 1/3 倍ということで,脇円と小円は同じ大きさであるということになった。
大円の直径が 2 尺 4 寸のとき,中円の直径は 1 尺 2 寸,脇円,小円の直径は 8 寸である。
function draw(R, more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(r1, r2, r3) = R.*(1/2, 1/3, 1/3)
plot()
circle(0, 0, R)
circle22(0, r1, r1, :green)
circle2(R - r2, 0, r2, :blue)
circle(0, 0, r3, :magenta)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(0, R, "R", :red, :center, :bottom, delta=delta/2)
point(0, r1, "中円:r1,(0,r1)", :green, :center, delta=-delta/2)
point(R - r2, 0, "脇円:r2,(R-r2,0)", :blue, :center, delta=-delta/2)
point(0, 0, "小円:r3,(0,0)", :magenta, :center, delta=-delta/2)
end
end;
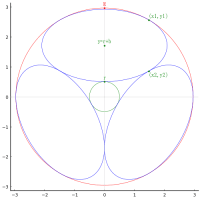
draw(24/2, true)