算額(その864)
岩手県平泉町 中尊寺阿弥陀堂(中尊寺地蔵院にて保管) 安政6年(1859)
http://www.wasan.jp/iwate/chusonji3.html
牧下英世:数学史を取り入れた授業実践―算額の教材化と総合的な学習―,2000筑波大学附属駒場論集第40集
https://tsukuba.repo.nii.ac.jp/record/6486/files/10.pdf
正方形内に正三角形と斜線,甲円と乙円が入っている。甲円と乙円の直径の差がわかっているとき,正方形の一辺の長さを求めよ。
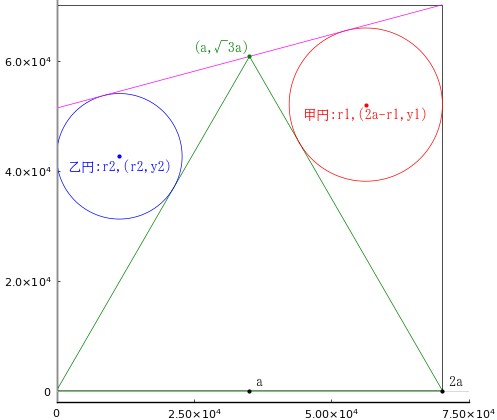
正方形の一辺の長さを 2a
甲円の半径と中心座標を r1, (2a - r1, y1)
乙円の半径と中心座標を r2, (r2, y2); r1 > r2
直径の差を K; r1 = r2 + K/2
とおき,以下の連立方程式を解く。
include("julia-source.txt");
using SymPy
@syms a::positive, r1::positive, y1::positive,
r2::positive, y2::positive, K::positive, d
s3 = √Sym(3)
r1 = r2 + K/2
eq1 = dist(2a, 0, a, s3*a, 2a - r1, y1) - r1^2
eq2 = dist(0, 0, a, s3*a, r2, y2) - r2^2
eq3 = dist(2a, 2a, a, s3*a, 2a - r1, y1) - r1^2
eq4 = dist(2a, 2a, a, s3*a, r2, y2) - r2^2
eq1 = numerator(apart(eq1, d)) |> simplify
eq2 = numerator(apart(eq2, d)) |> simplify
eq3 = numerator(apart(eq3, d)) |> simplify
eq4 = numerator(apart(eq4, d)) |> simplify;
# res = solve([eq1, eq2, eq3, eq4], (a, y1, r2, y2))
println(eq1, ", # eq1")
println(eq2, ", # eq2")
println(eq3, ", # eq3")
println(eq4, ", # eq4")
-K^2/16 - K*r2/4 - sqrt(3)*K*y1/4 - r2^2/4 - sqrt(3)*r2*y1/2 + y1^2/4, # eq1
-r2^2/4 - sqrt(3)*r2*y2/2 + y2^2/4, # eq2
-K^2/8 - sqrt(3)*K^2/16 - K*a/2 - K*r2/2 - sqrt(3)*K*r2/4 + K*y1/4 + sqrt(3)*a^2 + 2*a^2 - a*r2 - 2*a*y1 - sqrt(3)*a*y1 - r2^2/2 - sqrt(3)*r2^2/4 + r2*y1/2 + sqrt(3)*y1^2/4 + y1^2/2, # eq3
2*a^2 - a*r2 + sqrt(3)*a*r2 - sqrt(3)*a*y2 - a*y2 - r2^2/2 - sqrt(3)*r2^2/4 - r2*y2/2 + sqrt(3)*y2^2/4 + y2^2/2, # eq4
eq2, eq1 を解いて,r2, y1 を求める。
res1 = solve(eq2, r2)[1] # r2
res1 |> println
y2*(2 - sqrt(3))
res2 = solve(eq1, y1)[2] |> factor # y1 2番目が適解
res2 |> println
(sqrt(3) + 2)*(K + 2*r2)/2
eq3, eq4 に r2, y1 を代入して,変数消去する。
eq13 = eq3(y1 => res2, r2 => res1) |> simplify
eq13 |> println
sqrt(3)*K^2 + 7*K^2/4 - 4*K*a - 2*sqrt(3)*K*a + sqrt(3)*K*y2 + 2*K*y2 + sqrt(3)*a^2 + 2*a^2 - 4*a*y2 + y2^2
eq14 = eq4(y1 => res2, r2 => res1) |> simplify
eq14 |> println
2*a^2 - 6*a*y2 + 2*sqrt(3)*a*y2 - y2^2 + sqrt(3)*y2^2
eq14 から y2 を求めて,それを eq13 に代入して変数消去する。
res3 = solve(eq14, y2)[2] |> simplify # y2 2番目が適解
res3 |> println
a*(-sqrt(42 - 24*sqrt(3)) - sqrt(14 - 8*sqrt(3)) + 2*sqrt(3))/2
eq23 = eq13(y2 => res3) |> simplify
eq23 |> println
sqrt(3)*K^2 + 7*K^2/4 - K*a - 3*K*a*sqrt(42 - 24*sqrt(3))/2 - 5*K*a*sqrt(14 - 8*sqrt(3))/2 - 4*sqrt(3)*a^2 - a^2*sqrt(14 - 8*sqrt(3)) + a^2*sqrt(42 - 24*sqrt(3)) + 7*a^2
eq23 を a について求める。K だけを含む式になる。
res99 = solve(eq23, a)[1] |> simplify # a 1番目が適解
res99 |> println
K*(5*sqrt(14 - 8*sqrt(3)) + 3*sqrt(42 - 24*sqrt(3)) + 2 + 2*sqrt(sqrt(3) + 2))/(4*(-4*sqrt(3) - sqrt(2)*sqrt(7 - 4*sqrt(3)) + sqrt(6)*sqrt(7 - 4*sqrt(3)) + 7))
res99 には K が含まれているので simplify できないが,K にかかる係数は単に数値演算なので,簡約化できる。a = K*(4√3 + 7)/2 である。
@syms d
res999 = apart(res99/K, d)*K |> simplify # a
res999 |> println
K*(4*sqrt(3) + 7)/2
K に具体的な数値を代入すれば a の値が求まる。
res_a = res999(K => 5042).evalf() # a
res_a |> println
35113.0003435246
この後,逆順に代入していくことにより各変数の値を求めることができる。
res_y2 = res3(K => 5042, a => res_a).evalf() # y2
res_y2 |> println
42641.6741619770
res_r2 = res1(K => 5042, y2 => res_y2).evalf() # r2
res_r2 |> println
11425.8021556128
res_y1 = res2(K => 5042, r2 => res_r2).evalf() # y1
res_y1 |> println
52050.1742478581
甲円と乙円の直径の差が 5042 のとき,正方形の一辺の長さは 35113.0003435246 である。
その他のパラメータは以下のとおりである。
K = 5042; a = 35113; r1 = 13946.802; y1 = 52050.174; r2 = 11425.802; y2 = 42641.674
以下により,一挙に数値解を求めることもできる。
using NLsolve
function nls(func, params...; ini = [0.0])
if typeof(ini) <: Number
r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=big"1e-40")
v = r.zero[1]
else
r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=big"1e-40")
v = r.zero
end
return Float64.(v), r.f_converged
end;
function H(u)
(a, y1, r2, y2) = u
return [
-(K/2 + r2)^2 + (y1 - sqrt(3)*(sqrt(3)*a*y1 - a*(-K/2 - r2))/(4*a))^2 + (-K/2 - r2 - (-sqrt(3)*a*y1/2 + a*(-K/2 - r2)/2)/(2*a))^2, # eq1
-r2^2 + (r2 - (a*r2/2 + sqrt(3)*a*y2/2)/(2*a))^2 + (y2 - sqrt(3)*(a*r2 + sqrt(3)*a*y2)/(4*a))^2, # eq2
-(K/2 + r2)^2 + (-K/2 + a*(-a*(-K/2 - r2) + (-2*a + y1)*(-2*a + sqrt(3)*a))/(a^2 + (-2*a + sqrt(3)*a)^2) - r2)^2 + (-2*a + y1 - (-2*a + sqrt(3)*a)*(-a*(-K/2 - r2) + (-2*a + y1)*(-2*a + sqrt(3)*a))/(a^2 + (-2*a + sqrt(3)*a)^2))^2, # eq3
-r2^2 + (-2*a + y2 - (-2*a + sqrt(3)*a)*(-a*(-2*a + r2) + (-2*a + y2)*(-2*a + sqrt(3)*a))/(a^2 + (-2*a + sqrt(3)*a)^2))^2 + (-2*a + a*(-a*(-2*a + r2) + (-2*a + y2)*(-2*a + sqrt(3)*a))/(a^2 + (-2*a + sqrt(3)*a)^2) + r2)^2, # eq4
]
end;
K = 5042
iniv = BigFloat[35, 52, 11, 42].*1000
res = nls(H, ini=iniv)
([35113.000343524545, 52050.17424785807, 11425.802155612791, 42641.67416197693], true)
function draw(more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
s3 = √3
K = 5042
a = K*(4s3 + 7)/2
y2 = a*(2s3 - sqrt(42 - 24s3) - sqrt(14 - 8s3))/2
r2 = y2*(2 - s3)
y1 = (s3 + 2)*(K + 2*r2)/2
r1 = r2 + K/2
@printf("K = %.8g; a = %.8g; r1 = %.8g; y1 = %.8g; r2 = %.8g; y2 = %.8g\n", K, a, r1, y1, r2, y2)
plot([0, 2a, 2a, 0, 0], [0, 0, 2a, 2a, 0], color=:black, lw=0.5)
plot!([0, 2a, a, 0], [0, 0, √3a, 0], color=:green, lw=0.5)
circle(2a - r1, y1, r1)
circle(r2, y2, r2, :blue)
segment(0, 2a - 2(2a - √3a), 2a, 2a, :magenta)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(2a - r1, y1, "甲円:r1,(2a-r1,y1)", :red, :center, delta=-delta/2)
point(r2, y2, "乙円:r2,(r2,y2)", :blue, :center, delta=-delta/2)
point(a, √3a, "(a,√3a)", :green, :right, :bottom, delta=delta/2)
point(a, 0, " a", :black, :left, :bottom, delta=delta/2)
point(2a, 0, " 2a", :black, :left, :bottom, delta=delta/2)
plot!(xlims=(0, 75000))
end
end;



























