手打ちうどん 上田

高松市大田上町 手打ちうどん 上田
やや細麺，しっぽくうどん，牛肉を上に被せ，具材がでかい，甘くて旨い
現金払いのみ

算額（その1601）

算額（その1601）

宮城県角田市小田字斗蔵 斗蔵寺 明治42年(1909)
https://tajin.shiriagari.com/framepage5000.htm
    （リンク先の左のインデックスから選択）
キーワード：円5個，最大値
#Julia, #SymPy, #算額, #和算, #数学

交差する大円 2 個の隙間に，中円 1 個，小円 2 個を容れる。大円の直径が 10 寸のとき，小円の直径が最大になるのはどのようなときか，そしてそのときの小円の直径はいかほどか。

大円の半径と中心座標を r1, (r1 - r2, 0)
中円の半径と中心座標を r2, (0, 0)
小円の半径と中心座標を r3, (0, r2 + r3)
とおき，以下の連立方程式を解く。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy
@syms r1, r2, r3
eq = (r1 - r2)^2 + (r2 + r3)^2 - (r1 - r3)^2
res = solve(eq, r3)[1]
res |> println

    r2*(r1 - r2)/(r1 + r2)

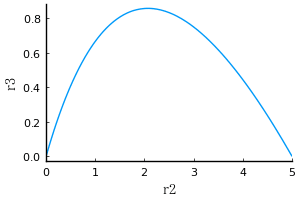
r3 は r2 の関数で，r1 が定数として固定されたとき，r3:r2 は下図のような関係にある。

たとえば，r1 が 10/2 のとき，r2 が 2 近辺で，r3 が最大になるようだ。

pyplot(size=(300, 200), grid=false, aspectratio=:none, label="", fontfamily="IPAMincho")
plot(res(r1 => 10/2), xlims=(0, 5), xlabel="r2", ylabel="r3")

最大値を取るときの r2 の値は，関数を微分し，0 になるときの値を求めればよい。

diff(res, r2) |> simplify |> println

    (-r2*(r1 - r2) + (r1 - 2*r2)*(r1 + r2))/(r1 + r2)^2

ans_r2 = solve(diff(res, r2), r2)[1]
ans_r2 |> println

    r1*(-1 + sqrt(2))

r1 = 10/2 のとき，r2 = 2.07106781186548 のとき，導関数は 0 になり，r3 は最大値を取る。

ans_r2(r1 => 10/2) |> println
ans_r2(r1 => 10/2).evalf() |> println

    -5.0 + 5.0*sqrt(2)
    2.07106781186548

r1 = 10/2，r2 = 2.07106781186548 のとき，r3 = 0.857864376269050 が最大値になる。

res(r2 => ans_r2)(r1 => 10/2) |> println
res(r2 => ans_r2)(r1 => 10/2).evalf() |> println

    0.5*sqrt(2)*(-1 + sqrt(2))*(10.0 - 5.0*sqrt(2))
    0.857864376269050

function draw(r1, more=false; r2 = 0)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
    r2 == 0 && (r2 = r1*(-1 + sqrt(2)))
    r3 = r2*(r1 - r2)/(r1 + r2)
    str = @sprintf("r1 = %g;; r2 = %.3g;  r3 = %.3g\n", r1, r2, r3)
    p = plot()
    circle2(r1 - r2, 0, r1)
    circle(0, 0, r2, :blue)
    circle22(0, r2 + r3, r3, :green)
    if more
        delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
        hline!([0], color=:gray80, lw=0.5)
        vline!([0], color=:gray80, lw=0.5)
        point(0, r1, str, :black, :center, :bottom, delta=delta/2, mark=false)
    end
    return p
end;

draw(10/2, true)

算額（その1600）

算額（その1600）

宮城県角田市小田字斗蔵 斗蔵寺 明治42年(1909)
https://tajin.shiriagari.com/framepage5000.htm
    （リンク先の左のインデックスから選択）
キーワード：二等辺三角形，正方形2個
#Julia, #SymPy, #算額, #和算, #数学

二等辺三角形内に大小の正方形を容れる。二等辺三角形の高さが 25 寸のとき，小正方形が最大になるときの二等辺三角形の底辺の長さと小正方形の一辺の長さはいかほどか。

二等辺三角形の高さを h，底辺の長さを 2a
大正方形の一辺の長さを 2b
小正方形の一辺の長さを 2c
とおき，以下の連立方程式を解く。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy
@syms a, b, c, h
eq1 = 2b/(a - b) - h/a
eq2 = 2c/(b - c) - h/a
eq3 = (h - 2b - 2c)/c - h/a
res = solve([eq1, eq2], (c, b));

# c
res[c] |> println

    a*h^2/(4*a^2 + 4*a*h + h^2)

h = 25 のとき，c は a の関数で下図のような関係にある。

pyplot(size=(300, 200), grid=false, aspectratio=:none, label="", fontfamily="IPAMincho")
plot(res[c](h => 25), xlims=(0, 30), xlabel="a", ylabel="c")

a が 10 近辺で，c が最大になるようだ。

最大値を取るときの a の値は，関数を微分し，0 になるときの値を求めればよい。

diff(res[c], a) |> simplify |> println

    h^2*(-2*a + h)/(8*a^3 + 12*a^2*h + 6*a*h^2 + h^3)

ans_a = solve(diff(res[c], a), a)[1]
ans_a |> println

    h/2

res[c](a => h/2)(h => 25) |> println
res[c](a => h/2)(h => 25).evalf() |> println

    25/8
    3.12500000000000

a = h/2 = 12.5 のとき，すなわち高さと底辺の長さが等しいときに小正方形の一辺の長さが最大 2*3.125 = 6.25 寸となる。

答では，小正方形の一辺の長さは 5 寸。
術では，高さを 5 で割る。
となっているが，それは上に示した最大値とは違う。小正方形の一辺の長さが 5 になるときの a を求めると 32.7254248593737，4.77457514062631 である。この間に c が最大になるときの a がある。

eq = a*h^2/(4*a^2 + 4*a*h + h^2) - c
ans_a = solve(eq, a)
ans_a |> println

    Sym{PyCall.PyObject}[(-h*(4*c - h) + sqrt(-h^3*(8*c - h)))/(8*c), (-4*c*h + h^2 - sqrt(h^3*(-8*c + h)))/(8*c)]

ans_a[1](h => 25, c => 5//2) |> println
ans_a[1](h => 25, c => 5//2).evalf() |> println

    25*sqrt(5)/4 + 75/4
    32.7254248593737

ans_a[2](h => 25, c => 5//2) |> println
ans_a[2](h => 25, c => 5//2).evalf() |> println

    75/4 - 25*sqrt(5)/4
    4.77457514062631

function draw(h, more=false; a = 0)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
    a == 0 && (a = h/2)
    b = a*h/(2a + h)
    c = a*h^2/(4*a^2 + 4*a*h + h^2)
    str = @sprintf("h = %g\na = %g\nb = %g\nc = %g", h, a, b, c)
    p = plot([a, 0, -a, a], [0, h, 0, 0], color=:green, lw=0.5)
    rect(-b, 0, b, 2b, :blue)
    rect(-c, 2b, c, 2b + 2c, :blue)
    delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
    point(-b/2, 1.8b, str, :red, :left, mark=false)
    if more
        delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
        hline!([0], color=:gray80, lw=0.5)
        vline!([0], color=:gray80, lw=0.5)
    end
    return p
end;

draw(25, true; a = 4.77457514062631)

算額（その1599）

算額（その1599）

宮城県角田市小田字斗蔵 斗蔵寺 明治42年(1909)
https://tajin.shiriagari.com/framepage5000.htm
    （リンク先の左のインデックスから選択）
キーワード：直角三角形，面積，最大値
#Julia, #SymPy, #算額, #和算, #数学

直角三角形の中に，図のように正方形を容れる。正方形の一辺の長さが 12 寸のとき，黒積が最大になるのはどのようなときか。またその最大値はいかほどか。

正方形の一辺の長さを a，黒積の直角三角形の頂点を (0, 0), (x, 0), (0, y)
鈎，股，弦をそのまま変数名とする。

証明はそんなに難しいものでもないが，直感でわかり，またそれが正しいことも簡単に示すことができる。

黒積が最大になるのは黒積が直角二等辺三角形のときである。斜辺が 12 寸のとき等辺は 12/√2 なので，黒積は (12/√2)^/2 = 36平方寸 である。

鈎 = 25.4558;  股 = 25.4558;  弦 = 36;  正方形の一辺の長さ = 12;  黒積 = 36

答えは 「4 歩」，術は「弦の冪（二乗）を 36 で割る」となっている。

図に描いてみると，元の直角三角形は黒積と相似（相似比は 3）なので，弦は 12*3 = 36 である。

確かに 36^2 / 36 = 36 となるが，「36」が「4 歩」というのはちょっとおかしい。一般的には「1 歩 = 36 平方尺 = 3600 平方寸」なので，単位に無頓着に「1 歩 = 36 平方寸」としてしまったのか?それにしても「4 歩 = 36」は理解しがたい。

以下は，無理やり SymPy で解く筋道である。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy
@syms 股, 鈎, 弦, 黒積, a, x, y
弦 = sqrt(鈎^2 + 股^2)
a = 12
eq1 = x^2 + y^2 - a^2
eq2 = y/x - 鈎/股
eq3 = 黒積 - x*y/2
res = solve([eq1, eq2, eq3], (黒積, x, y))[2]

    (72*股*鈎/(股^2 + 鈎^2), 12*股*sqrt(1/(股^2 + 鈎^2)), 12*鈎*sqrt(1/(股^2 + 鈎^2)))

黒積 = 72*股*鈎/(股^2 + 鈎^2)= 72*股*鈎/弦^2 である。

diff(res[1], 鈎) |> simplify |> println

    72*股*(股^2 - 鈎^2)/(股^2 + 鈎^2)^2

ans_鈎 = solve(diff(res[1], 鈎), 鈎)[2]  # 2 of 2
ans_鈎 |> println

    股

鈎 = 股 のとき（つまり，二等辺直角三角形のとき）に，黒積は最大になる。
黒積の直角三角形は外側の直角三角形と相似なので，黒積が最大のとき，x = y である。
x^2 + y^2 = 12 なので x = 6√2 である。
つまり，x = y = 6√2 の二等辺三角形のとき黒積が最大値 = (6√2)^2/2 = 36平方寸 である。

function draw(a, more=false)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
    x = y = 12/√2
    鈎 = 股 = 3x
    弦 = sqrt(鈎^2 + 股^2)
    黒積 = x*y/2
    @printf("鈎 = %g;  股 = %g;  弦 = %g;  正方形の一辺の長さ = %g;  黒積 = %g\n", 鈎, 股, 弦, a, 黒積)
    plot([0, 股, 0, 0], [0, 0, 鈎, 0], color=:green, lw=0.5)
    segment(x, 0, 0, y, :black)
    segment(0, y, y, y + x, :black)
    segment(x, 0, x + y, x, :black)
    plot!([0, x, 0, 0], [0, 0, y, 0], seriestype=:shape, color=:gray80, fillcolor=:gray80, lw=0.5)
    if more
        delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
        hline!([0], color=:gray80, lw=0.5)
        vline!([0], color=:gray80, lw=0.5)
        point(0, 鈎, " 鈎", :red, :left, :bottom, delta=delta/2)
        point(股, 0, "股", :red, :left, :bottom, delta=delta/2, deltax=0.7delta)
        point(0, y, " y", :red, :left, :vcenter)
        point(x, 0, "x", :red, :center, :bottom, delta=delta)
    end
end;

draw(12, true)