算額(その1598)
宮城県角田市小田字斗蔵 斗蔵寺 明治42年(1909)
https://tajin.shiriagari.com/framepage5000.htm
(リンク先の左のインデックスから選択)
キーワード:直角三角形,正方形,最大値
#Julia, #SymPy, #算額, #和算, #数学
直角三角形の中に中鉤を引き,中鉤と弦と股上に頂点を持つ正方形を容れる。股が 15 寸のとき,正方形の一辺が最長になるときその長さはいかほどか。

鈎,股をそのまま変数名とする。
中鈎上の正方形の頂点座標を (x, y)
弦上の中鈎の脚の座標を (x0, y0)
とおき,以下の連立方程式を解き,x, y, x0, y0 を求める。
それぞれは鈎,股の関数になる。
include("julia-source.txt");
# julia-source.txt ソース https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf
using SymPy
@syms 股, 鈎, x, y, x0, y0
eq1 = y/(股 - x - y) - 鈎/股
eq2 = x/y - 鈎/股
eq3 = (x0^2 + (鈎 - y0)^2)/(x0^2 + y0^2) - 鈎^2/股^2
eq4 = (x0- x)^2 + (y0 - y)^2 + (x + y - x0)^2 + (y0 - y)^2 - y^2
res = solve([eq1, eq2, eq3, eq4], (x, y, x0, y0))[1]
(股*鈎^2/(股^2 + 股*鈎 + 鈎^2), 股^2*鈎/(股^2 + 股*鈎 + 鈎^2), 股*鈎^2/(股^2 + 鈎^2), 股^2*鈎/(股^2 + 鈎^2))
正方形の一辺の長さ y は,股^2*鈎/(股^2 + 股*鈎 + 鈎^2) である。
# y
res[2] |> println
股^2*鈎/(股^2 + 股*鈎 + 鈎^2)
たとえば,股 = 15 のとき,鈎と正方形の一辺の長さの関係は下図のようになる。
pyplot(size=(300, 200), grid=false, aspectratio=:none, label="", fontfamily="IPAMincho")
plot(res[2](股 => 15), xlims=(0,100), xlabel="鈎", ylabel="正方形の一辺の長さ")
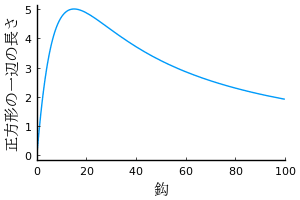
鈎が 10 〜 20 の間に正方形の一辺の長さが最大になるようである。
diff(res[2], 鈎) |> simplify |> println
股^2*(股^2 + 股*鈎 + 鈎^2 - 鈎*(股 + 2*鈎))/(股^2 + 股*鈎 + 鈎^2)^2
solve(diff(res[2], 鈎), 鈎)[2] |> println
股
鈎 = 股 のときに,正方形は最大になる。股が 15 寸のとき,正方形の一辺の長さは最長の 5 寸になる。
res[2](鈎 => 股, 股 => 15) |> println
225*股/(股^2 + 15*股 + 225)
function draw(股, more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
鈎 = 股
(x, y, x0, y0) = (股*鈎^2/(股^2 + 股*鈎 + 鈎^2), 股^2*鈎/(股^2 + 股*鈎 + 鈎^2), 股*鈎^2/(股^2 + 鈎^2), 股^2*鈎/(股^2 + 鈎^2))
plot([0, 股, 0, 0], [0, 0, 鈎, 0], color=:green, lw=0.5)
plot!([x, x + y, x + y, x, x], [0, 0, x, y], color=:blue, lw=0.5)
segment(0, 0, x0, y0, :black)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(0, 鈎, " 鈎", :red, :left, :bottom, delta=delta/2)
point(股, 0, "股", :red, :left, :bottom, delta=delta/2, deltax=0.7delta)
point(x0, y0, "(x0,y0)", :green, :left, :bottom, delta=delta/2)
point(x, y, "(x,y)", :blue, :right, :bottom, delta=delta/2)
point(x + y, y, "(x+y,y)", :blue, :left, :bottom, delta=delta/2)
end
end;
draw(15, true)



























