算額(その1218)
(17) 兵庫県姫路市飾磨区英賀宮町 英賀神社 明治12年(1879)
近畿数学史学会:近畿の算額「数学の絵馬を訪ねて」,平成4年5月16日 初版第一刷,大阪教育図書株式会社,大阪市.
キーワード:円1個,正方形5個
外円の中に合同な正方形を 5 個容れる。外円の直径が 10 寸のとき,正方形の一辺の長さはいかほどか。
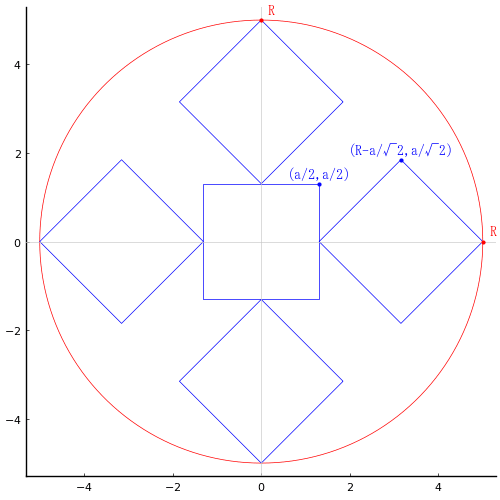
正方形の一辺の長さを a
外円の半径と中心座標を R, (0, 0)
とおき,以下の方程式を解く。
include("julia-source.txt");
using SymPy
@syms a::positive, R::positive
eq1 = √Sym(2)a + a/2 - R
res = solve(eq1, a)[1] |> simplify
res |> println
res(R => 10/2).evalf() |> println
2*R*(-1 + 2*sqrt(2))/7
2.61203874963741
正方形の一辺の長さ a は,外円の半径 R の 2(2√2 - 1)/7 倍である。
外円の直径が 10 寸のとき,正方形の一辺の長さは 5*2(2√2 - 1)/7 = 2.6120387496374144 寸である。
function draw_diamond(R, a, θ)
(y0, x0) = (R - a/√2).*sincos(pi*θ/180)
θ2 = 0:90:360
x = x0 .+ a/√2*cosd.(θ2)
y = y0 .+ a/√2*sind.(θ2)
plot!(x, y, color=:blue, lw=0.5)
end
function diamond(R, a)
for θ = 0:90:270
draw_diamond(R, a, θ)
end
end
function draw(R, more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
a = R*2(2√2 - 1)/7
@printf("外円の直径が %g のとき,正方形の一辺の長さは %g である。\n", 2R, a)
plot()
circle(0, 0, R)
rect(-a/2, -a/2, a/2, a/2, :blue)
diamond(R, a)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(0, R, " R", :red, :left, :bottom, delta=delta/2)
point(R, 0, " R", :red, :left, :bottom, delta=delta/2)
point(a/2, a/2, "(a/2,a/2)", :blue, :center, :bottom, delta=delta/2)
point(R - a/√2, a/√2, "(R-a/√2,a/√2)", :blue, :center, :bottom, delta=delta/2)
end
end;
draw(10/2, true)




























