〇×ゲームの手順は何通り？

〇×ゲームの手順は何通り？

締め切りが 2017/08/08 10:00 AM なので，その 1 分後に投稿されるように予約

設問

3×3のマス目を使って〇×ゲーム（三目並べ）を行います。
2人が交互に〇と×を空いているマスに記入していき、同じ記号が縦、横、斜めのいずれかに3つ並ぶとその記号の人が勝ちです。
すべてのマスが埋まっても3つ並ばないとき、その勝負は引き分けとなります。

例えば、以下の左図のような順に書いていったとき、×が横に3つ並んだので×の勝ちとなります。
一方、右図のような順に書いていったとき、いずれも3つ並ばないため、引き分けとなります。
（必ず〇の人から始め、勝負が決まった時点で終了するものとします）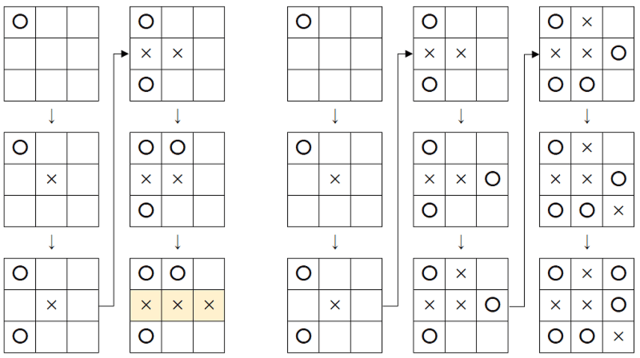

標準入力から整数 n が与えられたとき、ちょうど n 手でどちらか一方が勝つまでの手順が何通りあるかを求めてください。
なお、n は5以上9以下の整数です。

例えば、n = 5 のとき、〇の配置は、以下の8通りが考えられます。
それぞれについて、残りのマスのうち2箇所に×が入るため、手順を考えると全部で1440通りあります。

【入出力サンプル】
標準入力
5

標準出力
1440

================================================================

R では，惜しいところで計算時間オーバーになるので，Java で書き直すという，いつものパターン。
R では，permutations と combn を組み合わせて全ての場合をもうらする。
Java では，permutation の結果の unique  をとっていない（unique は計算時間がかかる）ので，n = 5, 6, 7 のときには重複してカウントすることになるので，その調整をする。

================================================================

R

permutations = function(n) {
    if (n == 1)
        return(matrix(1))
    else if (n < 2)
        stop("n must be a positive integer")
    z = matrix(1)
    for (i in 2:n) {
        x = cbind(z, i)
        a = c(1:i, 1:(i - 1))
        z = matrix(0, ncol = ncol(x), nrow = i * nrow(x))
        z[1:nrow(x), ] = x
        for (j in 2:i - 1) {
            z[j * nrow(x) + 1:nrow(x), ] = x[, a[1:i + j]]
        }
    }
    dimnames(z) = NULL
    z
}

f = function(n) {
    count = 0
    p = permutations(n)
    b = combn(9, n)
    for (i in 1:ncol(b)) {
        a = matrix((b[,i])[p], ncol=n)
        for (j in seq_len(nrow(a))) {
            x = a[j, ]
            board = integer(9)
            for (k in 1:9) {
                if (k%%2) {
                    board[x[k]] = 1
                } else {
                    board[x[k]] = 10
                }
                if (k >= 5) {
                    b1 = board[1] + board[2] + board[3]
                    b2 = board[4] + board[5] + board[6]
                    b3 = board[7] + board[8] + board[9]
                    b4 = board[1] + board[4] + board[7]
                    b5 = board[2] + board[5] + board[8]
                    b6 = board[3] + board[6] + board[9]
                    b7 = board[1] + board[5] + board[9]
                    b8 = board[3] + board[5] + board[7]
                    if (b1 == 3  || b2 == 3  || b3 == 3  || b4 == 3  ||
                        b5 == 3  || b6 == 3  || b7 == 3  || b8 == 3  ||
                        b1 == 30 || b2 == 30 || b3 == 30 || b4 == 30 ||
                        b5 == 30 || b6 == 30 || b7 == 30 || b8 == 30) {
                        count = count + (k == n)
                        break
                    }
                }
            }
        }
    }
    cat(count)
}

system.time(f(5)) # 1440, 0.268sec.
system.time(f(6)) # 5328，0.739sec.
system.time(f(7)) # 47952, 1.928sec.
system.time(f(8)) # 72576，3.516sec.
system.time(f(9)) # 81792, 3.812sec.

================================================================

Java

import java.util.Scanner;

public class Main {

    public static void main(String[] args) {
        long end;
        long start = System.currentTimeMillis();
        int i, j;
        int b1, b2, b3, b4, b5, b6, b7, b8;
        int n;
        int[][] z = permutations(9);
        int sizeZ = factorial(9);
        int count = 0;
        if (true) {
            Scanner cin = new Scanner(System.in);
            String line;
            line = cin.nextLine();
            n = Integer.parseInt(line);
        } else {
            n = 9;
        }
        for (i = 1; sizeZ >= i; i++) {
            int[] board = new int[10];
            for (j = 1; n >= j; j++) {
                if (j % 2 == 0) {
                    board[z[i][j]] = 1;
                } else {
                    board[z[i][j]] = 10;
                }
                if (j >= 5) {
                    b1 = board[1] + board[2] + board[3];
                    b2 = board[4] + board[5] + board[6];
                    b3 = board[7] + board[8] + board[9];
                    b4 = board[1] + board[4] + board[7];
                    b5 = board[2] + board[5] + board[8];
                    b6 = board[3] + board[6] + board[9];
                    b7 = board[1] + board[5] + board[9];
                    b8 = board[3] + board[5] + board[7];
                    if (b1 == 3  || b2 == 3  || b3 == 3  || b4 == 3  ||
                        b5 == 3  || b6 == 3  || b7 == 3  || b8 == 3  ||
                        b1 == 30 || b2 == 30 || b3 == 30 || b4 == 30 ||
                        b5 == 30 || b6 == 30 || b7 == 30 || b8 == 30) {
                        if (j == n) {
                            count++;
                        }
                        break;
                    }
                }
            }
        }
        System.out.println(count / factorial(9-n));
    }

    static int factorial(int n) {
        int i, result = 1;
        for (i = 1; n >= i; i++) {
            result *= i;
        }
        return result;
    }

    static int[][] permutations(int n) {
        int sizeZ = factorial(n);
        int sizeX = sizeZ / (n - 1);
        int[][] z = new int[sizeZ + 1][n + 1];
        int[][] x = new int[sizeX + 1][n + 1];
        int nrowZ, ncolZ, nrowX, ncolX;
        int i, i2, j, j2;
        z[1][1] = 1;
        nrowZ = ncolZ = 1;
        for (i = 2; n >= i; i++) {
            for (i2 = 1; nrowZ >= i2; i2++) {
                for (j2 = 1; ncolZ >= j2; j2++) {
                    x[i2][j2] = z[i2][j2];
                }
                x[i2][ncolZ + 1] = i;
            }
            nrowX = nrowZ;
            ncolX = ncolZ + 1;
            for (j = 1; i >= j; j++) {
                for (j2 = 1; nrowX >= j2; j2++) {
                    for (i2 = 1; ncolX >= i2; i2++) {
                        z[(j - 1) * nrowX + j2][i2] = x[j2][(j + i2 - 2) % i + 1];
                    }
                }
            }
            nrowZ = i * nrowX;
            ncolZ = ncolX;
        }
        return z;
    }

}