算額（その497）

算額（その497）

埼玉県さいたま市中央区円阿弥 日枝神社 慶応2年(1866) 正野友三郎一門奉納の算額

与野郷土資料館 展示Web解説（その21）
https://www.city.saitama.jp/004/005/004/005/yono/yonokyodo_tenjikaisetsu/p078011.html

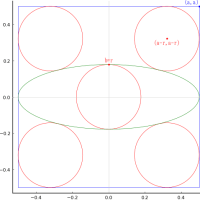
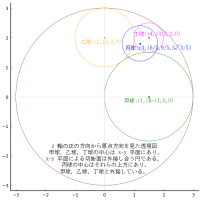
外円の中に2個の三角形と甲円が 2 個，乙円が 6 個入っている。乙円の直径が 1 寸のとき，甲円の直径はいかほどか。

外円の半径と中心座標を r0, (0, 0)
甲円の半径と中心座標を r1, (0, r2 + r1)
乙円の半径と中心座標を r2, (x2, y2), (r0 - r2, 0)
とおき，以下の連立方程式を解く。

ただし，一度に解くと solve() の能力的に解けないことと，数値解を求める場合にも収束が不安定になるので，まずは外円と甲円の r0, r1 を先に求める。

include("julia-source.txt");

using SymPy

@syms r0::positive, r1, r2, x2, y2;

x = sqrt(r0^2 - r2^2)
eq1 = r0*x - (r0 - 2r2)sqrt(x^2 + (r0 - r2)^2)
eq2 = (sqrt(r0^2 - r2^2) + sqrt(r0^2 - r2^2 + (r0 - r2)^2))r1 - sqrt(r0^2 - r2^2)*(r0 - r2);
res1 = solve([eq1, eq2], (r0, r1))

   2-element Vector{Tuple{Sym, Sym}}:
    (r2, r1)
    (8*r2, 3*r2)

解は 2 通り求まるが 2 番目のものが適解である。
すなわち，外円の半径は乙円の半径の 8 倍，甲円の半径は乙円の半径の 3 倍である。
乙円の直径が 1 寸のとき，外円の直径は 8 寸，甲円の直径は 3 寸である。

算額の問の答えとしては以上で十分であるが，図形を描くために右上にある乙円の中心座標を求める。

@syms r0, r1, r2, x2, y2;

(r0, r1) = (8r2, 3r2)
eq3 = y2*r0/(x2*sqrt(r0^2 - r2^2)) - 1
eq4 = x2^2 + y2^2 - (r0 - r2)^2
res2 = solve([eq3, eq4], (x2, y2))

   2-element Vector{Tuple{Sym, Sym}}:
    (-56*sqrt(127)*r2^2/(127*sqrt(r2^2)), -21*sqrt(889)*r2/127)
    (56*sqrt(127)*r2^2/(127*sqrt(r2^2)), 21*sqrt(889)*r2/127)

解は 2 通り求まるが 2 番目のものが適解である。

乙円の直径が 1 寸のとき，
甲円の直径 = 3;  外円の直径 = 8
r0 = 4;  r1 = 1.5;  r2 = 0.5;  x2 = 2.4846;  y2 = 2.46511 である。

using Plots

function draw(r2, more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r0, r1) = (8*r2, 3*r2)
   (x2, y2) = (56*sqrt(127)*r2^2/(127*sqrt(r2^2)), 21*sqrt(889)*r2/127)
   @printf("甲円の直径 = %g;  外円の直径 = %g;  r0 = %g;  r1 = %g;  r2 = %g;  x2 = %g;  y2 = %g\n",
       2r1, 2r0, r0, r1, r2, x2, y2)
   x = sqrt(r0^2 - r2^2)
   plot([x, 0, -x, x], [r2, r0, r2, r2], color=:red, lw=0.5)
   plot!([x, 0, -x, x], -[r2, r0, r2, r2], color=:red, lw=0.5)
   circle(0, 0, r0, :gray)
   circle(0, r2 + r1, r1, :blue)
   circle(0, -r2 - r1, r1, :blue)
   circle4(x2, y2, r2, :green)
   circle(r0 - r2, 0, r2, :green)
   circle(r2 - r0, 0, r2, :green)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
       point(0, r2 + r1, " 甲円:r1\n (0,r2+r1)", :blue, :left, :vcenter)
       point(x2, y2, "乙円:r2,(x2,y2)", :green, :center, :bottom, delta=delta/2)
       point(r0 - r2, 0, "r0-r2", :green, :center, :bottom, delta=delta/2)
       point(r0, 0, " r0", :black, :left, :bottom, delta=delta/2)
       point(r0, 0, " r0", :black, :left, :bottom, delta=delta/2)
       point(x, r2, "(√(r0^2-r2^2),r2)  ", :red, :right, :bottom, delta=delta/2)
       point(0, r2, " r2", :green, :left, :bottom, delta=delta/2)
   else
       plot!(showaxis=false)
   end
end;