Julia/SymPy: sin6°、cos6°、tan6°はどんな数？

sin6°、cos6°、tan6°はどんな数？
https://p-suugaku.blogspot.com/2021/11/sin6-cos6-tan6.html

tan(6°) はきれいな形にするのがちょっと面倒。

using SymPy

1. 6° = 36°-30° で加法定理，6° = 12° / 2 で半角の定理

1.1. sin(6°)

together(sind(Sym(6)))

1.2. cos(6°)

together(expand(cosd(Sym(6))))

together(cosd(Sym(6)))

1.3. tan(6°)

a1 = tand(Sym(6))

簡約化して，分子と分母

a2 = a1 |> simplify

a3 = a2 |> numer
-9 + sqrt(5) + sqrt(6*sqrt(5) + 30)

a4 = a2 |> denom
-sqrt(2)*sqrt(sqrt(5) + 5) - sqrt(3) + sqrt(15)

分母の有理化にかかる項

a5 = a4(-√Sym(2) => √Sym(2))
-sqrt(3) + sqrt(2)*sqrt(sqrt(5) + 5) + sqrt(15)

分母の有理化

a6 = a4 * a5 |> simplify # 8 - 8*sqrt(5)

更に有理化が必要。その項は

a7 = a6(-8√Sym(5)=>8√Sym(5)) # 8 + 8*sqrt(5)

二度の有理化の結果，分母は

a8 = simplify(a6 * a7) # -256

分子は

a9 = a3 * a5 * a7 |> simplify
-64*sqrt(10*sqrt(5) + 50) - 128*sqrt(3) + 64*sqrt(2*sqrt(5) + 10) + 128*sqrt(15)

分母の有理化の結果

a10 = a9/a8

@syms x

√(2√Sym(5)+10) を x,√(10√Sym(5)+50) を x√Sym(5) と置き，x で整理する

a11 = a10(√(2√Sym(5)+10)=>x,√(10√Sym(5)+50)=>x√Sym(5))

a12 = collect(a11, x)

a13 = 2√Sym(5) + 10 # 2*sqrt(5) + 10

a12 の x の係数

a14 = a12.coeff(x, 1) # -1/4 + sqrt(5)/4
a15 = √simplify(a13 * a14^2) # sqrt(5/2 - sqrt(5)/2)

定数項を足して全体

a16 = a15 + a12.coeff(x, 0)

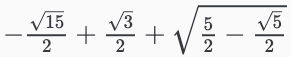
最終結果

a17 = a16 |> simplify

確認

a17 |> print
-sqrt(15)/2 + sqrt(3)/2 + sqrt(10 - 2*sqrt(5))/2

a17.evalf() # 0.105104235265676
a1.evalf()  # 0.105104235265676
tand(6)     # 0.10510423526567647

Julia/SymPy: 15°，18°，12°，72° の sin, cos, tan

sin15°、cos15°、tan15°はどんな数？ 
https://p-suugaku.blogspot.com/2021/10/sin15-cos15-tan15.html

sin18°、cos18°、tan18°はどんな数？ 
https://p-suugaku.blogspot.com/2021/10/sin18-cos18-tan18.html

sin72°、cos72°、tan72°はどんな数？
https://p-suugaku.blogspot.com/2021/10/sin72.html

sin12°、cos12°、tan12°はどんな数？
https://p-suugaku.blogspot.com/2021/10/sin12-cos12-tan12.html

結論：tan(12°) 以外は，簡単です。

using SymPy

1. 15° = 45° - 30° で加法定理

1.1. sin(15°)

together(sind(Sym(15))) |> print # (-sqrt(2) + sqrt(6))/4

1.2. cos(15°)

together(cosd(Sym(15))) |> print # (sqrt(2) + sqrt(6))/4

1.3. tan(15°)

tand(Sym(15)) |> print # 2 - sqrt(3)

2. 18° = 90° - 72° で加法定理

2.1. sin(18°)

together(sind(Sym(18))) |> print # (-1 + sqrt(5))/4

2.2. cos(18°)

together(cosd(Sym(18))) |> print # sqrt(2)*sqrt(sqrt(5) + 5)/4

2.3. tan(18°)

tand(Sym(18)) |> print # sqrt(5)*sqrt(5 - 2*sqrt(5))/5

3. 72° = 2π/5 で 5倍角の公式

3.1. sin(72°)

together(sind(Sym(72))) |> print # sqrt(2)*sqrt(sqrt(5) + 5)/4

3.2. cos(72°)

together(cosd(Sym(72))) |> print # (-1 + sqrt(5))/4

3.3. tan(72°)

tand(Sym(72)) |> print # sqrt(2*sqrt(5) + 5)

4. 12° = 30° - 18° で加法定理

4.1. sin(12°)

together(expand(sind(Sym(12)))) |>  print
(-sqrt(15) + sqrt(3) + sqrt(2)*sqrt(sqrt(5) + 5))/8

4.2. cos(12°)

together(expand(cosd(Sym(12)))) |> print
(-1 + sqrt(5) + sqrt(6)*sqrt(sqrt(5) + 5))/8

4.3. tan(12°)

a1 = together(expand(tand(Sym(12))))

分子と分母

a2 = numer(a1)
a3 = denom(a1)

分母の有理化のために分子・分母に掛ける項

a4 = a3(√Sym(15)=>-√Sym(15))

分子と分母

a5 = a2*a4
a6 = simplify(a3*a4) # 30√5 + 150

もう一度分母の有理化のために分子・分母に掛ける項

a7 = a6(150=>-150)   # 30√5 - 150

分子と分母

a8 = a5*a7 |> simplify
a9 = a6*a7 |> simplify # 18000

分母を有理化した結果

a10 = a8 / a9

@syms x

√(5-2√5) を x，√(25-10√5) を x√5 とおく

a11 = a10(√(5 - 2√Sym(5)) => x, √(25-10√Sym(5)) => x√Sym(5))

x で整理する

a12 = a11.collect(x)

a13 = 5 - 2√Sym(5)    # 5 - 2√5
a14 = a12.coeff(x, 1) # 1/2 - sqrt(5)/2
a15 = a13 * a14^2
a16 = simplify(a15)   # 25/2 - 11*sqrt(5)/2

a14 < 0 ゆえ，a17 も負になるので，平方根の符号は -

a17 = simplify(-sqrt(a16))

最終結果

a18 = together(a17 + a12.coeff(x, 0))

確認

a18 |> print
(-sqrt(15) - sqrt(2)*sqrt(25 - 11*sqrt(5)) + 3*sqrt(3))/2

a18.evalf() # 0.212556561670022
a1.evalf()  # 0.212556561670022
tand(12)    # 0.21255656167002213

Julia/SymPy: sin3°、cos3°、tan3°はどんな数？

sin3°、cos3°、tan3°はどんな数？ 
https://p-suugaku.blogspot.com/2021/12/sin3-cos3-tan3.html

「答え一発！！」とはなかなかいかない。

今回の問題では，平方根内の因数を平方根外にくくりだすこととその逆，分母の有理化の操作が必要だった。

残念ながら，今の時点では SymPy はそのどちらも自動的にやってくれないので，小細工を弄さねばならない。

でもまあ，式の変換時の間違いに心配しなくても良いので，慣れてしまえば便利な道具ではある。

1. sin(3°)

using SymPy
@syms a

a1 = sind(Sym(3))

a2 = simplify(together(a1))

Sym5 = Sym(5) # 5

ちょっと見通しを良くするために √(5 - √5) => a とする

a3 = a2(√(5-√Sym5)=>a)



まとめる

a4 = collect(a3, a)



a4 で a の1次の項を取り出す。

a5 = a4.coeff(a, 1)



a6 = √(5-√Sym5) * a5



a6 の二乗

a7 = a6^2



a7 の平方根。ただし，a6 < 0 ゆえ，符号は -

a8 = -sqrt(expand(a7*8^2))/8



a4 で a の 0 次の項を取り出す

a9 = a4.coeff(a, 0)



最終結果：a4 の式全体

a10 = a8 + a9

確認

a10 |> print
-sqrt(-10*sqrt(3) - 2*sqrt(15) + 4*sqrt(5) + 20)/8 - sqrt(6)/16 - sqrt(2)/16 + sqrt(10)/16 + sqrt(30)/16

a10.evalf() # 0.0523359562429438
a1.evalf()  # 0.0523359562429438
sind(3)     # 0.052335956242943835

2. cos(3°)

b1 = cosd(Sym(3))



Sym5 = Sym(5) # 5

ちょっと見通しを良くするために √(5 - √5) => a とする

b4 = collect(simplify(together(b1))(√(5-√Sym5)=>a), a)

b4 で a の1次の項を取り出す

b5 = b4.coeff(a, 1)



b6 = √(5-√Sym5) * b5



b6 の二乗

b7 = b6^2



b7 の平方根。ただし，b6 > 0 ゆえ，符号は +

b8 = sqrt(expand(b7*8^2))/8

b4 で a の 0 次の項を取り出す

b9 = b4.coeff(a, 0)



b4 の式全体

b10 = b8 + together(b9)

確認

b10 |> print
(-sqrt(10) - sqrt(6) + sqrt(2) + sqrt(30))/16 + sqrt(2*sqrt(15) + 4*sqrt(5) + 10*sqrt(3) + 20)/8

b10.evalf() # 0.998629534754574
b1.evalf()  # 0.998629534754574
cosd(3)     # 0.9986295347545738

3. tan(3°)

c1 = tand(Sym(3))



c2 = simplify(c1)

c2 を有理化する

まず，c2 の分子，分母を取り出す

numerator = numer(c2)



denominator1 = denom(c2)



有理化する

denominator2 = denominator1(√Sym(6)=>-√Sym(6))

有理化する

分子

a = simplify(numerator * denominator2)



分母

b = simplify(denominator1 * denominator2)



もう一度有理化する

b2 = b(8=>-8)

a = simplify(a * b2)



b = simplify(b * b2) # 256

有理化のあと，展開する

c3 = expand(a)/b



@syms x

√(30-6√5) を x√6, √(10-2√5) を x*√2 に置き換える

c4 = c3(√(30-6√Sym(5))=>x√Sym(6), √(10-2√Sym(5))=>x*√Sym(2))



x^2 を 5-√5 に置き換える

c5 = c4(x^2=>5-√Sym(5))



c6 = simplify(c5)


x の次数でまとめる

c7 = collect(c6, x)



1 次の項を取り出す

c8 = c7.coeff(x, 1)



0 次の項を取り出す

c9 = c7.coeff(x, 0)

c8^2 を √ の中に入れる

c10 = (5 - √Sym(5)) * c8^2



c11 = simplify(c10)



c12 = simplify(sqrt(c11))



c7 の式全体。単に c12 + c9 でよい

c13 = c12+together(c9)



確認

c13 |> print
(-3*sqrt(3) - sqrt(15) + 4 + 2*sqrt(5))/2 + sqrt(-28*sqrt(15) - 60*sqrt(3) + 46*sqrt(5) + 110)/2

c13.evalf() # 0.0524077792830412
c1.evalf()  # 0.0524077792830412
tand(3)     # 0.05240777928304121

なお，元のページの最終の式中 96√5 は上述の通り，46√5 の間違い