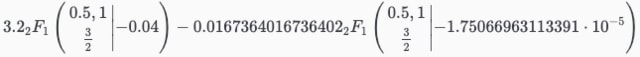Julia/SymPy: 無限級数の極限--2

using SymPy
@syms n

summation(1/2^n, (n, 0, oo)) # 2

summation(1/2^n, (n, 1, oo)) # 1

summation(1/((2n+1)*(2n+3)), (n, 1, oo)) # 1/6

summation(1/(n*(n+2)), (n, 1, oo)) # 3/4

summation(1/3^(n-1) - 1/4^n, (n, 1, oo)) # 7/6

summation(1/3^n, (n, 0, oo)) # 3/2

summation(n/(2n+1), (n, 1, oo)) # ∞

summation(1/(n*(n+2)*(n+3)), (n, 1, oo)) # 5/36

summation(cos(n*π/2)/2^n, (n, 1, oo)) |> print  # Sum(cos(pi*n/2)/2^n, (n, 1, oo))
summation(cos(n*π/2)/2^n, (n, 1, 1000)).evalf() # -1/5

summation(π/12 *(1/9)^(n-1), (n, 1, oo)) # 0.294524311274043
3/32*π # 0.2945243112740431

summation(1/(n*(n+1)), (n, 1, oo)) # 1

summation(9*10^(-n), (n, 1, oo)) # 1

summation(1/factorial(n), (n, 0, oo)) # ℯ ネイピアの定数

summation(1/(2n+1)^2, (n, 0, oo)) # π²/8

summation(1/n^2, (n, 1, oo)) # π²/6

summation(1/n^4, (n, 1, oo)) # π⁴/90

summation(1/n^6, (n, 1, oo)) # π⁶/945

summation(1/n^8, (n, 1, oo)) # π⁸/9450

summation(1/n^3, (n, 1, oo)) # ζ(3) = 1.20205690315959

summation(1/n^5, (n, 1, oo)) # ζ(5) = 1.03692775514337

summation(1/n^7, (n, 1, oo)) # ζ(7) = 1.00834927738192

summation(1/n^9, (n, 1, oo)) # ζ(9) = 1.00200839282608

Julia/SymPy: 無限級数の極限

using SymPy

@syms n

1. log(2)

e1 = summation((-1)^(n-1)/n, (n, 1, oo));

e1 |> print # log(2)

e1.evalf()  # 0.693147180559945

2. フーリエ級数

e2 = summation(1/n^2, (n, 1, oo));

e2 |> print # pi^2/6

√(e2 * 6).evalf() # 3.14159265358979

3. グレゴリー・ライプニッツ級数

e3 = summation((-1)^(n-1) / (2n - 1), (n, 1, oo));

e3 |> print  # pi/4

4*e3.evalf() # 3.14159265358979

4. マチンの公式

e4 = summation(16*(-1)^n/(2n+1)*(1/5)^(2n+1) - 4*(-1)^n/(2n+1)*(1/239)^(2n+1), (n, 0, oo))

e4 |> print # 3.2*hyper((0.5, 1), (3/2,), -0.04) - 0.0167364016736402*hyper((0.5, 1), (3/2,), -1.75066963113391e-5)

e4.evalf() # 3.14159265358979

hyper((a, b), (c,), z) は Gauss hypergeometric function の ₂F₁(a, b, c, z)

using HypergeometricFunctions

3.2 * _₂F₁(0.5, 1, 3/2, -0.04) - 0.0167364016736402 * _₂F₁(0.5, 1, 3/2, -1.75066963113391e-5) # 3.1415926535897936

Python の sympy では以下で評価できるが，Julia では（いまのところ）できない。

>>> (3.2*hyper((0.5, 1), (3/2,), -0.04) - 0.0167364016736402*hyper((0.5, 1), (3/2,), -1.75066963113391e-5)).evalf() # 3.14159265358979

5. ラマヌジャン式

e5 = (-1)^n*factorial(4n)*(1123 + 21460n) / 882^(2n+1) / (4^n * factorial(n))^4

4/summation(e5, (n, 0, 0)).evalf() # 3.14158504007124
4/summation(e5, (n, 0, 1)).evalf() # 3.14159265359762
4/summation(e5, (n, 0, 2)).evalf() # 3.14159265358979

収束の速さは目を瞠るものがある。

res = 0
for n = 0:12
    res += (-1)^n * factorial(big(4)n) * (1123 + 21460n) / big(882)^(2n+1) / (4^n * factorial(big(n)))^4
    println("$n $(4/res)")
end
println("pi:", big(pi))

0 3.14158504007123775601068566340160284951024042742653606411398040961709706144257
1 3.141592653597622014268275179202291563387123765940278924800131654234958957780921
2 3.141592653589793229887677088812011582500396626398585829522573327158139832285541
3 3.141592653589793238462653137021443968203070363083330244371464119910981874588252
4 3.141592653589793238462643383268142159665117427792501809002405604153156497729344
5 3.141592653589793238462643383279502897644492229727493144410492231930577371459383
6 3.141592653589793238462643383279502884197153296192775704368162768434095479750287
7 3.141592653589793238462643383279502884197169399394559174859992564888677720166504
8 3.141592653589793238462643383279502884197169399375105797313049395317182201783169
9 3.141592653589793238462643383279502884197169399375105820974973531650835366122329
10 3.141592653589793238462643383279502884197169399375105820974944592272262921459799
11 3.14159265358979323846264338327950288419716939937510582097494459230781645012978
12 3.141592653589793238462643383279502884197169399375105820974944592307816406286094
pi:3.141592653589793238462643383279502884197169399375105820974944592307816406286198

Julia/SymPy: 立方根の方程式

立方根の方程式
https://p-suugaku.blogspot.com/2021/09/rippoukon-houteishiki.html

a = 1/3 のとき，以下の方程式 f(x) = 0 を解けという問題。要するに立方根を含む問題である。
f(x) = (3x+2)^a - (x-2)^a - (x+2)^a

素直に SymPy で解いてみると

using SymPy
@syms a, x

solve((3x+2)^(1/3) - (x-2)^(1/3) - (x+2)^(1/3)) |> float

で，-2.0，2.074772708486752 という 2 つの解が示される（後で示すが，3 つあるはず）。

件の解答例は (2 ± √19) / 3 になっているが，明らかにおかしい。
(2+√19)/3 #  2.119632981180225
(2-√19)/3 # -0.7862996478468913
f((2+√19)/3)(a=>1/3) # −0.0663385359996638
f((2-√19)/3)(a=>1/3) # -1.41493963273732 - 0.60319058562597i
どのようにおかしいか，図にしてみようと plot() で描こうとしたが，x の値によって，上で示した Base で定義した関数 f(x) が計算できない（虚数になる）ので，とりあえず中断。

回答例のどこがおかしいのかな?と追試してみると

>   問の方程式の両辺を 3 乗したものは

　　　　

>   となります。これを整理して

　　　　

としているが，1 行目の右辺が 3 乗されていないのがそもそもの間違い。

正しく計算すれば，5*x^3 + 3*x^2 - 21*x - 14 = 0 となる。

a1 = 5x^3 + 3x^2 - 21x - 14
a2 = solve(a1)
# Sym[-2, 7/10 - 3*sqrt(21)/10, 7/10 + 3*sqrt(21)/10]

a2[2].evalf() # −0.674772708486752
a2[3].evalf() #  2.07477270848675
a1(x=>a2[1]) # 0
a1(x=>a2[2]).evalf() # 3.0 * 10^(-123)
a1(x=>a2[3]).evalf() # -1.0 * 10^(-122)

図に描いてみよう。

plot(a1, xlims=(-2.1, 2.2), labels="")
hline!([0], labels="")
vline!(a2, labels="")

しかし，そもそもは立方根を含む元の式，以下の a3 に代入して 0 になるか確認しなければならない。

a3 = ((3x+2)^a - (x-2)^a - (x+2)^a)(a => 1/3)
a3(x=>a2[1]).evalf() |>print # 0
a3(x=>a2[2]).evalf() |>print # -1.64761112632243 - 0.951248727302079*I
a3(x=>a2[3]).evalf() |>print # -5.73973140632228e-17

つまり，x = −0.674772708486752 の場合には虚数になるので，不適解ということで，
x = -2, 2.07477270848675 の 2 つが解であるということ。
https://www.wolframalpha.com によってもこの 2 つの解が示される。

Julia/SymPy: sin(42°)，cos(42°)，tan(42°)

Julia/SymPy: sin(42°)，cos(42°)，tan(42°)

Julia/SymPy: sin(39°)，cos(39°)，tan(39°)

Julia/SymPy: sin(39°)，cos(39°)，tan(39°)

Julia/SymPy: sin(36°)，cos(36°)，tan(36°)

Julia/SymPy: sin(36°)，cos(36°)，tan(36°)

Julia/SymPy: sin(33°)，cos(33°)，tan(33°)

Julia/SymPy: sin(33°)，cos(33°)，tan(33°)

Julia/SymPy: sin(27°)，cos(27°)，tan(27°)

Julia/SymPy: sin(27°)，cos(27°)，tan(27°)

Julia/SymPy: sin(24°)，cos(24°)，tan(24°)

Julia/SymPy: sin(24°)，cos(24°)，tan(24°)

Julia/SymPy: sin(21°)，cos(21°)，tan(21°)

Julia/SymPy: sin(21°)，cos(21°)，tan(21°)

Julia/SymPy: x・logx の積分

x・logx の積分

Julia/Sym Py: asin(), acos(), atan() の積分

SymPy 一発

sin^-1(x)，cos^-1(x)，tan^-1(x) は asin(x), acos(x), atan(x) のこと。