算額(その394)
東京都府中市 大國魂神社 明治18年(1885)
佐藤健一『多摩の算額』
山口正義『やまぶき』第8号
https://yamabukiwasan.sakura.ne.jp/ymbk8.pdf
もとは以下のものか。
東都愛宕山 天明8年戊申5月(1788)
東都大久保住 小林勝之助佐政
藤田貞資(1789):神壁算法
http://www.wasan.jp/jinpeki/jinpekisanpo1.pdf
直線の上に,大円,小円,甲円,乙円,丙円が載っている。甲円,乙円の直径がそれぞれ 45 寸,40 寸のとき,丙円の直径を求めよ。
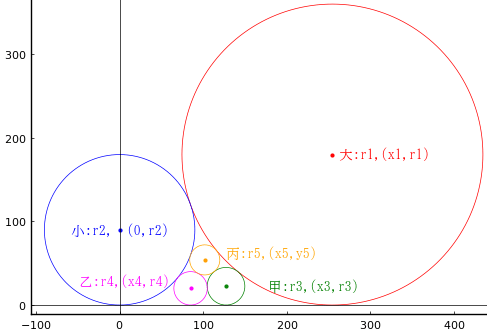
大円の半径と中心座標を r1, (x1, r1)
小円の半径と中心座標を r2, (0, r2)
甲円の半径と中心座標を r3, (x3, r3)
乙円の半径と中心座標を r4, (x4, r4)
丙円の半径と中心座標を r5, (x5, y5)
として,以下の連立方程式を立て,nlsove() で数値解を求める。
include("julia-source.txt");
using SymPy
@syms r1::positive, x1::positive, r2::positive, r3::positive,
x3::positive, r4::positive, x4::positive, r5::positive,
x5::positive, y5::positive;
(r3, r4) = (45, 40) .// 2
eq1 = x1^2 + (r1 - r2)^2 - (r1 + r2)^2
eq2 = (x1 - x3)^2 + (r1 - r3)^2 - (r1 + r3)^2
eq3 = (x1 - x5)^2 + (r1 - y5)^2 - (r1 + r5)^2
eq4 = x4^2 + (r2 - r4)^2 - (r2 + r4)^2
eq5 = x5^2 + (r2 - y5)^2 - (r2 + r5)^2
eq6 = (x3 - x4)^2 + (r3 - r4)^2 - (r3 + r4)^2
eq7 = (x3 - x5)^2 + (y5 - r3)^2 - (r3 + r5)^2
eq8 = (x5 - x4)^2 + (y5 - r4)^2 - (r4 + r5)^2;
# res = solve([eq1, eq2, eq3, eq4, eq5, eq6, eq7, eq8], (r1, x1, r2, x3, x4, r5, x5, y5))
using NLsolve
function nls(func, params...; ini = [0.0])
if typeof(ini) <: Number
r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=1e-14)
v = r.zero[1]
else
r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=1e-14)
v = r.zero
end
return v, r.f_converged
end;
function H(u)
(r1, x1, r2, x3, x4, r5, x5, y5) = u
return [
x1^2 + (r1 - r2)^2 - (r1 + r2)^2, # eq1
(r1 - 45/2)^2 - (r1 + 45/2)^2 + (x1 - x3)^2, # eq2
-(r1 + r5)^2 + (r1 - y5)^2 + (x1 - x5)^2, # eq3
x4^2 + (r2 - 20)^2 - (r2 + 20)^2, # eq4
x5^2 - (r2 + r5)^2 + (r2 - y5)^2, # eq5
(x3 - x4)^2 - 1800, # eq6
-(r5 + 45/2)^2 + (x3 - x5)^2 + (y5 - 45/2)^2, # eq7
-(r5 + 20)^2 + (-x4 + x5)^2 + (y5 - 20)^2, # eq8
]
end;
iniv = [big"120.0", 200, 70, 30, 20, 17, 17, 17]
res = nls(H, ini=iniv);
println(res);
(BigFloat[180.0000000000000000315639921488776459575236334065858559417549014857970348855221, 254.5584412271571087953793012664368158326051549772724874493636018118273440778069, 89.99999999999999999414137791862049647293969079952184651651057986232141304475634, 127.2792206135785543912891769702404571933059905375609423589882744147464141850234, 84.85281374238570292723843621648770921579775164950411289786217536675179950468641, 17.99999999999999999772191395059268200439910616460700693283485445518118759929732, 101.8233764908628435131618139128282843444860986198208175883681931129179867092681, 53.99999999999999999717741648049545461928635214270576638615330713361282330565839], true)
r1 = 180; x1 = 254.558; r2 = 90; x3 = 127.279; x4 = 84.8528; r5 = 18; x5 = 101.823; y5 = 54
丙円の直径 = 36
x1, x3, x4, x5 はそれぞれ 180√2, 90√2, 60√2, 72√2 である。
using Plots
function draw(more)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(r1, x1, r2, x3, x4, r5, x5, y5) = res[1]
(r3, r4) = (45, 40) .// 2
@printf("r1 = %g; x1 = %g; r2 = %g; x3 = %g; x4 = %g; r5 = %g; x5 = %g; y5 = %g\n", r1, x1, r2, x3, x4, r5, x5, y5)
@printf("丙円の直径 = %g\n", 2r5)
plot()
circle(x1, r1, r1)
circle(0, r2, r2, :blue)
circle(x3, r3, r3, :green)
circle(x4, r4, r4, :magenta)
circle(x5, y5, r5, :orange)
if more == true
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) / 3 # size[2] * fontsize * 2
point(x1, r1, " 大:r1,(x1,r1)", :red, :left, :vcenter)
point(0, r2, "小:r2, (0,r2)", :blue, :center, :vcenter)
point(x3, r3, " 甲:r3,(x3,r3)", :green, :left, :vcenter)
point(x4, r4, "乙:r4,(x4,r4) ", :magenta, :right, :bottom)
point(x5, y5, " 丙:r5,(x5,y5) ", :orange, :left, :bottom)
hline!([0], color=:black, lw=0.5)
vline!([0], color=:black, lw=0.5)
else
plot!(showaxis=false)
end
end;