算額(その1373)
四十 群馬県前橋市山王町 日枝神社 文政7年(1824)
群馬県和算研究会:群馬の算額,上武印刷株式会社,高崎市,1987年3月31日.
キーワード:楕円,等脚台形,最大面積
#Julia, #SymPy, #算額, #和算
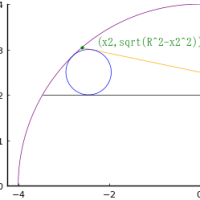
斜辺と上底が等しい(等斜と呼ぶ)等脚台形の中に楕円を容れる。等斜が 10 寸のとき,等脚台形の面積が最大になるときの楕円の長径はいかほどか。
等脚台形の,上底,下底,高さを 2j, 2k, h
楕円の長半径,短半径,中心座標を a, b, (0, b); b = h/2
楕円と等脚台形の斜辺の接点座標を (x0, y0)
とおき,以下の連立方程式を解く。
include("julia-source.txt");
# julia-source.txt ソース https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf
using SymPy
@syms j::positive, k::positive, h::positive,
S::positive, a::positive, b::positive,
x0::positive, y0::positive;
b = h/2
eq1 = (k - j)^2 + h^2 - (2j)^2
eq2 = x0^2/a^2 + (y0 - b)^2/b^2 - 1
eq3 = -b^2*x0/(a^2*(y0 - b)) + h/(k - j)
eq4 = y0/(k - x0) - h/(k - j);
k, a, x0, y0 は h, j を含む式になる。
res = solve([eq1, eq2, eq3, eq4], (k, a, x0, y0))[2] # 1 of 2
(j + sqrt(-h^2 + 4*j^2), sqrt(j)*sqrt(j + sqrt(-h^2 + 4*j^2)), 2*j*(h^2 - 2*j^2 + j*sqrt(-h^2 + 4*j^2))/h^2, (h^2 - 2*j^2 + j*sqrt(-h^2 + 4*j^2))/h)
等脚台形の面積は h*(4*j + 2*sqrt(-h^2 + 4*j^2))/2 で,等斜(=2j)が与えられれば,h だけの関数 h*(4j + 2sqrt(4*j^2 - h^2))/2 になる。
S = (2j + 2res[1])*h/2
S |> println
h*(4*j + 2*sqrt(-h^2 + 4*j^2))/2
等斜 = 10(j = 5)のとき,面積は下図のようになり,h が 9 前後のときに最大値をとる。
注:高さは 10 より大きくなれない。高さが 10 は極限状態であり,そのとき等脚台形は正方形になる。
pyplot(size=(300, 150), grid=false, aspectratio=:none, label="")
plot(S(j => 10/2), xlims=(0, 10), xlabel="h", ylabel="S")
面積 S が最大になるときの高さ h を求めるには,面積を表す式を h について微分し,その式が 0 になるときの h を求めればよい。
diff(S, h)
-h^2/sqrt(-h^2 + 4*j^2) + 2*j + sqrt(-h^2 + 4*j^2)
面積 S が最大になるときの h は √3j である。等斜が 10 寸のときは,h = 8.66025403784439 である。
h0 = solve(diff(S, h))[1]
h0[h] |> println
sqrt(3)*j
h = √3j のときの面積は 3*√3*j^2/2 である。
S(h => sqrt(Sym(3))*j) |> println
3*sqrt(3)*j^2
等斜が 10 寸のとき,面積は 3√3*5^2= 75√3/2 = 129.9038105676658 である。
要求されているのは楕円の長径である。
h = √3j のとき,長径は 2√2*j = √2*等斜= 14.1421356237310 である。
2res[2](h => j*√Sym(3)) |> simplify |> println
2*sqrt(2)*j
なお,h = √3j のとき,下底は 20 である。
2res[1](h => √Sym(3)j)(j => 10//2) |> println
20
面積は確かに (10 + 20) * 8.66025403784439 / 2 = 129.90381056766586 になる。
function draw(等斜, more)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
j = 等斜/2
h = √3j
(k, a, x0, y0) = (sqrt(100 - h^2) + 5, sqrt(5*sqrt(100 - h^2) + 25), 10*(h^2 + 5*sqrt(100 - h^2) - 50)/h^2, (h^2 + 5*sqrt(100 - h^2) - 50)/h)
S = h*(sqrt(100 - h^2) + 10)/2
b = h/2
@printf("等斜(上底)が %g,下底が %g のとき,楕円の長径は %g である。\n", 等斜, 2k, 2a)
plot([k, j, -j, -k, k], [0, h, h, 0, 0], color=:red, lw=0.5)
ellipse(0, b, a, b, color=:blue)
if more == true
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(j, h, "(j,h)", :red, :right, :bottom, delta=delta)
point(k, 0, "k", :red, :left, :bottom, delta=delta, deltax=delta/2)
point(0, b, " b", :blue, :left, :vcenter)
point(0, 2b, " 2b", :blue, :left, :bottom, delta=delta)
point(x0, y0, "(x0,y0)", :blue, :left, :vcenter, deltax=2delta)
end
end;
draw(10, true)

























※コメント投稿者のブログIDはブログ作成者のみに通知されます