算額（その1372）

算額（その1372）

七十二 群馬県富岡市一ノ宮 貫前神社 嘉永2年(1849)
群馬県和算研究会:群馬の算額，上武印刷株式会社，高崎市，1987年3月31日.
キーワード：内接円，外円，個数
#Julia, #SymPy, #算額, #和算

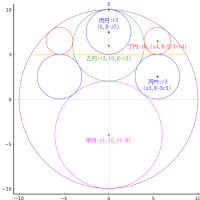
大円の中に互いに外接し合い大円に内接する等円を描く。大円と等円の直径が与えられたとき，等円の個数を求める術を述べよ。

大円と等円の半径を R, r，等円の個数を n とすれば，以下の関係式が成り立つ。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy
@syms R::positive, r::positive, n::positive
eq1 = asind(r/(R - r)) - 180/n
eq1 |> println

   180*asin(r/(R - r))/pi - 180/n

1.　等円の半径を求める

大円の半径と等円の個数を指定して等円の半径を求めるには，この関係式を等円の半径について解けばよい。

res = solve(eq1, r)[1]
res |> println

   R*sin(pi/n)/(sin(pi/n) + 1)

たとえば，外円の半径が 1，等円の個数が 8 のとき，等円の半径は以下により求めることができる（直径を与えれば直径が求まる）。

res(R => 1/2, n => 8).evalf() |> println
res(R => 1, n => 8).evalf() |> println

   0.138384326957078
   0.276768653914155

sin を計算するのはコンピュータにとっては何の苦もないことであるが，例えば電卓で計算するときには，近似式を使えばよい。
近似式 sin(x) ≈ x - x^3/6 + x^5/120 は小数点以下 5，6 桁まで正しい。

sin0(x) = x - x^3/6 + x^5/120

x = pi/n
(R*sin0(x)/(sin0(x) + 1))(R => 1/2, n => 8).evalf() |> println

   0.138384401530346

2.　等円の個数を求める

大円と等円の半径（直径）を指定して等円の個数を求めるには，前述の関係式を等円の個数について解く（必要ならば四捨五入する）。

res2 = solve(eq1, n)[1]
res2 |> println

   pi/asin(r/(R - r))

たとえば，外円，等円の半径が 0.5，0.138384326957078 のとき，等円の個数は 8 個である。

res2(R => 0.5, r => 0.138384326957078).evalf() |> println

   7.99999999999997

asin(arcsin) を計算するのはコンピュータにとっては何の苦もないことであるが，例えば電卓で計算するときには，近似式を使えばよい。
近似式 arcsin(x) ≈ x + x^3/6 + 3x^5/40 は小数点以下 4，5 桁まで正しい。

arcsin0(x) = x + x^3/6 + 3x^5/40

R = 1/2
r = 0.138384326957078
x = r/(R - r)
asin(x) |>  println
arcsin0(x) |> println

   0.39269908169872586
   0.392639425546951

等円の個数は，8.001215489793262 もしくは 7.997159214528561 になり，四捨五入すれば正しい答えになる。

pi/arcsin0(x) |> println
3.14/arcsin0(x) |> println

   8.001215489793262
   7.997159214528561

なお，「術」では，円周率*(大円の直径 - 等円の直径)/等円の直径 としている。これは上記近似式の最初の項だけを使用している。つまり arcsin(x) ≈ x としている。

大円の直径 = 1
等円の直径 = 0.276768653914155
円周率 = 3.14
円周率*(大円の直径 - 等円の直径)/等円の直径 |> println
円周率/(等円の直径/(大円の直径 - 等円の直径)) |> println

   8.205215419423654
   8.205215419423654

正確な asin を使おうが近似式を使おうが大円の直径，等円の直径が正確でなければ，計算結果は整数値からかなり外れることになるが，多くの場合は四捨五入すれば答えが得られるであろう。

function draw(R, r, more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   n = pi/asin(r/(R - r))
   n0 = 3.14/(r/(R - r))
   @printf("外円の直径が %g，等円の直径が %g のとき，等円の個数は %d である(近似値は %d)。\n", 2R, 2r, n, n0)
   plot()
   circle(0, 0, R)
   rotate(R - r, 0, r, angle=360/n, :blue)
   if more == true
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
   end
end;

R = 1/2
n = 13
r = R*sin(pi/n)/(sin(pi/n) + 1)
draw(R, r, true)