疑似乱数には手を出すな という格言があるくらいで(冗談)
乱数を作るのは難しい、疑似乱数だって難しい!
乱数は、次のサイコロの目が何?ってやつです(少し違うけど)
疑似乱数は、出る順番が決まっていたり、ある周期を持っていたりするやつです。
論文が出てたり、暗号表に使ってたり、パスワードの自動生成なんかに使ってるやつです。
3じゃない円周率だってある意味 乱数じゃん!
ネットで見つかる簡単な疑似乱数だと周期が短かっかたり、やたらに長いアセンブラだったり、理解できなかったり 笑
ということで、いいかげんな熟慮の元、作成してみました。
8ビット出力の乱数ですが、該出のPICで波形発生の6ビットのDA変換後のアナログ波形です。思った以上の長い周期になってるようです。周期を見つけられてません。
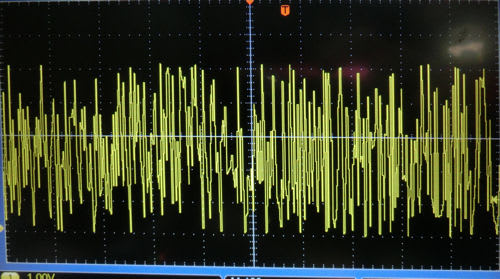
拡大 最大に振れているところはLSB2ビット分あればもっと上に行くでしょう(たぶん)

アセンブラです
CLRF M2
MOVLW D'3'
MOVWF T1
MOVLW D'7'
MOVWF T2
MOVLW D'11'
MOVWF T3
TT
RLF M2 なぜかここでデータをシフト 笑
MOVF M2,W
XORWF T1,0 T1,T2、T3でXOR
XORWF T2,0
XORWF T3,0
MOVWF M2
MOVWF PORTB ポートBの5ビット分のDA変換に出力 上の波形だよ
INCF T1,1 T1,T2、T3を+1してます
INCF T2,1
INCF T3,1
GOTO TT
10進数の3,7,11でXOR取って、次に3,7,11を1個づつ足していってXOR取って、その間にデータをシフトしてるってか!
乱数値を振幅にしましたが、正弦波波形の周期にしたいですね
お約束:疑似乱数として成立しているかなんて検証してないです。動物的感でアセンブラ組んじゃたので、そもそもの検証もしてないです。笑
著作権は放棄しますが、責任も放棄します。使う方は、自己責任でね!
追記:波形から周期を調べてみました。約740個で一周してます。256の3倍近いですね。もうちょっと工夫すれば周期が伸びるかもですね。
特徴ある波形のとこで一周期とし、その時間が1850μS、1パルスが2.5μSで計算しました。
追記の追記
サブルーチンでタイマを入れると繰り返しが途端に短くなります。キャリーフラグか? スタックとかめんどくさそう!要検討かな






































